O relógio marca 8 horas quantos graus

Dado um relógio marcando 8 horas, podemos ter as duas marcações de ângulos: \(a\) e \(b\)

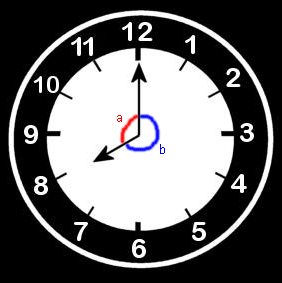
Relógio

Vamos analisar o ângulo \(b\):

Se o ponteiro das horas percorrer 12 horas, ele terá girado \(360°\). Mas, se ele andou até as 8h, basta fazer uma regra de 3 simples.

\[\eqalign{ & 12h - 360^\circ \cr & 8h - b }\]

\[12*b = 8*360^\circ\]

\[b = \dfrac{{360*8}}{{12}} = 30*8 = 240^\circ\]

Se analisássemos o problema pelo ângulo \(a\), seria o mesmo que o ponteiro das horas percorresse, no sentido inverso, 4h. Fazendo a regra de 3:

\[\eqalign{ & 12h - 360^\circ \cr & 4h - a }\]

\[12*a = 360*4\]

\[a = \dfrac{{360*4}}{{12}} = 30*4 = 120^\circ\]

Ou simplesmente bastaria subtrair \(240°\) (que corresponde ao ângulo \(b\)) dos \(360°\) totais

Então, \(a = 120^\circ\)

---

Os ângulos são: \(\boxed{a = 120^\circ }\) ou \(\boxed{b = 240^\circ }\)