
01-Um arame fino tem a forma de uma semicircunferência que está no primeiro e segundo
quadrante. O centro da semicircunferência está na origem e o raio é igual a 3. Encontre a
massa desse arame, utilizando a integral de linha sabendo que a função densidade é igual a
A) 108.
B) 54.
C) 27.
D) 0.
02-Para determinar o escoamento de um fluido ao longo de uma curva em um campo de
velocidades, podemos utilizar a integração de linha sobre campos vetoriais (campo de
velocidades). O escoamento ao longo do campo vetoriale a função movimento da partícula
é:
A) A posição inicial é (-3, 6) e a partícula está no ponto (-7, 20) quando t = 10 segundos.
B) A posição inicial é (5, -2) e a partícula está no ponto (-7, 20) quando t = 15 segundos.
C) A posição inicial é (1, 0) e a partícula está no ponto (-7, 20) quando t = 0 segundos.
D) A posição inicial é (3, 0) e a partícula está no ponto (-7, 20) quando t = 5 segundos.
03-Dada uma função escalar, o gradiente dessa função escalar é um campo vetorial cujas
componentes são as derivadas do campo escalar. Podemos afirmar que o gradiente da função
escalar de três variáveis
A) Somente a opção III está correta.
B) Somente a opção II está correta.
C) Somente a opção IV está correta.
D) Somente a opção I está correta.
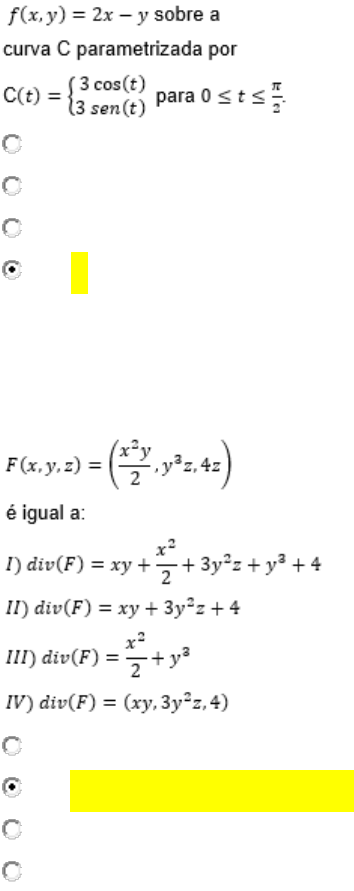
04-Considere a curva C definida pelo um quarto da circunferência de raio 3 contida no
primeiro quadrante e calcule a integral de linha da função
A) 0.
B) 3.
C) 6.
D) 9.
05-O divergente de uma função vetorial mede como é a dispersão do campo de vetores. No
caso de um fluido, o divergente pode indicar onde teria um sumidouro ou uma fonte
dependendo do sinal já que o divergente de uma função vetorial é um escalar. Com relação ao
divergente, podemos afirmar que o divergente da função vetorial
A) Somente a opção I está correta.
B) Somente a opção II está correta.
C) Somente a opção III está correta.
D) Somente a opção IV está correta.

06-Equações paramétricas são conjuntos de equações que representam uma curva, umas das
aplicações de equações paramétricas é descrever a trajetória de uma partícula, já que as
variáveis espaciais podem ser parametrizadas pelo tempo. Considerando uma reta paramétrica
que liga o ponto A (-1, 1) ao ponto B (3, 3), analise as opções a seguir e assinale a alternativa
CORRETA:
A) Somente a opção III está correta.
B) Somente a opção II está correta.
C) Somente a opção IV está correta.
D) Somente a opção I está correta.
07-Uma das aplicações de derivada na física é a velocidade de uma partícula, porém outra
aplicação muito utilizada de derivada é a reta tangente. Determine a reta tangente da função
vetorial:
A) A reta tangente é (2t, 3).
B) A reta tangente é 2t + 3.
C) A reta tangente é 2 + 3t.
D) A reta tangente é (2, 3t).
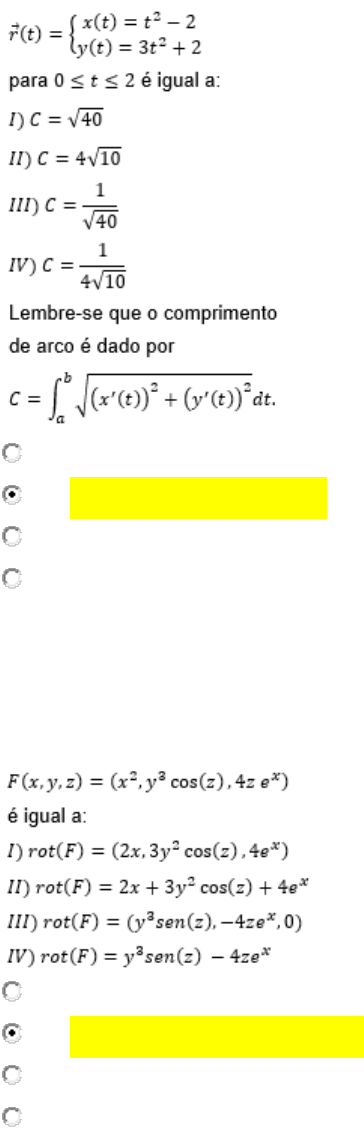
08-O comprimento do arco da curva
A) Somente a opção III é correta.
B) Somente a opção II é correta.
C) Somente a opção IV é correta.
D) Somente a opção I é correta.
09-O rotacional de uma função vetorial é um campo vetorial e calcula como os vetores de um
campo vetorial se aproximam (afastam) de um vetor normal. Com relação ao rotacional,
podemos afirmar que o rotacional da função vetorial
A) Somente a opção IV está correta.
B) Somente a opção III está correta.
C) Somente a opção II está correta.
D) Somente a opção I está correta.
10-Os campos vetoriais são altamente utilizados no estudo do comportamento de forças em
um espaço. Por isso, é importante sabermos encontrar propriedades desses campos vetoriais
através do cálculo de divergente e rotacional, por exemplo. Com relação ao campo vetorial,
assinale a alternativa CORRETA:

A) O campo rotacional é um vetor nulo.
B) O divergente do rotacional do campo vetorial é nulo.
C) O campo divergente é diferente de zero no ponto (0, 0).
D) O campo divergente é nulo em todos os pontos do plano.
01-Os campos vetoriais são altamente utilizados no estudo do comportamento de forças em
um espaço. Por isso, é importante sabermos encontrar propriedades desses campos vetoriais
através do cálculo de divergente e rotacional, por exemplo. Com relação ao campo vetorial,
assinale a alternativa CORRETA:
A) O campo divergente é diferente de zero no ponto (0, 0).
B) O divergente do rotacional do campo vetorial não é nulo.
C) O campo rotacional é um vetor nulo.
D) O campo divergente é nulo em todos os pontos do plano.
02-Um arame fino tem a forma de uma semicircunferência que está no primeiro e segundo
quadrante o centro da semicircunferência está na origem e raio é igual a 2. Utilizando a
integral de linha, temos que a massa desse arame, sabendo que a função densidade é
A) Somente a opção IV está correta.
B) Somente a opção II está correta.
C) Somente a opção I está correta.
D) Somente a opção III está correta.

03-Em muitas aplicações, precisamos calcular a derivada de uma função vetorial. O método é o
mesmo que aquele utilizado para derivar funções reais, basta apenas analisar cada uma das
componentes da função separadamente. Podemos afirmar que a derivada da função vetorial
A) Somente a opção III é correta.
B) Somente a opção II é correta.
C) Somente a opção IV é correta.
D) Somente a opção I é correta.
04Para modelar matematicamente situações físicas, utilizamos o conceito de funções.
Sabendo as propriedades da função, conseguimos encontrar respostas para o problema
modelado. No entanto, para encontrar as respostas, é importante conhecer os vários tipos de
funções e as suas propriedades. Com relação aos tipos de funções, podemos classificá-las
dependendo do seu conjunto domínio e do seu conjunto imagem. Com relação às funções e
seu domínio e imagem, associe os itens, utilizando o código a seguir:
I- Função vetorial de uma variável.
II- Função vetorial de n variáveis ou campos vetoriais.
III- Função escalar ou função real de n variáveis.
IV- Função real de uma variável.
Assinale a alternativa que apresenta a sequência CORRETA:
A) III - II - I - IV.
B) II - III - IV - I.
C) II - IV - I - III.
D) III - II - IV - I.

05-Uma partícula está se movendo segundo a função posição que depende do tempo. Então o
vetor tangente unitário da função posição
A) Somente a opção I é correta.
B) Somente a opção II é correta.
C) Somente a opção III é correta.
D) Somente a opção IV é correta.
06-Para determinar o escoamento de um fluido ao longo de uma curva em um campo de
velocidades, podemos utilizar a integração de linha sobre campos vetoriais (campo de
velocidades). O escoamento ao longo do campo vetorial
A) Somente a opção I está correta.
B) Somente a opção IV está correta.
C) Somente a opção III está correta.
D) Somente a opção II está correta.

01Um dos Teoremas mais utilizados para calcular integrais duplas e triplas é o Teorema de
Fubini, ele nos permite inverter a ordem de integração. Essa mudança na ordem de integração
pode em certas integrais diminuir a quantidade de cálculos necessários para a resolução.
Utilizando o Teorema de Fubini, concluímos que o valor da integral:
A) É igual a - 4.
B) É igual a 0.
C) É igual a - 3,5.
D) É igual a cos(3).
02-O Teorema de Stokes é muito similar ao Teorema de Green, a diferença entre eles é o
campo de vetores que estamos trabalhando, no Teorema de Green temos um campo de
vetores de duas variáveis, já no Teorema de Stokes temos um campo de vetores de três
variáveis, lembre-se que o Teorema de Stokes é:
A) Somente a opção I está correta.
B) Somente a opção II está correta.
C) Somente a opção IV está correta.
D) Somente a opção III está correta.
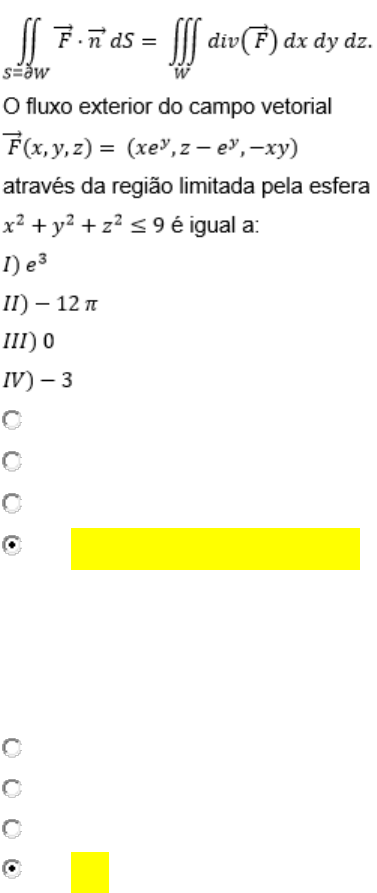
03-O teorema de Gauss muitas vezes é chamado de Teorema da divergência, pois transforma
uma integral de superfície de um campo vetorial em uma integral tripla do divergente desse
campo vetorial, ou seja, o Teorema de Gauss relaciona duas integrais:
A) Somente a opção II está correta.
B) Somente a opção IV está correta.
C) Somente a opção I está correta.
D) Somente a opção III está correta.
04-O momento de inércia de um corpo é o grau de dificuldade que o corpo tem de alterar o
seu estado de movimento. Podemos calcular o momento de inércia em torno do eixo x e do
eixo y. Determine o momento de inércia de um disco homogêneo com centro (0, 0) e raio igual
a 2 e com densidade f (x, y) = 2 em torno do eixo y:
A) 18 pi.
B) 12 pi.
C) 4 pi.
D) 8 pi.

05-Se uma partícula percorre um caminho, podemos utilizar a integral de linha para
determinar o trabalho realizado pelo campo de forças nessa partícula. Se a partícula percorre
no sentido anti-horário uma vez o círculo:
A) Somente a opção IV está correta.
B) Somente a opção III está correta.
C) Somente a opção I está correta.
D) Somente a opção II está correta.
06-Uma das aplicações de derivada na física é a velocidade de uma partícula, porém outra
aplicação muito utilizada de derivada é a reta tangente. Determine a reta tangente da função
vetorial:
A) A reta tangente é 5 + 2t.
B) A reta tangente é 2 + 5t.
C) A reta tangente é (-1 + 3t, 1 + 2t).
D) A reta tangente é (3 - t, 2 + t).
09-O trabalho realizado por um campo de forças sobre uma partícula é dado pela integral de
linha sobre uma curva. Utilizando o Teorema de Green podemos afirmar que o trabalho (W)
realizado por uma partícula ao longo do retângulo com orientação positiva e vértices (0, 0), (2,
0), (2, 3) e (0, 3) e campo de forças:
Prévia do material em texto
01-Um arame fino tem a forma de uma semicircunferência que está no primeiro e segundo quadrante. O centro da semicircunferência está na origem e o raio é igual a 3. Encontre a massa desse arame, utilizando a integral de linha sabendo que a função densidade é igual a A) 108. B) 54. C) 27. D) 0. 02-Para determinar o escoamento de um fluido ao longo de uma curva em um campo de velocidades, podemos utilizar a integração de linha sobre campos vetoriais (campo de velocidades). O escoamento ao longo do campo vetoriale a função movimento da partícula é: A) A posição inicial é (-3, 6) e a partícula está no ponto (-7, 20) quando t = 10 segundos. B) A posição inicial é (5, -2) e a partícula está no ponto (-7, 20) quando t = 15 segundos. C) A posição inicial é (1, 0) e a partícula está no ponto (-7, 20) quando t = 0 segundos. D) A posição inicial é (3, 0) e a partícula está no ponto (-7, 20) quando t = 5 segundos. 03-Dada uma função escalar, o gradiente dessa função escalar é um campo vetorial cujas componentes são as derivadas do campo escalar. Podemos afirmar que o gradiente da função escalar de três variáveis A) Somente a opção III está correta. B) Somente a opção II está correta. C) Somente a opção IV está correta. D) Somente a opção I está correta. 04-Considere a curva C definida pelo um quarto da circunferência de raio 3 contida no primeiro quadrante e calcule a integral de linha da função A) 0. B) 3. C) 6. D) 9. 05-O divergente de uma função vetorial mede como é a dispersão do campo de vetores. No caso de um fluido, o divergente pode indicar onde teria um sumidouro ou uma fonte dependendo do sinal já que o divergente de uma função vetorial é um escalar. Com relação ao divergente, podemos afirmar que o divergente da função vetorial A) Somente a opção I está correta. B) Somente a opção II está correta. C) Somente a opção III está correta. D) Somente a opção IV está correta. 06-Equações paramétricas são conjuntos de equações que representam uma curva, umas das aplicações de equações paramétricas é descrever a trajetória de uma partícula, já que as variáveis espaciais podem ser parametrizadas pelo tempo. Considerando uma reta paramétrica que liga o ponto A (-1, 1) ao ponto B (3, 3), analise as opções a seguir e assinale a alternativa CORRETA: A) Somente a opção III está correta. B) Somente a opção II está correta. C) Somente a opção IV está correta. D) Somente a opção I está correta. 07-Uma das aplicações de derivada na física é a velocidade de uma partícula, porém outra aplicação muito utilizada de derivada é a reta tangente. Determine a reta tangente da função vetorial: A) A reta tangente é (2t, 3). B) A reta tangente é 2t + 3. C) A reta tangente é 2 + 3t. D) A reta tangente é (2, 3t). 08-O comprimento do arco da curva A) Somente a opção III é correta. B) Somente a opção II é correta. C) Somente a opção IV é correta. D) Somente a opção I é correta. 09-O rotacional de uma função vetorial é um campo vetorial e calcula como os vetores de um campo vetorial se aproximam (afastam) de um vetor normal. Com relação ao rotacional, podemos afirmar que o rotacional da função vetorial A) Somente a opção IV está correta. B) Somente a opção III está correta. C) Somente a opção II está correta. D) Somente a opção I está correta. 10-Os campos vetoriais são altamente utilizados no estudo do comportamento de forças em um espaço. Por isso, é importante sabermos encontrar propriedades desses campos vetoriais através do cálculo de divergente e rotacional, por exemplo. Com relação ao campo vetorial, assinale a alternativa CORRETA: A) O campo rotacional é um vetor nulo. B) O divergente do rotacional do campo vetorial é nulo. C) O campo divergente é diferente de zero no ponto (0, 0). D) O campo divergente é nulo em todos os pontos do plano. 01-Os campos vetoriais são altamente utilizados no estudo do comportamento de forças em um espaço. Por isso, é importante sabermos encontrar propriedades desses campos vetoriais através do cálculo de divergente e rotacional, por exemplo. Com relação ao campo vetorial, assinale a alternativa CORRETA: A) O campo divergente é diferente de zero no ponto (0, 0). B) O divergente do rotacional do campo vetorial não é nulo. C) O campo rotacional é um vetor nulo. D) O campo divergente é nulo em todos os pontos do plano. 02-Um arame fino tem a forma de uma semicircunferência que está no primeiro e segundo quadrante o centro da semicircunferência está na origem e raio é igual a 2. Utilizando a integral de linha, temos que a massa desse arame, sabendo que a função densidade é A) Somente a opção IV está correta. B) Somente a opção II está correta. C) Somente a opção I está correta. D) Somente a opção III está correta. 03-Em muitas aplicações, precisamos calcular a derivada de uma função vetorial. O método é o mesmo que aquele utilizado para derivar funções reais, basta apenas analisar cada uma das componentes da função separadamente. Podemos afirmar que a derivada da função vetorial A) Somente a opção III é correta. B) Somente a opção II é correta. C) Somente a opção IV é correta. D) Somente a opção I é correta. 04Para modelar matematicamente situações físicas, utilizamos o conceito de funções. Sabendo as propriedades da função, conseguimos encontrar respostas para o problema modelado. No entanto, para encontrar as respostas, é importante conhecer os vários tipos de funções e as suas propriedades. Com relação aos tipos de funções, podemos classificá-las dependendo do seu conjunto domínio e do seu conjunto imagem. Com relação às funções e seu domínio e imagem, associe os itens, utilizando o código a seguir: I- Função vetorial de uma variável. II- Função vetorial de n variáveis ou campos vetoriais. III- Função escalar ou função real de n variáveis. IV- Função real de uma variável. Assinale a alternativa que apresenta a sequência CORRETA: A) III - II - I - IV. B) II - III - IV - I. C) II - IV - I - III. D) III - II - IV - I. 05-Uma partícula está se movendo segundo a função posição que depende do tempo. Então o vetor tangente unitário da função posição A) Somente a opção I é correta. B) Somente a opção II é correta. C) Somente a opção III é correta. D) Somente a opção IV é correta. 06-Para determinar o escoamento de um fluido ao longo de uma curva em um campo de velocidades, podemos utilizar a integração de linha sobre campos vetoriais (campo de velocidades). O escoamento ao longo do campo vetorial A) Somente a opção I está correta. B) Somente a opção IV está correta. C) Somente a opção III está correta. D) Somente a opção II está correta. 01Um dos Teoremas mais utilizados para calcular integrais duplas e triplas é o Teorema de Fubini, ele nos permite inverter a ordem de integração. Essa mudança na ordem de integração pode em certas integrais diminuir a quantidade de cálculos necessários para a resolução. Utilizando o Teorema de Fubini, concluímos que o valor da integral: A) É igual a - 4. B) É igual a 0. C) É igual a - 3,5. D) É igual a cos(3). 02-O Teorema de Stokes é muito similar ao Teorema de Green, a diferença entre eles é o campo de vetores que estamos trabalhando, no Teorema de Green temos um campo de vetores de duas variáveis, já no Teorema de Stokes temos um campo de vetores de três variáveis, lembre-se que o Teorema de Stokes é: A) Somente a opção I está correta. B) Somente a opção II está correta. C) Somente a opção IV está correta. D) Somente a opção III está correta. 03-O teorema de Gauss muitas vezes é chamado de Teorema da divergência, pois transforma uma integralde superfície de um campo vetorial em uma integral tripla do divergente desse campo vetorial, ou seja, o Teorema de Gauss relaciona duas integrais: A) Somente a opção II está correta. B) Somente a opção IV está correta. C) Somente a opção I está correta. D) Somente a opção III está correta. 04-O momento de inércia de um corpo é o grau de dificuldade que o corpo tem de alterar o seu estado de movimento. Podemos calcular o momento de inércia em torno do eixo x e do eixo y. Determine o momento de inércia de um disco homogêneo com centro (0, 0) e raio igual a 2 e com densidade f (x, y) = 2 em torno do eixo y: A) 18 pi. B) 12 pi. C) 4 pi. D) 8 pi. 05-Se uma partícula percorre um caminho, podemos utilizar a integral de linha para determinar o trabalho realizado pelo campo de forças nessa partícula. Se a partícula percorre no sentido anti-horário uma vez o círculo: A) Somente a opção IV está correta. B) Somente a opção III está correta. C) Somente a opção I está correta. D) Somente a opção II está correta. 06-Uma das aplicações de derivada na física é a velocidade de uma partícula, porém outra aplicação muito utilizada de derivada é a reta tangente. Determine a reta tangente da função vetorial: A) A reta tangente é 5 + 2t. B) A reta tangente é 2 + 5t. C) A reta tangente é (-1 + 3t, 1 + 2t). D) A reta tangente é (3 - t, 2 + t). 09-O trabalho realizado por um campo de forças sobre uma partícula é dado pela integral de linha sobre uma curva. Utilizando o Teorema de Green podemos afirmar que o trabalho (W) realizado por uma partícula ao longo do retângulo com orientação positiva e vértices (0, 0), (2, 0), (2, 3) e (0, 3) e campo de forças: A) Somente a opção I está correta. B) Somente a opção II está correta. C) Somente a opção III está correta. D) Somente a opção IV está correta. 10-O centro de massa de um objeto é o ponto onde este objeto fica em equilíbrio, caso esse objeto seja homogêneo. Para determinar o centro de massa, precisamos também saber a massa do objeto. Determine a massa de uma lâmina triangular com vértices (0, 0), (1, 0) e (0, 2), sabendo que a função densidade é f (x, y) = 3 - x + 2y: A) 10 B) 4 C) 0 D) 5 11-(ENADE, 2011) Em um plano de coordenadas cartesianas xOy, representa-se uma praça de área P, que possui em seu interior um lago de área L, limitado por uma curva C fechada, suave, orientada no sentido contrário ao dos ponteiros de um relógio. Considere que, sobre o lago, atua um campo de forças F(x,y)=(-y, x). Supondo que T representa o trabalho realizado por F(x,y) para mover uma partícula uma vez ao longo da curva C e que, comparando-se apenas os valores numéricos das grandezas, a área não ocupada pelo lago é igual a T/2, conclui-se que: A) T=4L B) P=2T C) T=L D) P=T 12-(ENADE, 2011) A) I e III, apenas. B) II, apenas. C) I e II, apenas. D) III, apenas. 03-Um sistema de coordenadas esféricas relaciona um ponto do espaço com dois ângulos e uma distância, esse sistema de coordenadas é muito utilizado para calcular integrais triplas na qual a região é uma esfera ou parte de uma. Utilizando a mudança de variável esférica, podemos afirmar que a integral A) Somente a opção IV está correta. B) Somente a opção I está correta. C) Somente a opção III está correta. D) Somente a opção II está correta. 04-Usando o Teorema de Green, podemos determinar o trabalho realizado pelo campo de forças F sobre uma partícula que se move ao longo do caminho específico. Se a partícula começa no ponto (2, 0) e percorre o círculo de raio igual a 2, então o trabalho realizado pelo campo de forças A) Somente a opção IV está correta. B) Somente a opção III está correta. C) Somente a opção II está correta. D) Somente a opção I está correta. 05-Utilize o Teorema de Gauss para calcular o fluxo exterior através da região limitada pelos planos x = 0, x = 3, e pelo cilindro circular A) Somente a opção III está correta. B) Somente a opção IV está correta. C) Somente a opção I está correta. D) Somente a opção II está correta. 06-Uma partícula percorre um caminho retangular definido pelos pontos x = 0, x = 2, y = 1 e y = 2 sobre o plano z = x + y com orientação anti-horária. Utilize o Teorema de Stokes para calcular o trabalho realizado pelo campo vetorial A) 0. B) - 8. C) - 4. D) 8. 07-O centro de massa de um objeto é o ponto onde este objeto fica em equilíbrio, caso esse objeto seja homogêneo. Determine a coordenada x do centro de massa de uma lâmina triangular com vértices (0, 0), (1, 0) e (0, 2), sabendo que a função densidade é f (x, y) = 3 - x + 2y e que a massa do objeto é igual a m = 4: A) 7/24 B) 24/7 C) 6/7 D) 7/6 10-Se uma partícula percorre um caminho, podemos utilizar a integral de linha para determinar o trabalho realizado pelo campo de forças nessa partícula. Se a partícula começa no ponto (3,0), percorre ao longo do eixo: A) Somente a opção I está correta. B) Somente a opção III está correta. C) Somente a opção IV está correta. D) Somente a opção II está correta. 11-(ENADE, 2014) Deseja-se pintar a superfície externa e lateral de um monumento em forma de um paraboloide, que pode ser descrita pela equação z = x² + y², situada na região do espaço de coordenadas cartesianas (x, y, z) dada pela condição z <= 9. Os eixos coordenados estão dimensionados em metros e gasta-se um litro e meio de tinta a cada metro quadrado de área da superfície a ser pintada. A quantidade de tinta, em litros, necessária para se pintar a superfície lateral do monumento é dada pela integral dupla: A) Item D. B) Item A. C) Item C. D) Item B. 12-(ENADE, 2011) A) I e III, apenas. B) III, apenas. C) I e II, apenas. D) II, apenas. 09-Um dos Teoremas mais utilizados para calcular integrais duplas e triplas é o Teorema de Fubini, ele nos permite inverter a ordem de integração. Essa mudança na ordem de integração pode em certas integrais diminuir a quantidade de cálculos necessários para a resolução. Utilizando o Teorema de Fubini, concluímos que o valor da integral: A É igual a 0. B É igual a e. C É igual a 96. D É igual a 64. 01-Uma das aplicações de derivada na física é a velocidade de uma partícula, porém outra aplicação muito utilizada de derivada é a reta tangente. Determine a reta tangente da função vetorial: A) A reta tangente é (3 + 2t, 1 + t, 4 + 4t). B) A reta tangente é (2t + 3,1 + t, 8t). C) A reta tangente é 7 + 8t. D) A reta tangente é 8 + 7t. 02-Uma das aplicações de derivada na física é a velocidade de uma partícula, porém outra aplicação muito utilizada de derivada é a reta tangente. Determine a reta tangente da função vetorial: A) A reta tangente é (1, 3 + t, 2t). B) A reta tangente é 3 + 4t. C) A reta tangente é (t, 1 + 3t, 2). D) A reta tangente é 4 + 3t.




