
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE
CENTRO DE DESENVOLVIMENTO SUSTENTÁVEL DO SEMIÁRIDO
UNIDADE ACADÊMICA DE ENGENHARIA DE PRODUÇÃO
GRADUAÇÃO EM ENGENHARIA DE PRODUÇÃO
DISCIPLINA: FÍSICA EXPERIMENTAL
PROFESSOR: JOSÉ VANDERLAN LEITE DE OLIVEIRA
EQUIPE – TURMA 2
ANDRESSA SOARES DA SILVA
JOÁS GALDINO DE OLIVEIRA
JÚNIOR ALVES DE ARAÚJO
MAÍTALA ANDRÉIA ANDRADE ALVES DE SOUZA
MARIANE EMANUELLE PESSOA SANTOS
ASSOCIAÇÃO DE MOLAS EM SÉRIE E PARALELO
SUMÉ
2019
2
SUMÁRIO
1
INTRODUÇÃO.................................................................................................
3
2
OBJETIVOS......................................................................................................
3
3
FUNDAMENTAÇÃO TEÓRICA.....................................................................
3
4
MATERIAIS UTILIZADOS.............................................................................
5
5
PROCEDIMENTO EXPERIMENTAL.............................................................
6
6
RESULTADOS..................................................................................................
6
7
QUESTIONÁRIO E DISCUSSÕES..................................................................
7
8
CONSIDERAÇÕES FINAIS.............................................................................
13
REFERÊNCIAS BIBLIOGRÁFICAS.....................................................................
13

3
1 INTRODUÇÃO
O experimento realizado consiste em analisar as associações em série e em
paralelo de um sistema massa-mola, no qu al aplicou-se uma força
que resultou na
elongação do conjunto de molas. A partir da relação estabel ecida entre essas grandezas
calculou-se as constantes elásticas referentes as duas associações, por m eio de relações
matemáticas e interpretações gráficas dos dados obtidos durante o experimento.
2 OBJETIVOS
» Estudar o comportamento da elongação d e uma mola suspensa por um peso
pendurado em sua extremidade em associação em série e em paralelo;
» Determinar a sua constante elástica das associações em série e em paralelo;
» Verificar a lei de associações de molas em série e paralelo.
3 FUNDAMENTAÇÃO TEÓRICA
A Lei de Hooke descreve a força restauradora q ue existe em diversos sistemas
quando comprimidos ou distendidos. Qualquer material, sobre o qual atua uma for ça,
sofrerá uma deformação. Quando essa deformação for considerada pequena, diz-se que o
material está no regime elástico, ou seja, retorna à sua forma original quando a força que
a gerou cessa. Logo, a força r estauradora surge sempre no sentido de recuperar o formato
original do material, assim, por exemplo, uma mo la esticada ou comprimida irá retornar
ao seu comprimento original devido à ação dessa força restauradora (FREITAS, 2010) .
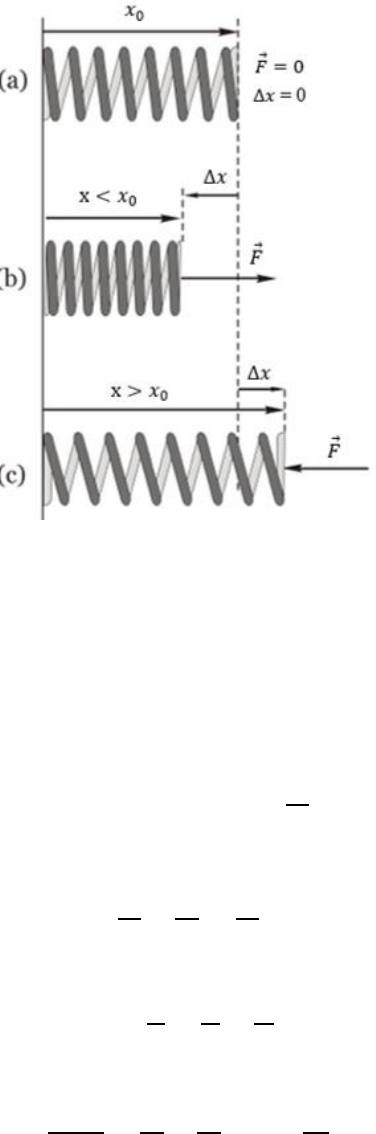
Ainda para o autor, a Figura 1(a) mostra uma mola com comprimento inicial .
Se esta for comprimida até um comprimento , a força
surge no sentido de
recuperar o compriment o original, como mostrado n a Figura 1(b). Caso a mola seja
esticada até um comprimento a força r estauradora
terá o sentido mostrado na
Figura 1(c). Em todas as situações descritas a força
é proporcional à d eformação ,
que é definida como . Portanto, como apresenta a Equação 1, n o regime
elástico há uma dependência linear entre a força
e a deformação .
(1)
4
Onde, k é a constante de proporcionalidade denominada de constante elástica da
mola. Essa equação formaliza a Lei de Hooke e o sinal negativo indica o fato de que a
força
tem sentido contrário a deformação .
Figura 1 – Mola: (a) natural, (b) comprimida e (c) esticada
Fonte: Freitas, (2010).
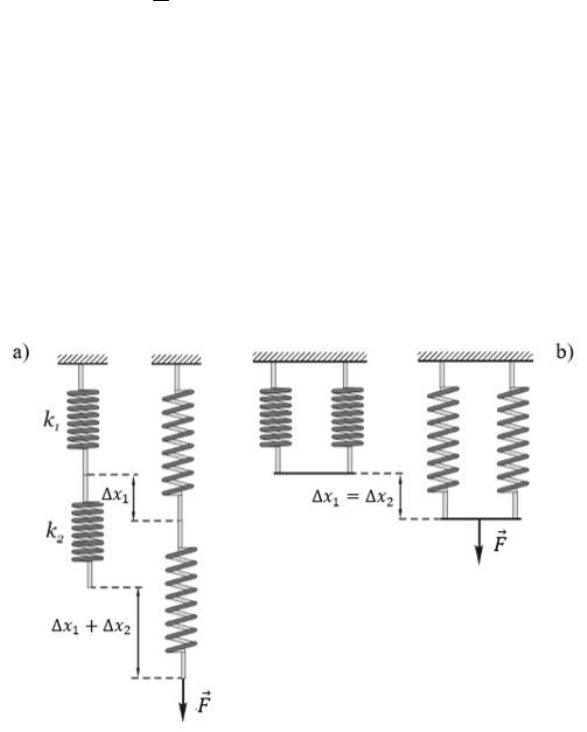
Conforme Calçada e S ampaio (1998), considerando duas molas ideais, como
mostra a Figura 2(a), de constantes
e
, associadas em série, e aplicando a
extremidade do conjunto uma força
, que atua igualmente em cada uma das molas
fazendo-as sofrer uma deformação, dada por:
Obtendo-se:
Que também pode ser expressa conforme a Equação 2:
(2)
Similarmente, para uma associação de n molas em série, tem-se:
5
Ainda conforme os autores, quando a associação é em paralelo, só tem int eresse
prático o caso de molas idênticas, isto é, molas que têm o mesmo comprimento natural e
a mesma constante elástica. Consi derando duas mol as idênticas, como m ostra a Figura
2(b), de constante elástica
, associadas em paralelo e presas a um mesmo suporte e a
uma barra de massa desprezível, no centro da qual é aplicada uma força
que é dividida
entre as duas molas, fazendo-as sofrer uma mesma deformação , tal que:
Associando a Lei de Hooke, obtém-se:
De modo geral, a Equação 3 pode ser ampliada se tiverem n molas idênticas
associadas em paralelo, sendo
a constante elástica de cada uma:
(3)
Figura 2 - (a) sistema com molas em série (b) sistema com molas em paralelo
Fonte: Freitas, (2010).
4 MATERIAIS UTILIZADOS
» Tripé de haste horizontal e vertical;
» Molas em séries e molas em paralelo;
» Massas de (10, 20, 50) gramas;
» Régua;
» Acoplador de massas.
6
5 PROCEDIMENTO EXPERIMENTAL
Medir o comprimento ini cial da associação das molas (L0) para cada caso e anotar
o valor obtido na tabela. Para estudar a elonga ção das molas em série e paralelo, prenda
uma massa na extremidade e medir o novo comprimento e anotar na tabela. Acrescentar
novas massas e r epetir as sequências, completando a tabela 1. Repetir o procedimento
anterior p ara a associação em paralelo, compl etando a tabela 2. Repetir o experimento
utilizando 3 molas.
6. RESULTADOS
Na primeira etapa do experimento realizou -se cinco medições dist intas da
elongação sofrid a por um sistema de mol as ass ociadas em série. Para efetuar cada
medição utilizou-se discos de diferentes massas. Inicialmente efetuou-s e o cálculo da
força, partindo do valor da massa e da gravidade local. Na sequência verificou-se o
comprimento inicial e o comprimento final apresentado pela mola após a aplicação da
força. Com esses dados calculou-se a deformação sofrida pel a mola, sua constante de
elasticidade e a média desse valor, como apresentado na Tabela 1.
Tabela 1 – Medidas de elongação da mola associada em série
Medida
Massa
(g)
Força
(10-3 N)
L0
(10-2 m)
Lf
(10-2 m)
∆L
(10-2 m)
F/∆L
(10-1 N/m)
Média
(10-1 N/m)
01
10
98
26,0
28,5
2,5
39,2
39,1
02
20
196
26,0
31,0
5,0
39,2
39,1
03
30
294
26,0
33,6
7,6
38,7
39,1
04
40
392
26,0
36,0
10,0
39,2
39,1
05
50
490
26,0
38,5
12,5
39,2
39,1
Na segunda parte do experimento realizou-se exatamente as etap as equivalentes
as descritas na p rimeira parte do experimento, no entanto, uti lizando-se um sistema de
molas associadas em paralelo. Os resultados obtidos são apresentados na Tabela 2.
Tabela 2 – Medidas de elongação da mola associada em paralelo
Medida
Massa
(g)
Força
(10-3 N)
L0
(10-2 m)
Lf
(10-2 m)
∆L
(10-2 m)
F/∆L
(10-1 N/m)
Média
(10-1 N/m)
01
50
490
12,0
14,1
2,1
233,3
233,3
02
100
980
12,0
16,2
4,2
233,3
233,3
03
150
1470
12,0
18,3
6,3
233,3
233,3
04
200
1960
12,0
20,4
8,4
233,3
233,3
05
250
2450
12,0
22,5
10,5
233,3
233,3

7
7 QUESTIONÁRIO E DISCUSSÕES
Para demonstrar o procedimento dos cálculos obtidos no experimento utilizou-se
como referência a medi da 1 realizada com a mola de associação em série. Os demais
valores foram obtidos repetindo o mesmo procedimento.
Questão 1
A partir das medições realizadas, como estruturado nas Tabelas 1 e 2, foram
calculadas as deformações sofridas pelas molas utilizadas no experimento.
Inicialmente foi medido o comprimento inicial da mola, ou seja, o comprimento
sem nenhuma interferência de deformação. Em seguida adicionou -se ao suporte acoplado
na extremidade d a mol a um disco com massa equivalente a 10g. Logo apó s, mediu -se o
comprimento final apresentado pela mola deformada. O cálculo da deformação sofrida
pela mola associada em série é obtido subtraindo -se a medida do comp rimento final do
inicial, conforme apresenta a Equação 4:
(4)
Questão 2
A constante elástica da mola foi c alculada utilizando a r elação entre a força
aplicada na mola e a variação do seu comprimento. Essa relação é estabelecida conforme
a Equação 5.
(5)
Em seguida, para calcu lar o valor médio das constantes elásticas da mol a
associada em série, utilizou-se a Equação 6.
(6)
8
Questão 3
Os dados referentes aos cálculos dos erros: absoluto, relativo e percentual para a
constante das associaçõe s das molas em série e em paralelo estão dispos tos conforme
apresenta a Tabela 3.
Tabela 3 – Erros absolutos, relativos e percentuais das molas
Medida
Erro associação em série
Erro associação em paralelo
Absoluto
(N/m)
Relativo
Percentual
Absoluto
(N/m)
Relativo
Percentual
1
0,01
0,00
0%
0,00
0,00
0%
2
0,01
0,00
0%
0,00
0,00
0%
3
0,04
0,01
1,0%
0,00
0,00
0%
4
0,01
0,00
0%
0,00
0,00
0%
5
0,01
0,00
0%
0,00
0,00
0%
Para encontrar os er ros relacionados à constante de elasticidade das molas
utilizou-se as seguintes equações:
O erro absoluto
(7)
N/m
O erro relativo
(8)
O erro percentual
(9)
Questão 4
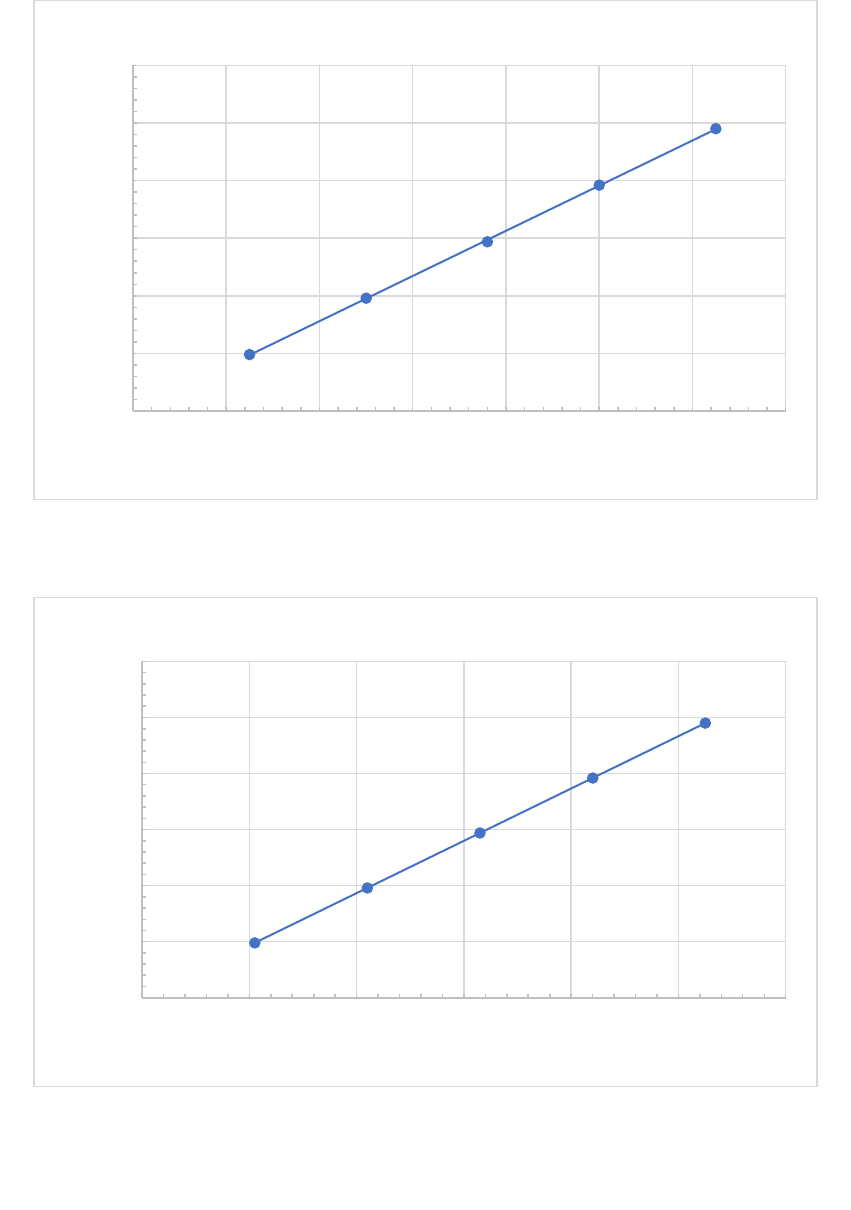
O Gráfico 1 apresenta a relação entre a forç a aplic ada na associação das molas em
série e a elongação sofri da por elas. Enquanto o Gráfico 2 mostra a relação referente a
associação das molas em paralelo.
9
Gráfico 1 - Relação entre a força e a elongação das molas associadas em série
Gráfico 2 - Relação entre a força e a elongação das molas associadas em paralelo
As deformações sofridas pelas molas são diretamente proporcionais à força a que
ela está sujeita, conforme apontam os Gráficos 1 e 2. Ao aumentar-se gradativamente a
intensidade da força aplicada as molas obtêm-se u ma variação gradativa no comprimento
apresentado por elas.
0
100
200
300
400
500
600
0246810 12 14
FORÇA
(10-3 N)
DEFORMAÇÃO (10-2 m)
FORÇA EM FUNÇÃO DA DEFORMAÇÃO
0
500
1000
1500
2000
2500
3000
0246810 12
FORÇA
(10-3 N)
DEFORMAÇÃO (10-2 m)
FORÇA EM FUNÇÃO D A DEFORMAÇÃO

10
Questão 5
Para cada gráfico apresentado acima, determinou-se o coeficiente angular da reta
por meio da Equação 10:
(10)
Para a mola em série utilizou-se os pontos P1 (5,196) e P2 (10, 392).
Para determinar o coeficiente da mola em paralelo repetiu -se o mesmo
procedimento usando os pontos P1 (2,1; 490) e P2 (6,3; 1470), obtendo o valor de
233,3 .
Os coeficientes angula res obtidos que representam a declividade da reta são
numericamente iguais às constantes elásticas das molas.
Questão 6
A resultante elástica foi uti lizada como base para demonstrar a expressão da
constante em paralelo (
) para as três molas.
Como
Demonstrando agora como obteve-se a expressão da constante em série (
) para
as duas molas. Tem-se que o alongamento total do conjunto será dado por:
Sabe-se também que:
Assim, utilizando as relações anteriores, temos:
Como, . Então:
Prévia do material em texto
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE DESENVOLVIMENTO SUSTENTÁVEL DO SEMIÁRIDO UNIDADE ACADÊMICA DE ENGENHARIA DE PRODUÇÃO GRADUAÇÃO EM ENGENHARIA DE PRODUÇÃO DISCIPLINA: FÍSICA EXPERIMENTAL PROFESSOR: JOSÉ VANDERLAN LEITE DE OLIVEIRA EQUIPE – TURMA 2 ANDRESSA SOARES DA SILVA JOÁS GALDINO DE OLIVEIRA JÚNIOR ALVES DE ARAÚJO MAÍTALA ANDRÉIA ANDRADE ALVES DE SOUZA MARIANE EMANUELLE PESSOA SANTOS ASSOCIAÇÃO DE MOLAS EM SÉRIE E PARALELO SUMÉ 2019 2 SUMÁRIO 1 INTRODUÇÃO................................................................................................. 3 2 OBJETIVOS...................................................................................................... 3 3 FUNDAMENTAÇÃO TEÓRICA..................................................................... 3 4 MATERIAIS UTILIZADOS............................................................................. 5 5 PROCEDIMENTO EXPERIMENTAL............................................................. 6 6 RESULTADOS.................................................................................................. 6 7 QUESTIONÁRIO E DISCUSSÕES.................................................................. 7 8 CONSIDERAÇÕES FINAIS............................................................................. 13 REFERÊNCIAS BIBLIOGRÁFICAS..................................................................... 13 3 1 INTRODUÇÃO O experimento realizado consiste em analisar as associações em série e em paralelo de um sistema massa-mola, no qual aplicou-se uma força �⃗� que resultou na elongação ∆𝐿 do conjunto de molas. A partir da relação estabelecida entre essas grandezas calculou-se as constantes elásticas referentes as duas associações, por meio de relações matemáticas e interpretações gráficas dos dados obtidos durante o experimento. 2 OBJETIVOS » Estudar o comportamento da elongação de uma mola suspensa por um peso pendurado em sua extremidade em associação em série e em paralelo; » Determinar a sua constante elástica das associações em série e em paralelo; » Verificar a lei de associações de molas em série e paralelo. 3 FUNDAMENTAÇÃO TEÓRICA A Lei de Hooke descreve a força restauradora que existe em diversos sistemas quando comprimidos ou distendidos. Qualquer material, sobre o qual atua uma força, sofrerá uma deformação. Quando essa deformação for considerada pequena, diz-se que o material está no regime elástico, ou seja, retorna à sua forma original quando a força que a gerou cessa. Logo, a força restauradora surge sempre no sentido de recuperar o formato original do material, assim, por exemplo, uma mola esticada ou comprimida irá retornar ao seu comprimento original devido à ação dessa força restauradora (FREITAS, 2010). Ainda para o autor, a Figura 1(a) mostra uma mola com comprimento inicial 𝑥0. Se esta for comprimida até um comprimento 𝑥 < 𝑥0 , a força �⃗� surge no sentido de recuperar o comprimento original, como mostrado na Figura 1(b). Caso a mola seja esticada até um comprimento 𝑥 > 𝑥0 a força restauradora �⃗� terá o sentido mostrado na Figura 1(c). Em todas as situações descritas a força �⃗� é proporcional à deformação ∆𝑥, que é definida como ∆𝑥 = 𝑥 − 𝑥0. Portanto, como apresenta a Equação 1, no regime elástico há uma dependência linear entre a força �⃗� e a deformação ∆x. �⃗� = −𝑘. ∆𝑥 (1) 4 Onde, k é a constante de proporcionalidade denominada de constante elástica da mola. Essa equação formaliza a Lei de Hooke e o sinal negativo indica o fato de que a força �⃗� tem sentido contrário a deformação ∆𝑥. Figura 1 – Mola: (a) natural, (b) comprimida e (c) esticada Fonte: Freitas, (2010). Conforme Calçada e Sampaio (1998), considerando duas molas ideais, como mostra a Figura 2(a), de constantes 𝐾1 e 𝐾2, associadas em série, e aplicando a extremidade do conjunto uma força �⃗�, que atua igualmente em cada uma das molas fazendo-as sofrer uma deformação, dada por: ∆𝑥𝑠 = ∆𝑥1 + ∆𝑥2 = 𝐹 𝑘𝑠 Obtendo-se: 𝐹 𝑘1 + 𝐹 𝑘2 = 𝐹 𝑘𝑠 Que também pode ser expressa conforme a Equação 2: 1 𝑘𝑠 = 1 𝑘1 + 1 𝑘2 (2) Similarmente, para uma associação de n molas em série, tem-se: 1 𝑘𝑠é𝑟𝑖𝑒 = 1 𝑘1 + 1 𝑘2 + ⋯ + 1 𝑘𝑛 5 Ainda conforme os autores, quando a associação é em paralelo, só tem interesse prático o caso de molas idênticas, isto é, molas que têm o mesmo comprimento natural e a mesma constante elástica. Considerando duas molas idênticas, como mostra a Figura 2(b), de constante elástica 𝐾1, associadas em paralelo e presas a um mesmo suporte e a uma barra de massa desprezível, no centro da qual é aplicada uma força �⃗� que é dividida entre as duas molas, fazendo-as sofrer uma mesma deformação∆𝑥, tal que: 𝐹 2 = 𝑘1. ∆𝑥 𝑜𝑢 𝐹 = 2𝑘1. ∆𝑥 Associando a Lei de Hooke, obtém-se: 𝑘. ∆𝑥 = 2𝑘1. ∆𝑥 𝑜𝑢 𝑘 = 2𝑘1 De modo geral, a Equação 3 pode ser ampliada se tiverem n molas idênticas associadas em paralelo, sendo 𝐾1 a constante elástica de cada uma: 𝑘 = 𝑛𝑘1 (3) Figura 2 - (a) sistema com molas em série (b) sistema com molas em paralelo Fonte: Freitas, (2010). 4 MATERIAIS UTILIZADOS » Tripé de haste horizontal e vertical; » Molas em séries e molas em paralelo; » Massas de (10, 20, 50) gramas; » Régua; » Acoplador de massas. 6 5 PROCEDIMENTO EXPERIMENTAL Medir o comprimento inicial da associação das molas (L0) para cada caso e anotar o valor obtido na tabela. Para estudar a elongação das molas em série e paralelo, prenda uma massa na extremidade e medir o novo comprimento e anotar na tabela. Acrescentar novas massas e repetir as sequências, completando a tabela 1. Repetir o procedimento anterior para a associação em paralelo, completando a tabela 2. Repetir o experimento utilizando 3 molas. 6. RESULTADOS Na primeira etapa do experimento realizou-se cinco medições distintas da elongação sofrida por um sistema de molas associadas em série. Para efetuar cada medição utilizou-se discos de diferentes massas. Inicialmente efetuou-se o cálculo da força, partindo do valor da massa e da gravidade local. Na sequência verificou-se o comprimento inicial e o comprimento final apresentado pela mola após a aplicação da força. Com esses dados calculou-se a deformação sofrida pela mola, sua constante de elasticidade e a média desse valor, como apresentado na Tabela 1. Tabela 1 – Medidas de elongação da mola associada em série Medida Massa (g) Força (10-3 N) L0 (10-2 m) Lf (10-2 m) ∆L (10-2 m) F/∆L (10-1 N/m) Média (10-1 N/m) 01 10 98 26,0 28,5 2,5 39,2 39,1 02 20 196 26,0 31,0 5,0 39,2 39,1 03 30 294 26,0 33,6 7,6 38,7 39,1 04 40 392 26,0 36,0 10,0 39,2 39,1 05 50 490 26,0 38,5 12,5 39,2 39,1 Na segunda parte do experimento realizou-se exatamente as etapas equivalentes as descritas na primeira parte do experimento, no entanto, utilizando-se um sistema de molas associadas em paralelo. Os resultados obtidos são apresentados na Tabela 2. Tabela 2 – Medidas de elongação da mola associada em paralelo Medida Massa (g) Força (10-3 N) L0 (10-2 m) Lf (10-2 m) ∆L (10-2 m) F/∆L (10-1 N/m) Média (10-1 N/m) 01 50 490 12,0 14,1 2,1 233,3 233,3 02 100 980 12,0 16,2 4,2 233,3 233,3 03 150 1470 12,0 18,3 6,3 233,3 233,3 04 200 1960 12,0 20,4 8,4 233,3 233,3 05 250 2450 12,0 22,5 10,5 233,3 233,3 7 7 QUESTIONÁRIO E DISCUSSÕES Para demonstrar o procedimento dos cálculos obtidos no experimento utilizou-se como referência a medida 1 realizada com a mola de associação em série. Os demais valores foram obtidosrepetindo o mesmo procedimento. Questão 1 A partir das medições realizadas, como estruturado nas Tabelas 1 e 2, foram calculadas as deformações sofridas pelas molas utilizadas no experimento. Inicialmente foi medido o comprimento inicial da mola, ou seja, o comprimento sem nenhuma interferência de deformação. Em seguida adicionou-se ao suporte acoplado na extremidade da mola um disco com massa equivalente a 10g. Logo após, mediu-se o comprimento final apresentado pela mola deformada. O cálculo da deformação sofrida pela mola associada em série é obtido subtraindo-se a medida do comprimento final do inicial, conforme apresenta a Equação 4: ∆𝐿 = 𝐿𝐹 − 𝐿𝑂 (4) ∆𝐿 = 28,5 − 26,0 ∆𝐿 = 2,5 𝑐𝑚 Questão 2 A constante elástica da mola foi calculada utilizando a relação entre a força aplicada na mola e a variação do seu comprimento. Essa relação é estabelecida conforme a Equação 5. 𝐾 = 𝐹 ∆𝐿 (5) 𝐾 = 98𝑥10−3 2,5𝑥10−2 = 39,2𝑥10−1 𝑁/𝑚 Em seguida, para calcular o valor médio das constantes elásticas da mola associada em série, utilizou-se a Equação 6. �̅� = ∑ 𝑦𝑖 𝑁 𝑁 𝑖=1 (6) �̅� = 39,1𝑥10−1 𝑁/𝑚 8 Questão 3 Os dados referentes aos cálculos dos erros: absoluto, relativo e percentual para a constante das associações das molas em série e em paralelo estão dispostos conforme apresenta a Tabela 3. Tabela 3 – Erros absolutos, relativos e percentuais das molas Medida Erro associação em série Erro associação em paralelo Absoluto (N/m) Relativo Percentual Absoluto (N/m) Relativo Percentual 1 0,01 0,00 0% 0,00 0,00 0% 2 0,01 0,00 0% 0,00 0,00 0% 3 0,04 0,01 1,0% 0,00 0,00 0% 4 0,01 0,00 0% 0,00 0,00 0% 5 0,01 0,00 0% 0,00 0,00 0% Para encontrar os erros relacionados à constante de elasticidade das molas utilizou-se as seguintes equações: O erro absoluto 𝐸𝐴 = |𝑣𝑎𝑙𝑜𝑟 𝑚𝑒𝑑𝑖𝑑𝑜 − 𝑣𝑎𝑙𝑜𝑟 𝑟𝑒𝑎𝑙| (7) 𝐸𝐴 = |3,92 − 3,91| = 0,01 N/m O erro relativo 𝐸𝑅 = | 𝐸𝐴 𝑣𝑎𝑙𝑜𝑟 𝑟𝑒𝑎𝑙 | (8) 𝐸𝑅 = | 0,01 3,91 | = 0,0025 𝐸𝑅 ≅ 0,00 O erro percentual 𝐸𝑃 = 𝐸𝑅 𝑥 100% (9) 𝐸𝑃 = 0,00 𝑥 100% = 0% Questão 4 O Gráfico 1 apresenta a relação entre a força aplicada na associação das molas em série e a elongação sofrida por elas. Enquanto o Gráfico 2 mostra a relação referente a associação das molas em paralelo. 9 Gráfico 1 - Relação entre a força e a elongação das molas associadas em série Gráfico 2 - Relação entre a força e a elongação das molas associadas em paralelo As deformações sofridas pelas molas são diretamente proporcionais à força a que ela está sujeita, conforme apontam os Gráficos 1 e 2. Ao aumentar-se gradativamente a intensidade da força aplicada as molas obtêm-se uma variação gradativa no comprimento apresentado por elas. 0 100 200 300 400 500 600 0 2 4 6 8 10 12 14 F O R Ç A ( 1 0 -3 N ) DEFORMAÇÃO (10-2 m) FORÇA EM FUNÇÃO DA DEFORMAÇÃO 0 500 1000 1500 2000 2500 3000 0 2 4 6 8 10 12 F O R Ç A ( 1 0 -3 N ) DEFORMAÇÃO (10-2 m) FORÇA EM FUNÇÃO DA DEFORMAÇÃO 10 Questão 5 Para cada gráfico apresentado acima, determinou-se o coeficiente angular da reta por meio da Equação 10: 𝑡𝑔𝛼 = ∆𝐹 ∆𝐿 (10) Para a mola em série utilizou-se os pontos P1 (5,196) e P2 (10, 392). 𝑡𝑔𝛼 = (392 − 196) 𝑥 10−3 (10 − 5) 𝑥 10−2 = 39,2 𝑥 10−1𝑁/𝑚 Para determinar o coeficiente da mola em paralelo repetiu-se o mesmo procedimento usando os pontos P1 (2,1; 490) e P2 (6,3; 1470), obtendo o valor de 233,3𝑥 10−1 𝑁/𝑚. Os coeficientes angulares obtidos que representam a declividade da reta são numericamente iguais às constantes elásticas das molas. Questão 6 A resultante elástica foi utilizada como base para demonstrar a expressão da constante em paralelo (𝐾𝑃) para as três molas. 𝑅𝑒𝑙 = 𝐹𝑒𝑙1 + 𝐹𝑒𝑙2 + 𝐹𝑒𝑙3 𝐾𝑒𝑞. 𝑋𝑇 = 𝐾1. 𝑋1 + 𝐾2. 𝑋2 + 𝐾3. 𝑋3 Como 𝑋𝑇 = 𝑋1 = 𝑋2 = 𝑋3 𝐾𝑒𝑞 = 𝐾1 + 𝐾2 + 𝐾3 Demonstrando agora como obteve-se a expressão da constante em série (𝐾𝑆) para as duas molas. Tem-se que o alongamento total do conjunto será dado por: 𝑋𝑇 = 𝑋1 + 𝑋2 Sabe-se também que: 𝑋𝑇 = 𝑅𝑒𝑙 𝐾𝑒𝑞 Assim, utilizando as relações anteriores, temos: 𝑅𝑒𝑙 𝐾𝑒𝑞 = 𝐹𝑒𝑙1 𝐾1 + 𝐹𝑒𝑙2 𝐾2 Como, 𝑅𝑒𝑙 = 𝐹𝑒𝑙1 = 𝐹𝑒𝑙2. Então: 1 𝐾𝑒𝑞 = 1 𝐾1 + 1 𝐾2 11 Questão 7 Para comparar os valores necessitou-se determinar de forma teórica as constantes elásticas referente a associação em série e em paralelo do experimento anterior. Logo, utilizou-se a Equação 2 para encontrar a constante elástica da mola associada em série: 1 𝐾𝑆 = 1 𝐾1 + 1 𝐾2 Com intuito de calcular a constante considera-se que K1 é aproximadamente igual a K2, onde o K utilizado foi obtido a partir do experimento anterior e é igual a 7,4 N/m. 1 𝐾𝑠 = 1 7,4 + 1 7,4 𝐾𝑆 = 3,7 𝑁/𝑚 Visando calcular a constante elástica em paralelo, utilizou-se as mesmas considerações do cálculo anterior. Para isso usou-se a Equação 11. 𝐾𝑃 = 𝐾1 + 𝐾2 + 𝐾3 (11) 𝐾𝑃 = 7,4 + 7,4 + 7,4 𝐾𝑃 = 22,2 𝑁/𝑚 As constantes encontradas neste experimento se aproximam dos valores obtidos acima. Portanto, observa-se que não houve discrepância. Questão 8 Através do Método do Mínimos Quadrados calculou-se a constante elástica para cada mola em série e em paralelo por meio da Equação 12. 𝑎 = 𝑁(∑ 𝑥𝑖.𝑦𝑖𝑁𝑖=1 )− (∑ 𝑥𝑖 𝑁 𝑖=1 ).(∑ 𝑦𝑖 𝑁 𝑖=1 ) 𝑁(∑ 𝑥𝑖2𝑁𝑖=1 )− (∑ 𝑥𝑖 𝑁 𝑖=1 ) 2 (12) O valor do coeficiente angular da reta apresentado no Gráfico 1: 𝑎 = 5 (12845 𝑥 10−5) − (37,6 𝑥 10−2). (1328 𝑥 10−3) 5 (345,26 𝑥 10−4) − (37,6 𝑥𝑥 10−4)2 = 39,2 𝑥 10−1𝑁/𝑚 Equação: 𝑦 = 3,92𝑥 12 O valor do coeficiente angular da reta obtida a partir do Gráfico 2: 𝑎 = 5 (56595 𝑥 10−5) − (31,5 𝑥 10−2). (7350 𝑥 10−3) 5 (242,55 𝑥 10−4) − (31,5 𝑥 10−2)2 = 233,3 𝑥 10−1𝑁/𝑚 Equação: 𝑦 = 23,33𝑥 Por se tratar de um experimento sobre a verificação da Lei de Hooke os Gráficos 1 e 2 tendem a passar pela origem, logo o valor de b (coeficiente linear) para ambos estará próximo a zero. Os valores referentes às constantes elásticas das molas em série e em paralelos se mostraram coerente, tendo em vista, que os resultados encontrados estão próximos das médias das constantes elásticas obtidas no experimento. Questão 9 Sim, pois a constante elástica da mola depende da natureza de fabricação do material, de suas dimensões e do número de espiras. No experimento de associação de molas em série observa-se que a constante elástica encontrada foi menor que a constante obtida no experimento executado anteriormente (verificação da Lei de Hooke) utilizando apenas uma mola, isso se deu pois a mola associada em série possui um maior número de espiras, dessa forma, conclui-se que ao aumentar o número de espiras de uma mola sua constante elástica irá diminuir. Questão 10 Provavelmente ocorreu o erro de observação ao medir o comprimento do fio. Esse tipo de erro é chamado de paralaxe. 13 8 CONSIDERAÇÕES FINAIS Finalizando o experimento prático sobre a associação de molas em série e em paralelo, concluiu-se que: » Com os dados experimentais foram determinadas as constantes elásticas para as molas associadas em série e em paralelo. » Nos métodos (mínimos quadrados, tangente e constante elástica equivalente emsérie e em paralelo) utilizados para calcular as constantes das molas, os valores encontrados foram próximos, não havendo discrepâncias, o que significa dizer que os erros cometidos na execução do experimento foram mínimos. » A constante encontrada para as molas associadas em paralelo é maior que a constante das molas associadas em série, como observa-se nas Tabelas 1 e 2, isso indica que as molas de associação em série se deformaram com uma maior facilidade. » Observa-se que na associação da mola em série o alongamento de uma das molas é independente do alongamento da outra. Enquanto que na associação em paralelo os alongamentos das molas são os mesmos. » As molas voltaram ao seu comprimento inicial devido à ação da força restauradora, obedecendo a Lei de Hooke. Dessa maneira, os objetivos propostos pelo experimento foram atingidos. REFERÊNCIAS BIBLIOGRÁFICAS CALÇADA, C. S.; SAMPAIO, J. L. Física Clássica – Dinâmica e Estática. 2ª ed. vol. 2. São Paulo: Atual, 1998. FREITAS, L. Lei de Hooke. Disponível em: http://www.ufjf.br/fisica/files/2010/03/06_Pratica6-Hooke.pdf. Acesso em: 04 nov. 2019. Roteiro de atividades da disciplina Laboratório de Física Experimental da UFCG – Campus Sumé, 2019.









