Funções: gráfico, domínio,
imagem, contradomínio e
crescimento
05
Aula
2A
Matemática
1
No plano cartesiano, a cada ponto associamos um
par ordenado e, reciprocamente, a cada par ordenado
existe em correspondência um ponto. Essa associação
nos permite representar o comportamento gráfico de
uma função.
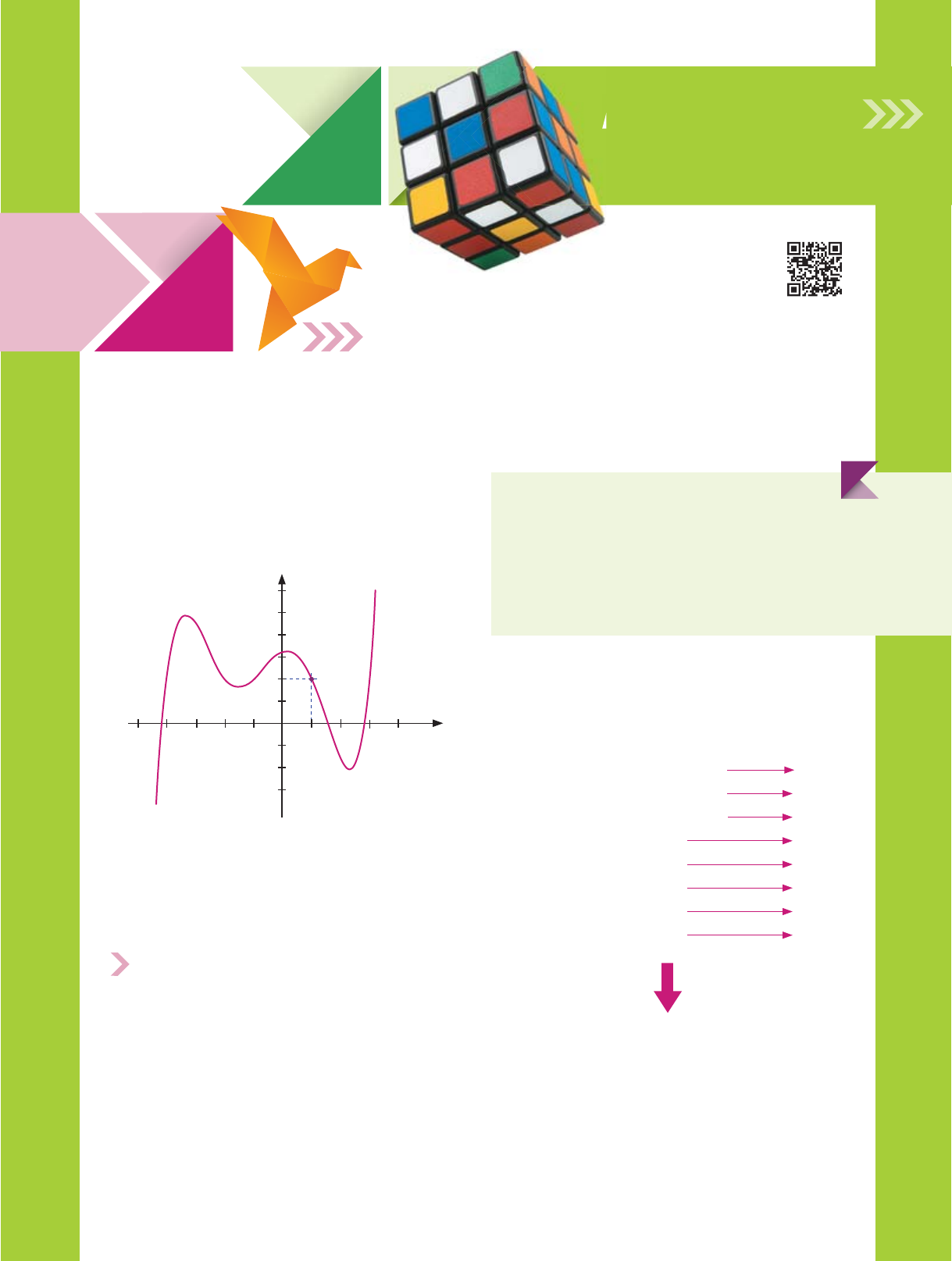
y
f
P
2
1x
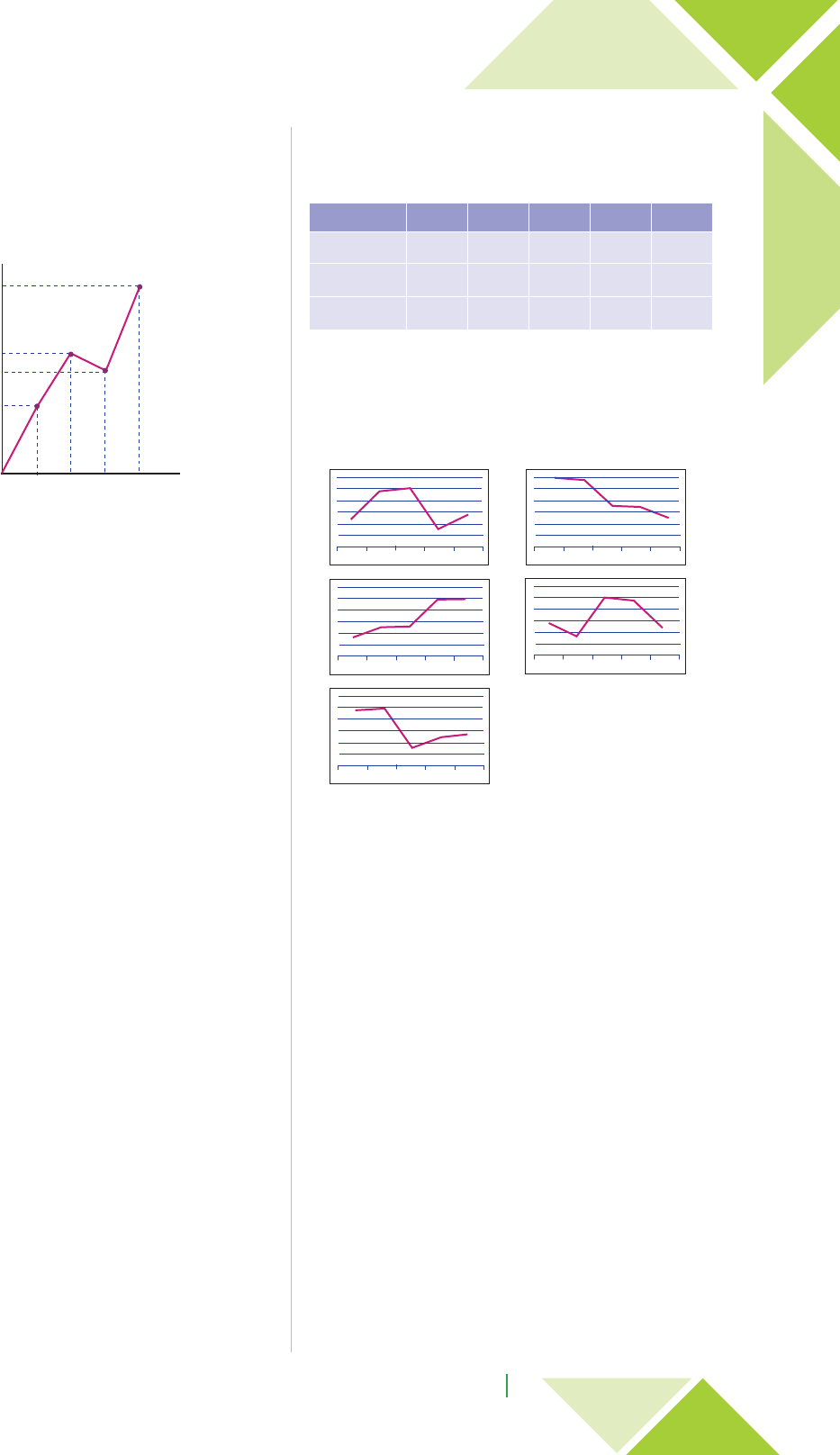
No gráfico acima, o ponto P(1; 2) pertencente à curva
é tal que f(1) = 2, isto é, 2 é a imagem de 1 por meio da
função f. A análise gráfica de uma função permite-nos
compreender como as grandezas que definem a função
estão relacionadas.
Gráfico de uma função
Como numa função y = f(x) associamos valores
de duas grandezas, podemos utilizar essa ideia para
“visualizarmos” o comportamento de uma função.
Assim, ficará mais evidente a relação existente entre as
variáveis envolvidas na função. A construção do gráfico
de uma função a par tir de sua lei de formação segue as
seguintes etapas:
• Atribuem-se valores do domínio da função à
variável x;
• Obtêm-se valores para a variável dependente y;
• A cada par ordenado (x; y) localiza-se um ponto no
plano cartesiano;
• Ligam-se convenientemente os pontos para obter-
-se o gráfico.
Exemplo:
Vamos construir, no plano car tesiano, o gráfico
da função que relaciona x e y, conforme a sentença
y = f(x) = 2x, sendo x e y números reais.
Atribuem-se valores para x, calculando
os correspondentes valores para y.
x = – 3 → y = f(– 3) = 2 ∙ (– 3) = – 6 (– 3; – 6)
x = – 2 → y = f(– 2) = 2 ∙ (– 2) = – 4 (– 2; – 4)
x = – 1 → y = f(– 1) = 2 ∙ (– 1) = – 2 (– 1; – 2)
x = 0 → y = f(0) = 2 ∙ 0 = 0 (0; 0)
x = 1 → y = f(1) = 2 ∙ 1 = 2 (1; 2)
x = 2 → y = f(2) = 2 ∙ 2 = 4 (2; 4)
x = 3 → y = f(3) = 2 ∙ 3 = 6 (3; 6)
x = 4 → y = f(4) = 2 ∙ 4 = 8 (4; 8)
2Extensivo Terceirão
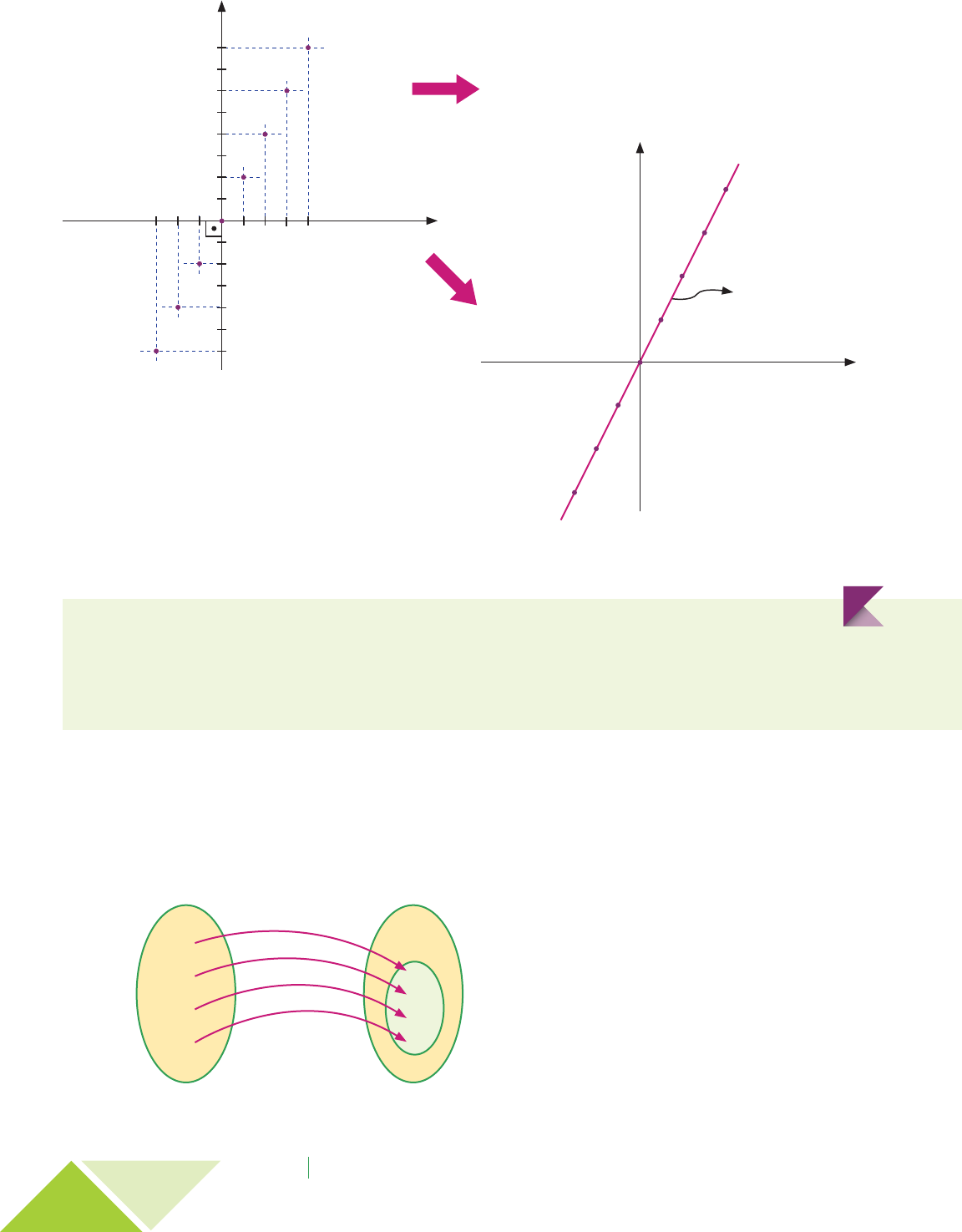
Localizamos os pontos correspondentes a esses
pares ordenados no plano cartesiano, obtendo
assim apenas alguns pontos.
Os pontos devem ser ligados convenientemente confor-
me o domínio da função. Se o domínio é o conjunto dos
números reais, ligamos os pontos de forma contínua.
y
0
2
x
8
7
6
5
4
3
1
–1–3 –2 1 2 43
–1
–3
–2
–6
–5
–4
y
x
y = 2x
• Domínio é o conjunto formado por todos os valores da variável independente x;
Representamos por D(f )
• Imagem é o conjunto formado por todos os valores da variável dependente y, tal que y = f(x);
Representamos por Im(f )
• Contradomínio é o conjunto B correspondente à f: A o B
Observações:
1. Quando escrevemos uma função f: A o B, o conjunto A é denominado domínio da função e é representado por
D(f ). Já o conjunto B é o contradomínio e representamos por CD(f ).
2. Caso não sejam indicados, convencionamos que o domínio e o contradomínio de uma função é o conjunto dos
números reais \.
Conforme diagrama ao lado, temos:
•Domínio:
D(f ) = A = {– 1; 0; 1; 2}
•Imagem:
Im(f ) = {7; 8; 9; 10}
•Contradomínio:
CD(f ) = B = {5; 6; 7; 8; 9; 10; 11}
AB
– 1
0
1
2
5
6
7
8
9
10
11
f : A o B
Aula 05
3
Matemática 2A
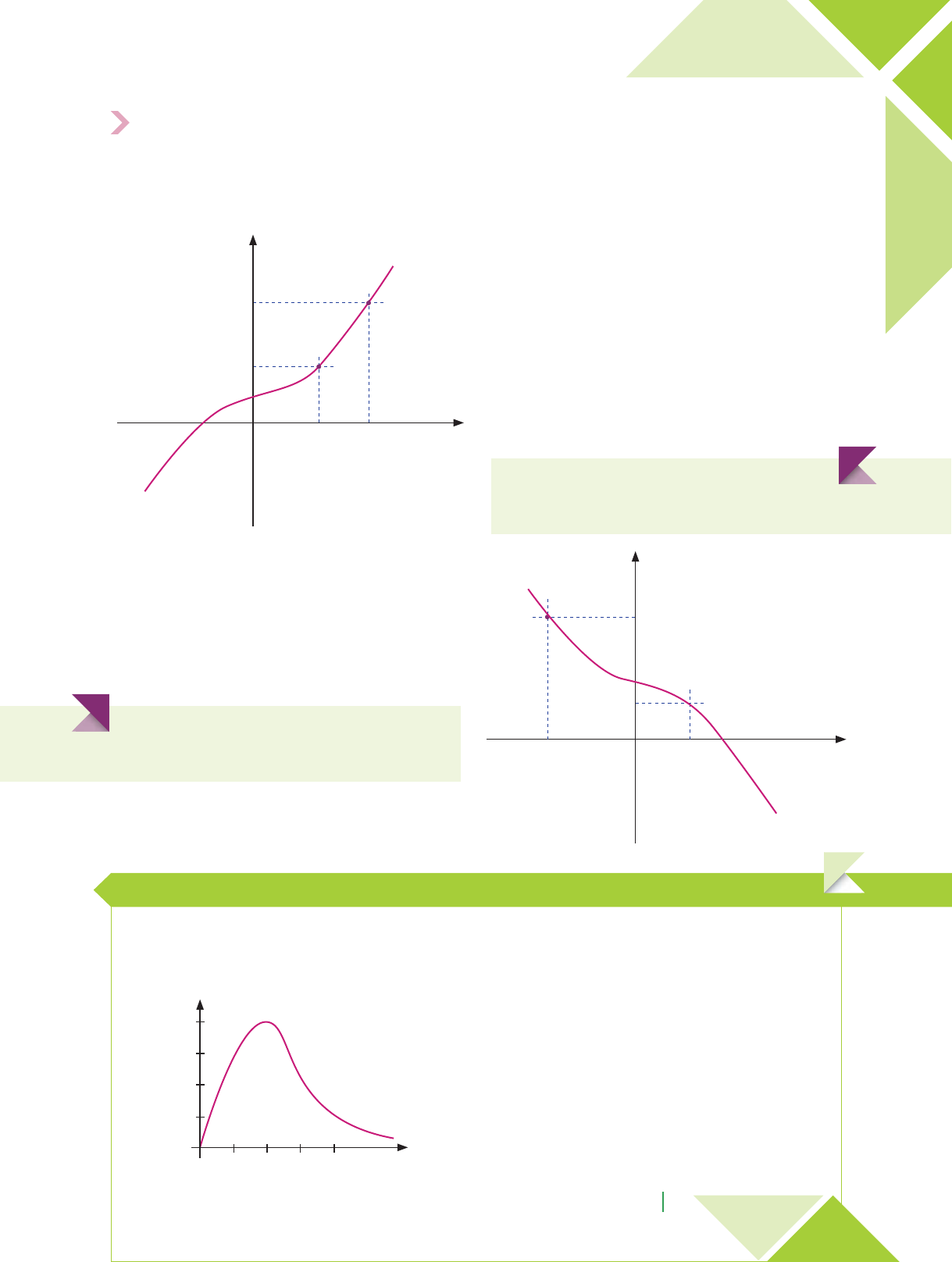
Crescimento de uma função
No estudo de algumas funções, observamos que, sempre que aumentamos o valor da variável independente x, o
valor da variável dependente y também aumenta. Essas funções são ditas crescentes. Também existem funções que,
sempre quando aumentamos o valor da variável indepente x, o valor da variável dependente y diminui. Tais funções
são denominadas funções decrescentes.
01. (UFPR) – Um estudo feito com cer to tipo de bactérias detectou que, no decorrer de uma infecção, a quantidade
dessas bactérias no corpo de um paciente varia aproximadamente segundo uma função q(t) que fornece o número
de bactérias em milhares por mm3 de sangue no instante t. O gráfico da função q(t) encontra-se esboçado abaixo.
O tempo é medido em horas, e o instante t = 0 corresponde ao momento do contágio.
00 4824 t
1
4
3
2
q(t)
Com base nessas informações, considere as seguintes afir-
mações:
I. A função q(t) é crescente no intervalo [0; 48]
II. A quantidade máxima de bactérias é atingida 24 horas
após o contágio, aproximadamente.
III. 60 horas após o contágio, a quantidade de bactérias está
abaixo de 1500 por mm3.
Situações para resolver
•Gráfico de uma função decrescente
Uma função f é dita decrescente quando para todo
x1 < x2, pertencentes ao domínio da função, tem-se
f(x1) > f(x2).
y
f(x1)
f(x2)
xx1x2
•Gráfico de uma função crescente
Uma função f é dita crescente quando para todo
x1 < x2, pertencentes ao domínio da função, tem-se
f(x1) < f(x2).
y
f(x1)
f(x2)
xx1x2
Assinale a alternativa correta.
a) Somente as afirmativas I e II são verdadeiras.
c) Somente as afirmativas II e III são verdadeiras.
e) Somente a afirmativa III é verdadeira.
b) Somente as afirmativas I e III são verdadeiras.
d) Somente a afirmativa I é verdadeira.
02. (UFSCAR – SP) – Para estimar a área da figura ABDO (sombreada no
desenho), onde a cur va AB é par te da representação gráfica da função
f(x) = 2x, João demarcou o retângulo OCBD e, em seguida, usou um
programa de computador que “plota” pontos aleatoriamente no interior
desse retângulo. Sabendo que dos 1000 pontos “plotados” apenas 540
ficaram no interior da figura ABDO, a área estimada dessa figura, em uni-
dades de área, é igual a
a) 4,32 b) 4,26
c) 3,92 d) 3,84
e) 3,52
CB
A
Ox
y
D = 2
4Extensivo Terceirão
Testes
Assimilação
05.01. O diagrama abaixo representa uma função f de A em B. O domínio, a imagem e f(4) são, respectivamente:
AB
0
1
2
3
4
5
7
9
11
13
15
17
a) {0,1,2,3,4}, {5,7,9,11,13,15,17} e 7 b) {5,7,9,11,13,15,17},{ 0,1,2,3,4,5} e 9
c) {0,1,2,3,4}, {5,7,13,15} e 7 d) {5,7,13,15}, {5,7,9,11,13,15,17} e 15
e) {0,1,2,3,4}, {9,11,17} e 7
Aula 05
5
Matemática 2A
O valor da expressão E = f (3) + f (2 ) + f
51
3
⎛
⎝
⎜⎞
⎠
⎟ per tence
ao conjunto
a) {x ∈ IR / –2 < x ≤ –1}
b) {x ∈ IR/ –1 < x ≤ 0}
c) {x ∈ IR / 1 < x ≤ 2}
d) {x ∈ IR / 0 < x ≤ 1}
Aperfeiçoamento
05.05. Dados os conjuntos A = {–3, –2, –1, 0, 1} e
B = { –8, –7, –6, –5, –4, –3, –2, –1, 0, 1 ,2} , considere a função
f de A em B, definida por f(x) = 2x – 2. Determine:
a) O domínio de f
b) O contradomínio de f
c) A imagem de f
d) x sendo f(x) = –4
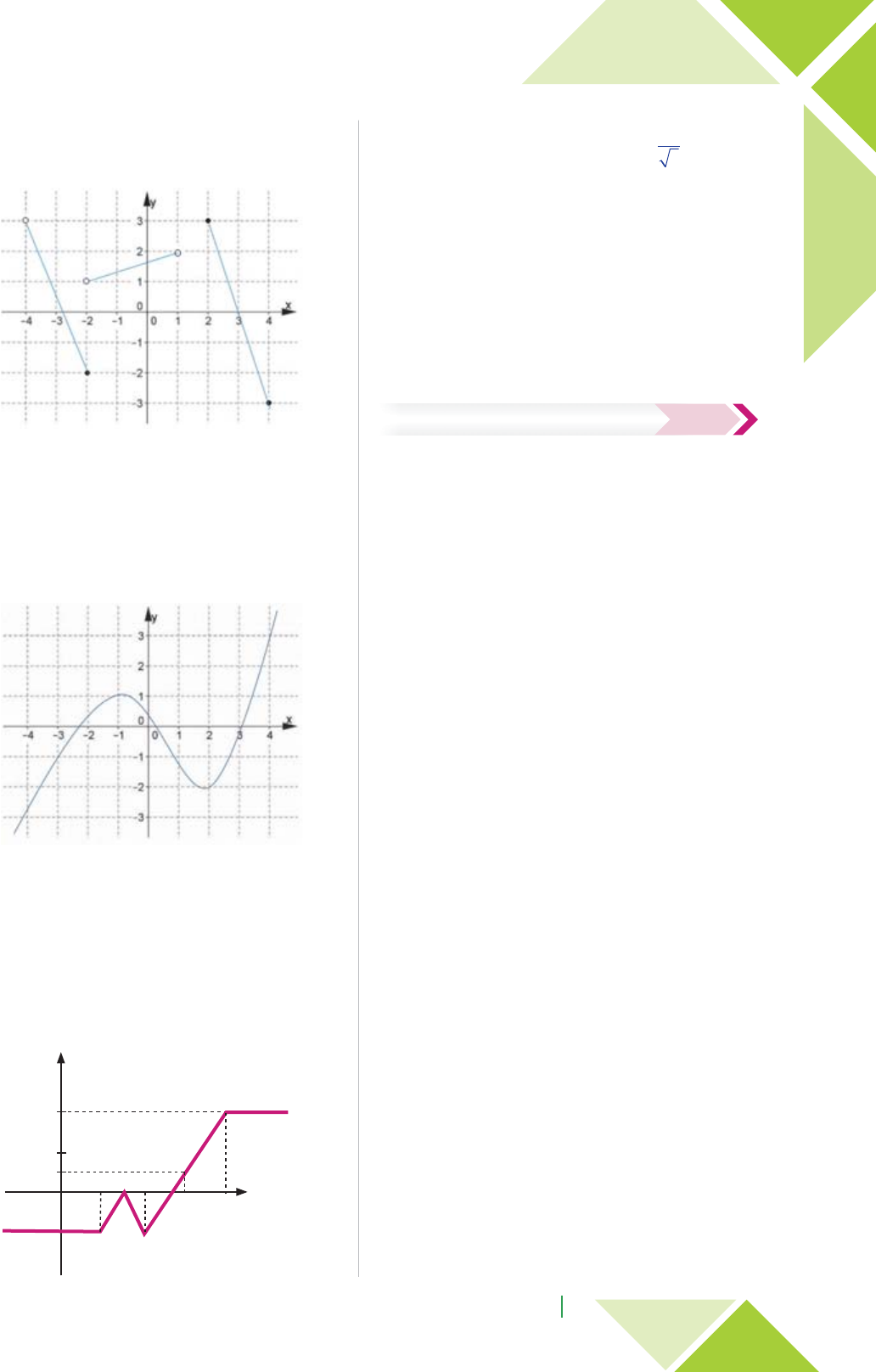
05.02. Coloque V ou F, conforme as afirmações abaixo
sejam verdadeiras ou falsas, respectivamente, em relação
ao gráfico abaixo:
( ) f(–2) = 1
( ) f( 3) = 0
( ) f(1) = 2
( ) f(0) > 1
( ) D om(f ) = ]-4:4]
( ) I m(f ) = [–3, 3]
05.03. O conjunto imagem da função abaixo, é:
a) [– 4: 4]
b) ]– 4; 4[
c) [– 3; 3]
d) ]– 3; 3[
e) IR
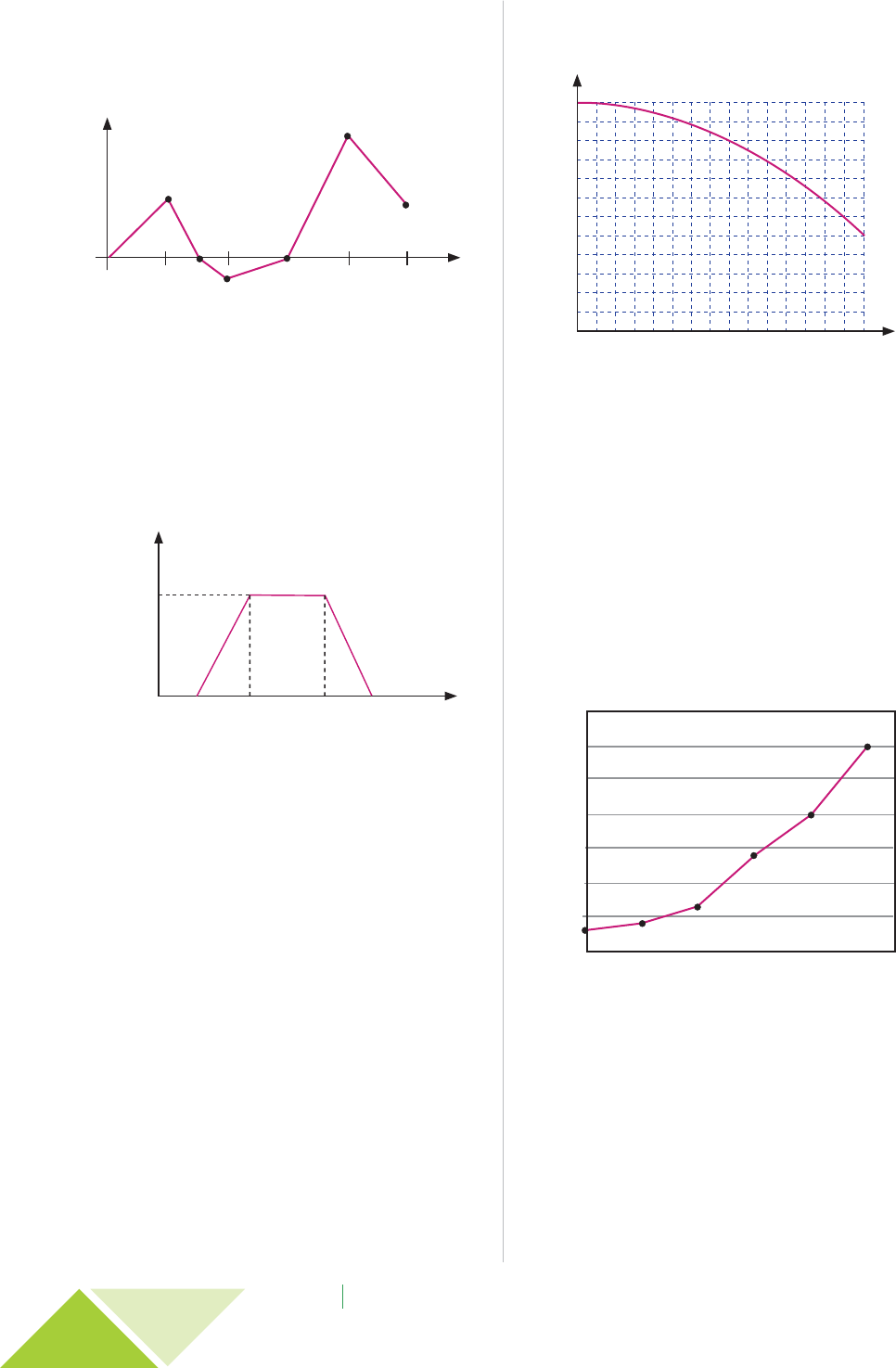
05.04. (CEFET – MG) – Na figura, está representado o gráfico
da função f : R → R, tal que f (x) = y.
y
2
1
12
34
–1
0
0,5
f
x
6Extensivo Terceirão
05.06. (UFPE) – O gráfico a seguir fornece o perfil do lucro
de uma empresa agrícola ao longo do tempo, sendo o ano
zero, o ano de sua fundação. Analisando o gráfico, julgue as
afirmativas:
10
LUCRO
15 20 255 ANO
( ) 10 foi o único ano em que ela foi deficitária.
( ) 20 foi o ano de maior lucro.
( ) 25 foi um ano deficitário.
( ) 15 foi um ano de lucro.
( ) 5 foi o ano de maior lucro no período que vai da fun-
dação até o ano 15.
05.07. (CEFET – SC) – A velocidade de um carro é medida
durante 30s. O gráfico a seguir mostra a variação dessa ve-
locidade v (em Km/h) ao longo do tempo t (em s).
60
V (km/h)
5 12 20 25 30 t(s)
Leia atentamente as afirmativas abaixo:
I. O automóvel permaneceu parado nos primeiros 5 se-
gundos analisados.
II. Entre os instantes 12s e 20s a velocidade do automóvel
variou.
III. O carro não se movimentou entre os instantes 12s e 20s.
IV. A velocidade que o carro atingiu no instante 10s voltou
a ser atingida entre os instantes 20s e 25s.
Estão CORRETAS apenas as afirmativas:
a) I, II e IV.
b) II e IV.
c) I e IV.
d) I, III e IV.
e) III e IV.
05.08. (IBMEC – SP) – Na figura está representado o preço
de um console de video game, em função do tempo decor-
rido desde o seu lançamento.
2,75
3,00
2,50
2,25
2,00
1,75
1,50
1,25
1,00
0,75
0,50
0,25
001512963
t (meses)
p (milhares de reais)
O preço do aparelho será menor do que 50% do valor de
lançamento a partir do
a) 6 .
o mês. b) 8 .
o mês. c) 10.
o mês.
d) 12 .
o mês. e) 14 .
o mês.
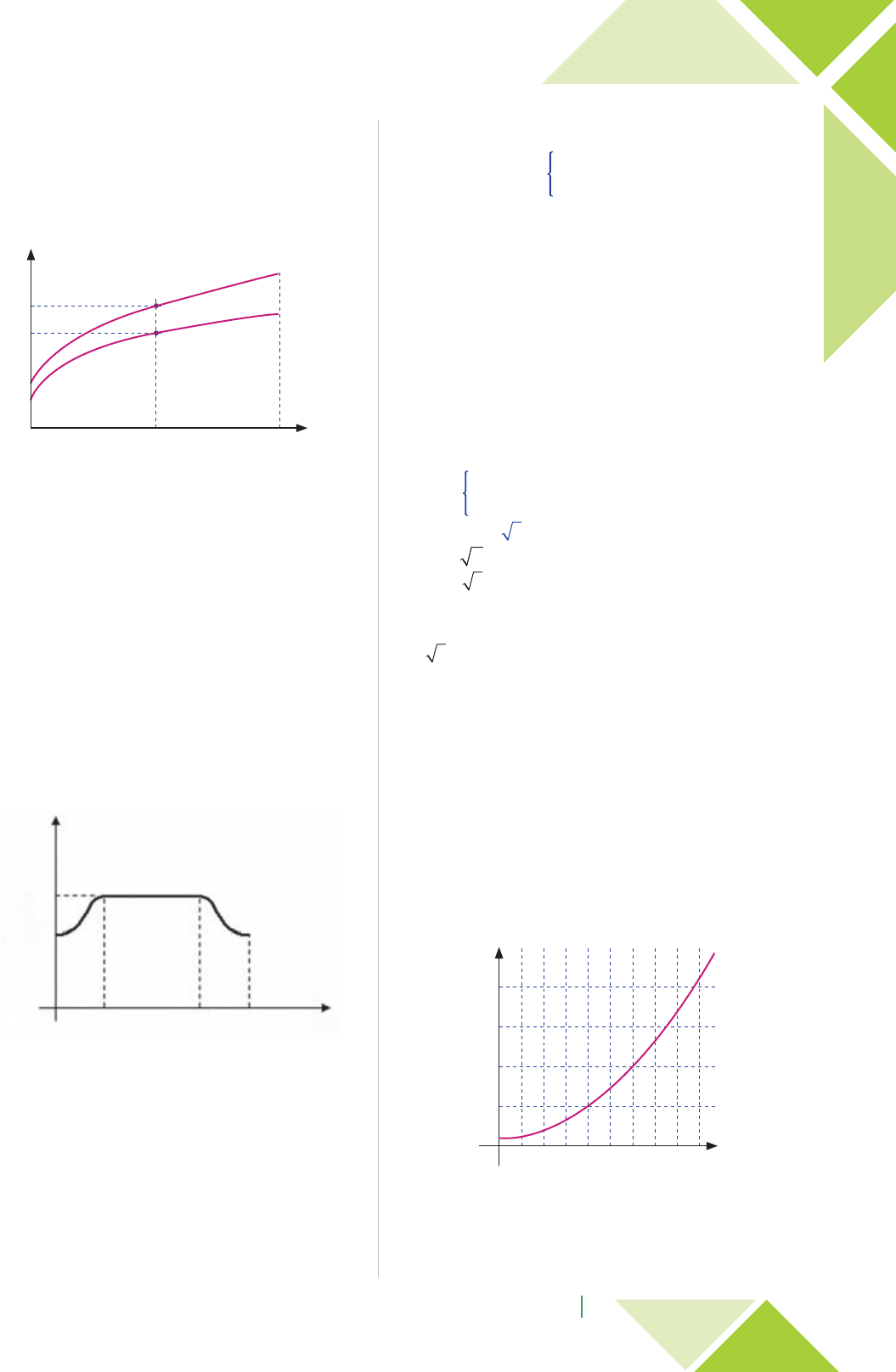
05.09. (UFRGS) – As estimativas para o uso da água pelo
homem, nos anos 1900 e 2000, foram, respectivamente, de
600 km3 e 4.000 k m3 por ano. Em 2025, a expectativa é que
sejam usados 6.000 km3 por ano de água na Terra.
O gráfico abaixo representa o uso da água em k m3 por ano
de 1900 a 2025.
ano
202520001950 197519251900
7000
6000
5000
4000
3000
2000
1000
0
Uso da água (km3 por ano)
Com base nos dados do gráfico, é correto afirmar que,
a) de 1900 a 1925, o uso de água aumentou em 100%.
b) de 1900 a 2000, o uso da água aumentou em mais de
600%.
c) de 2000 a 2025, mantida a expec tativa de uso da água, o
aumento será de 66,6%.
d) de 1900 a 2025, mantida a expectativa de uso da água, o
aumento será de 900%.
e) de 1900 a 2025, mantida a expectativa de uso da água, o
aumento será de 1000%.
Aula 05
7
Matemática 2A
05.10. (UNESP – SP) – A figura representa a evolução da
massa corpórea esperada de bebês ao longo do tempo. A
massa do bebê deve estar na região entre as curvas para que
se considere que ele esteja se desenvolvendo bem. Qual a
menor massa corpórea esperada para um bebê que esteja
se desenvolvendo bem, com idade de 12 meses?
0 2412
2,8
12,2
8,8
4,3
massa (kg)
idade (meses)
a) 15 kg
b) 12,2 kg
c) 8,8 kg
d) 4,3 kg
e) 2,8 kg
05.11. (UERJ ) – O gráfico abaixo representa o consumo
de oxigênio de uma pessoa que se exercita, em condições
aeróbicas, numa bicicleta ergométrica. Considere que o
organismo libera, em média, 4,8 kcal para cada litro de
oxigênio absorvido.
Consumo de O2 (L/min)
0 5 15 20 (mim)
1,4
1,0
A energia liberada no período entre 5 e 15 minutos, em
kcal, é:
a) 48,0
b) 52,4
c) 67,2
d) 93,6
05.12. Considere a função f : IN → Z definida pelo sistema
a seguir:
ƒ(x) = 2, se x é
par
3, se x é
ímpar
O conjunto imagem dessa função é:
a) Z
b) { 0,2,4,6,8,...}
c) { 1,3,5,7,9,...}
d) { 2,3 }
e) {–2, –1, 0 ,1, 2}
05.13. (UFSM – RS) – Considere a função f : IR → IR definida
por
ƒ(x)
= 2x, se x ∈ Q
x2 – 1, se x ∉ Q
A soma ff f() ( ) ()π+ 21− é :
a) π2 + S2– 2
b) 2π + 22
– 2
c) π2 – 2
d) 2π + 1
e) 22
– π + 1
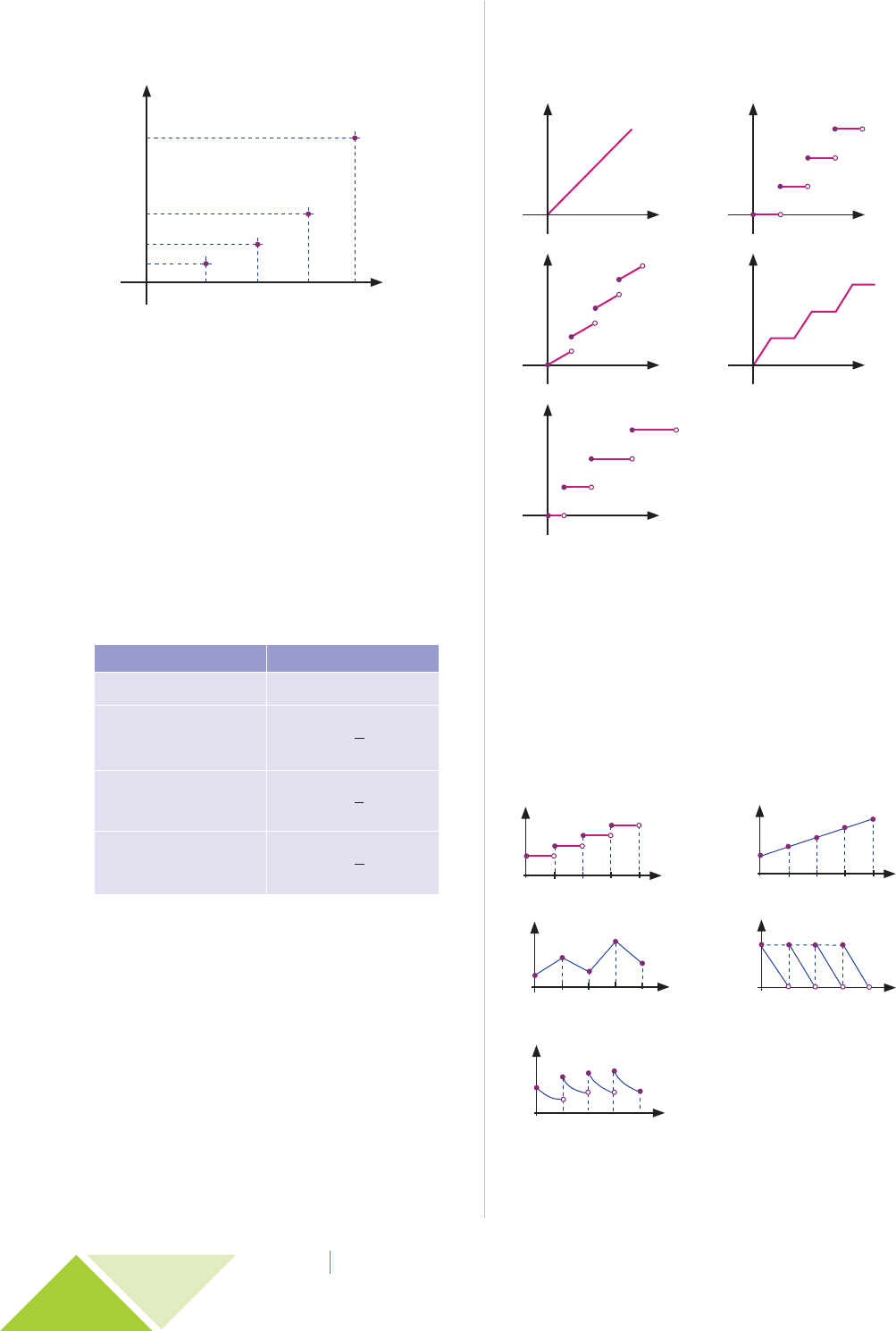
05.14. (FATEC – SP) – Suponha que, em determinada cida-
de, o valor da conta de água residencial em função do seu
consumo seja dado pelo gráfico. Em uma residência, o valor
da conta de água no mês de junho foi de R$ 50,00. Diante
dos gastos, os moradores resolveram economizar e reduzir o
valor da conta à metade. Para tanto, a redução de consumo
deve ser, em metros cúbicos, de
Conta de água (R$)
100
25
50
75
05 45353025201510 40
Consumo (m3)
a) 5. b) 10. c) 15. d) 20. e) 25.
8Extensivo Terceirão
05.15. (UFPA) – No Brasil, uma empresa de comércio para
internet multiplicou suas vendas nos últimos anos, conforme
ilustrado no gráfico abaixo.
1,2
9,6
4,8
2,4
2008 201120102009
Ano
Vendas (milhões de reais)
Em relação às vendas, é correto afirmar que:
a) tiveram um crescimento de 2 milhões de reais de 2008
para 2009.
b) em 2009 cresceram quatro vezes em relação a 2008.
c) triplicaram de 2009 para 2010.
d) em 2010 cresceram 2,4 milhões de reais em relação a
2009.
e) tiveram um crescimento de 4,8 milhões de reais de 2009
para 2011.
05.16. ( VUNESP – SP) – A tabela relaciona as vendas glo-
bais do e -
commerce
realizadas em 2018, e as respectivas
previsões para 2019, 2020 e 2021, cujos valores, em bilhões
de dólares, foram substituídos por x e submúltiplos de x.
ANO VALOR
2018 X
2019 xx1
4
2020 xx1
2
2021 xx3
4
(
O Estado de S. Paulo
– 27.12.2018. Adapatado)
Se as vendas ocorridas em 2018 mais as previsões para os
três anos seguintes totalizam 15,4 bilhões de dólares, então
o valor previsto para as vendas globais do
e - commerce
em
2021 é, em bilhões de dólares, igual a:
a) 5,2
b) 5,0
c) 4,9
d) 4,2
e) 3,5
05.17. (OBMEP) – Lúcia está correndo, sempre no mesmo
sentido, em uma pista circular. Qual dos gráficos melhor
descreve o número m de voltas completas que ela dá em
função da distância x que ela corre?
a)
x
m
c)
x
m
b)
x
m
d)
x
m
e)
x
m
05.18. (UNIFESP – SP) – Uma forma experimental de insuli-
na está sendo injetada a cada 6 horas em um paciente com
diabetes. O organismo usa ou elimina a cada 6 horas 50% da
droga presente no corpo. O gráfico que melhor representa a
quantidade Y da droga no organismo como função do tempo
em um período de 24 horas, é:
a)
Y
0 6 12 18 24 t
b)
Y
0 6 12 18 24 t
c)
Y
0612 18 24 t
d)
Y
0 6 12 18 24 t
e)
Y
0 6 12 18 24 t
Aula 05
9
Matemática 2A
05.19. (UFMG) – O preço de um determinado produto foi
reajustado da seguinte forma: de 15 de março a 15 de abril
sofreu um aumento de 30%; de 15 de março a 15 de maio,
56%; de 15 de março a 15 de junho, 48,2% e de 15 de março
a 15 de julho, 90%. No gráfico a seguir está representada
essa situação.
90%
56%
48,2%
30%
15/03 15/04 15/05 15/0615/07
O índice de reajuste do mês é a variação percentual do preço
entre o dia 15 do mês anterior e o dia 15 do mês em questão.
a) Se o preço do produto em 15/04 era R$26,00, o preço em
15/03 e em 15/05
b) Calcule o percentual de redução do preço de 15/05 a
15/06.
05.20. ( VUNESP – SP ) – Na tabela a seguir, são apresentados
dados dos números de matrículas no ensino pré - escolar,
fundamental e médio da cidade de Itapevi:
Ensino/Ano 2017 2015 2012 2009 2007
Pré -escolar 6 807 5 852 6 031 4 160 6 272
Fundamental 33 583 33 440 35 862 38 702 35 652
Médio 10 331 10 407 11 078 9 905 8 565
(Fonte: IBGE)
Em cada ano, pode -se obter o número total de matrículas
registradas na cidade considerando-se os três níveis de
ensino apresentados na tabela. O gráfico que melhor re -
presenta a variação nesse total de matrículas ao longo dos
anos considerados é:
a)
2007 2009 2012 2015 2017
b)
2007 2009 2012 2015 2017
c)
2007 2009 2012 2015 2017
d)
2007 2009 2012 2015 2017
e)
2007 2009 2012 2015 2017
10 Extensivo Terceirão
05.01. c
05.02. F , V , F , V , F , V
05.03. e
05.04. c
05.05. a) A
b) B
c) Im(f ) = { –8, –6, –4, –2, 0 }
d) x = - 1
05.06. F , V , F , F , V
05.07. c
05.08. e
05.09. d
05.10. c
05.11. a
05.12. d
05.13. c
05.14. b
05.15. d
05.16. c
05.17. b
05.18. e
05.19. a) R$20,00 e R$31,20
b) 5%
Observe o gráfico.
90%
56%
48,2%
30%
15/03 15/04 15/05 15/06 15/07
Gabarito
a) O preço do produto em 15/04 era R$26,00 e queremos o preço
em 15/03 e em 15/05, portanto:
15/04 -------------R$ 26,00 --------------------- 130%
15/03 ------------------ x ---------------------------100%
x = R$ 20,00
15/03 ------------------ R$ 20,00 ---------------------------100%
15/05 ------------------------y------------------------------- 156%
y = R$31,20
Logo, em 15/03 o preço era R$20,00 e em 15/05 o preço era
R$31,20.
b) 15/03 ------------------ R$ 20,00 ---------------------------100%
15/06 ------------------------z------------------------------- 148,2%
z = R$29,64
15/05 ---------------------- R$31,20----------------------------- 100 %
15/06 ---------------------- R$29,64----------------------------- w %
w = 95%
Logo, o percentual de redução do preço de 15/05 a 15/06 foi de
5%.
05.20. a
ENSINO/ANO 2017 2015 2012 2009 2007
Pré -escolar 6 807 5 852 6 031 4 160 6 272
Fundamental 33 583 33 440 35 882 38 702 35 652
Médio 10 331 10 407 11 078 9 905 8 565
Total 50 721 49 699 52 971 52 767 50 487
aumentou diminuiu aumentou aumentou
Das alternativas o gráfico que mais se assemelha a essa situação
da tabela é alternativa
a
Prévia do material em texto
Funções: gráfico, domínio,
imagem, contradomínio e
crescimento
05
Aula
2A
Matemática
1
No plano cartesiano, a cada ponto associamos um
par ordenado e, reciprocamente, a cada par ordenado
existe em correspondência um ponto. Essa associação
nos permite representar o comportamento gráfico de
uma função.
y
f
P
2
1 x
No gráfico acima, o ponto P(1; 2) pertencente à curva
é tal que f(1) = 2, isto é, 2 é a imagem de 1 por meio da
função f. A análise gráfica de uma função permite-nos
compreender como as grandezas que definem a função
estão relacionadas.
Gráfico de uma função
Como numa função y = f(x) associamos valores
de duas grandezas, podemos utilizar essa ideia para
“visualizarmos” o comportamento de uma função.
Assim, ficará mais evidente a relação existente entre as
variáveis envolvidas na função. A construção do gráfico
de uma função a partir de sua lei de formação segue as
seguintes etapas:
• Atribuem-se valores do domínio da função à
variável x;
• Obtêm-se valores para a variável dependente y;
• A cada par ordenado (x; y) localiza-se um ponto no
plano cartesiano;
• Ligam-se convenientemente os pontos para obter-
-se o gráfico.
Exemplo:
Vamos construir, no plano cartesiano, o gráfico
da função que relaciona x e y, conforme a sentença
y = f(x) = 2x, sendo x e y números reais.
Atribuem-se valores para x, calculando
os correspondentes valores para y.
x = – 3 → y = f(– 3) = 2 ∙ (– 3) = – 6 (– 3; – 6)
x = – 2 → y = f(– 2) = 2 ∙ (– 2) = – 4 (– 2; – 4)
x = – 1 → y = f(– 1) = 2 ∙ (– 1) = – 2 (– 1; – 2)
x = 0 → y = f(0) = 2 ∙ 0 = 0 (0; 0)
x = 1 → y = f(1) = 2 ∙ 1 = 2 (1; 2)
x = 2 → y = f(2) = 2 ∙ 2 = 4 (2; 4)
x = 3 → y = f(3) = 2 ∙ 3 = 6 (3; 6)
x = 4 → y = f(4) = 2 ∙ 4 = 8 (4; 8)
2 Extensivo Terceirão
Localizamos os pontos correspondentes a esses
pares ordenados no plano cartesiano, obtendo
assim apenas alguns pontos.
Os pontos devem ser ligados convenientemente confor-
me o domínio da função. Se o domínio é o conjunto dos
números reais, ligamos os pontos de forma contínua.
y
0
2
x
8
7
6
5
4
3
1
–1–3 –2 1 2 43
–1
–3
–2
–6
–5
–4
y
x
y = 2x
• Domínio é o conjunto formado por todos os valores da variável independente x;
Representamos por D(f)
• Imagem é o conjunto formado por todos os valores da variável dependente y, tal que y = f(x);
Representamos por Im(f)
• Contradomínio é o conjunto B correspondente à f: A B
Observações:
1. Quando escrevemos uma função f: A B, o conjunto A é denominado domínio da função e é representado por
D(f ). Já o conjunto B é o contradomínio e representamos por CD(f ).
2. Caso não sejam indicados, convencionamos que o domínio e o contradomínio de uma função é o conjunto dos
números reais .
Conforme diagrama ao lado, temos:
• Domínio:
D(f) = A = {– 1; 0; 1; 2}
• Imagem:
Im(f ) = {7; 8; 9; 10}
• Contradomínio:
CD(f) = B = {5; 6; 7; 8; 9; 10; 11}
A B
– 1
0
1
2
5
6
7
8
9
10
11
f : A B
Aula 05
3Matemática 2A
Crescimento de uma função
No estudo de algumas funções, observamos que, sempre que aumentamos o valor da variável independente x, o
valor da variável dependente y também aumenta. Essas funções são ditas crescentes. Também existem funções que,
sempre quando aumentamos o valor da variável indepente x, o valor da variável dependente y diminui. Tais funções
são denominadas funções decrescentes.
01. (UFPR) – Um estudo feito com certo tipo de bactérias detectou que, no decorrer de uma infecção, a quantidade
dessas bactérias no corpo de um paciente varia aproximadamente segundo uma função q(t) que fornece o número
de bactérias em milhares por mm3 de sangue no instante t. O gráfico da função q(t) encontra-se esboçado abaixo.
O tempo é medido em horas, e o instante t = 0 corresponde ao momento do contágio.
00 4824 t
1
4
3
2
q(t)
Com base nessas informações, considere as seguintes afir-
mações:
I. A função q(t) é crescente no intervalo [0; 48]
II. A quantidade máxima de bactérias é atingida 24 horas
após o contágio, aproximadamente.
III. 60 horas após o contágio, a quantidade de bactérias está
abaixo de 1500 por mm3.
Situações para resolver
• Gráfico de uma função decrescente
Uma função f é dita decrescente quando para todo
x1 < x2, pertencentes ao domínio da função, tem-se
f(x1) > f(x2).
y
f(x1)
f(x2)
xx1 x2
• Gráfico de uma função crescente
Uma função f é dita crescente quando para todo
x1 < x2, pertencentes ao domínio da função, tem-se
f(x1) < f(x2).
y
f(x1)
f(x2)
xx1 x2
Assinale a alternativa correta.
a) Somente as afirmativas I e II são verdadeiras.
c) Somente as afirmativas II e III são verdadeiras.
e) Somente a afirmativa III é verdadeira.
b) Somente as afirmativas I e III são verdadeiras.
d) Somente a afirmativa I é verdadeira.
02. (UFSCAR – SP) – Para estimar a área da figura ABDO (sombreada no
desenho), onde a curva AB é parte da representação gráfica da função
f(x) = 2x, João demarcou o retângulo OCBD e, em seguida, usou um
programa de computador que “plota” pontos aleatoriamente no interior
desse retângulo. Sabendo que dos 1000 pontos “plotados” apenas 540
ficaram no interior da figura ABDO, a área estimada dessa figura, em uni-
dades de área, é igual a
a) 4,32 b) 4,26
c) 3,92 d) 3,84
e) 3,52
C B
A
O
x
y
D = 2
4 Extensivo Terceirão
Testes
Assimilação
05.01. O diagrama abaixo representa uma função f de A em B. O domínio, a imagem e f(4) são, respectivamente:
A B
0
1
2
3
4
5
7
9
11
13
15
17
a) {0,1,2,3,4}, {5,7,9,11,13,15,17} e 7 b) {5,7,9,11,13,15,17},{ 0,1,2,3,4,5} e 9
c) {0,1,2,3,4}, {5,7,13,15} e 7 d) {5,7,13,15}, {5,7,9,11,13,15,17} e 15
e) {0,1,2,3,4}, {9,11,17} e 7
Aula 05
5Matemática 2A
O valor da expressão E = f (3) + f (2 ) + f5
1
3
⎛
⎝
⎜
⎞
⎠
⎟ pertence
ao conjunto
a) {x ∈ IR / –2 < x ≤ –1}
b) {x ∈ IR/ –1 < x ≤ 0}
c) {x ∈ IR / 1 < x ≤ 2}
d) {x ∈ IR / 0 < x ≤ 1}
Aperfeiçoamento
05.05. Dados os conjuntos A = {–3, –2, –1, 0, 1} e
B = { –8, –7, –6, –5, –4, –3, –2, –1, 0, 1 ,2} , considere a função
f de A em B, definida por f(x) = 2x – 2. Determine:
a) O domínio de f
b) O contradomínio de f
c) A imagem de f
d) x sendo f(x) = –4
05.02. Coloque V ou F, conforme as afirmações abaixo
sejam verdadeiras ou falsas, respectivamente, em relação
ao gráfico abaixo:
( ) f(–2) = 1
( ) f( 3) = 0
( ) f(1) = 2
( ) f(0) > 1
( ) Dom(f ) = ]-4:4]
( ) Im(f ) = [–3, 3]
05.03. O conjunto imagem da função abaixo, é:
a) [– 4: 4]
b) ]– 4; 4[
c) [– 3; 3]
d) ]– 3; 3[
e) IR
05.04. (CEFET – MG) – Na figura, está representado o gráfico
da função f : R → R, tal que f (x) = y.
y
2
1
1 2
3 4
–1
0
0,5
f
x
6 Extensivo Terceirão
05.06. (UFPE) – O gráfico a seguir fornece o perfil do lucro
de uma empresa agrícola ao longo do tempo, sendo o ano
zero, o ano de sua fundação. Analisando o gráfico, julgue as
afirmativas:
10
LUCRO
15 20 255 ANO
( ) 10 foi o único ano em que ela foi deficitária.
( ) 20 foi o ano de maior lucro.
( ) 25 foi um ano deficitário.
( ) 15 foi um ano de lucro.
( ) 5 foi o ano de maior lucro no período que vai da fun-
dação até o ano 15.
05.07. (CEFET – SC) – A velocidade de um carro é medida
durante 30s. O gráfico a seguir mostra a variação dessa ve-
locidade v (em Km/h) ao longo do tempo t (em s).
60
V (km/h)
5 12 20 25 30 t(s)
Leia atentamente as afirmativas abaixo:
I. O automóvel permaneceu parado nos primeiros 5 se-
gundos analisados.
II. Entre os instantes 12s e 20s a velocidade do automóvel
variou.
III. O carro não se movimentou entre os instantes 12s e 20s.
IV. A velocidade que o carro atingiu no instante 10s voltou
a ser atingida entre os instantes 20s e 25s.
Estão CORRETAS apenas as afirmativas:
a) I, II e IV.
b) II e IV.
c) I e IV.
d) I, III e IV.
e) III e IV.
05.08.(IBMEC – SP) – Na figura está representado o preço
de um console de video game, em função do tempo decor-
rido desde o seu lançamento.
2,75
3,00
2,50
2,25
2,00
1,75
1,50
1,25
1,00
0,75
0,50
0,25
0
0 1512963
t (meses)
p (milhares de reais)
O preço do aparelho será menor do que 50% do valor de
lançamento a partir do
a) 6. o mês. b) 8. o mês. c) 10. o mês.
d) 12. o mês. e) 14. o mês.
05.09. (UFRGS) – As estimativas para o uso da água pelo
homem, nos anos 1900 e 2000, foram, respectivamente, de
600 km3 e 4.000 km3 por ano. Em 2025, a expectativa é que
sejam usados 6.000 km3 por ano de água na Terra.
O gráfico abaixo representa o uso da água em km3 por ano
de 1900 a 2025.
ano
202520001950 197519251900
7000
6000
5000
4000
3000
2000
1000
0
Uso da água (km3 por ano)
Com base nos dados do gráfico, é correto afirmar que,
a) de 1900 a 1925, o uso de água aumentou em 100%.
b) de 1900 a 2000, o uso da água aumentou em mais de
600%.
c) de 2000 a 2025, mantida a expectativa de uso da água, o
aumento será de 66,6%.
d) de 1900 a 2025, mantida a expectativa de uso da água, o
aumento será de 900%.
e) de 1900 a 2025, mantida a expectativa de uso da água, o
aumento será de 1000%.
Aula 05
7Matemática 2A
05.10. (UNESP – SP) – A figura representa a evolução da
massa corpórea esperada de bebês ao longo do tempo. A
massa do bebê deve estar na região entre as curvas para que
se considere que ele esteja se desenvolvendo bem. Qual a
menor massa corpórea esperada para um bebê que esteja
se desenvolvendo bem, com idade de 12 meses?
0 2412
2,8
12,2
8,8
4,3
massa (kg)
idade (meses)
a) 15 kg
b) 12,2 kg
c) 8,8 kg
d) 4,3 kg
e) 2,8 kg
05.11. (UERJ) – O gráfico abaixo representa o consumo
de oxigênio de uma pessoa que se exercita, em condições
aeróbicas, numa bicicleta ergométrica. Considere que o
organismo libera, em média, 4,8 kcal para cada litro de
oxigênio absorvido.
Co
ns
um
o
de
O
2 (
L/
m
in
)
0 5 15 20 (mim)
1,4
1,0
A energia liberada no período entre 5 e 15 minutos, em
kcal, é:
a) 48,0
b) 52,4
c) 67,2
d) 93,6
05.12. Considere a função f: IN → Z definida pelo sistema
a seguir:
ƒ(x) =
2, se x é par
3, se x é ímpar
O conjunto imagem dessa função é:
a) Z
b) { 0,2,4,6,8,...}
c) { 1,3,5,7,9,...}
d) { 2,3 }
e) {–2, –1, 0 ,1, 2}
05.13. (UFSM – RS) – Considere a função f: IR → IR definida
por ƒ(x) =
2x, se x ∈ Q
x2 – 1, se x ∉ Q
A soma f f f( ) ( ) ( )π + 2 1− é :
a) π2 + 2 – 2
b) 2π + 2 2 – 2
c) π2 – 2
d) 2π + 1
e) 2 2 – π + 1
05.14. (FATEC – SP) – Suponha que, em determinada cida-
de, o valor da conta de água residencial em função do seu
consumo seja dado pelo gráfico. Em uma residência, o valor
da conta de água no mês de junho foi de R$ 50,00. Diante
dos gastos, os moradores resolveram economizar e reduzir o
valor da conta à metade. Para tanto, a redução de consumo
deve ser, em metros cúbicos, de
Co
nt
a
de
á
gu
a
(R
$)
100
25
50
75
0 5 45353025201510 40
Consumo (m3)
a) 5. b) 10. c) 15. d) 20. e) 25.
8 Extensivo Terceirão
05.15. (UFPA) – No Brasil, uma empresa de comércio para
internet multiplicou suas vendas nos últimos anos, conforme
ilustrado no gráfico abaixo.
1,2
9,6
4,8
2,4
2008 201120102009
Ano
Vendas (milhões de reais)
Em relação às vendas, é correto afirmar que:
a) tiveram um crescimento de 2 milhões de reais de 2008
para 2009.
b) em 2009 cresceram quatro vezes em relação a 2008.
c) triplicaram de 2009 para 2010.
d) em 2010 cresceram 2,4 milhões de reais em relação a
2009.
e) tiveram um crescimento de 4,8 milhões de reais de 2009
para 2011.
05.16. (VUNESP – SP) – A tabela relaciona as vendas glo-
bais do e-commerce realizadas em 2018, e as respectivas
previsões para 2019, 2020 e 2021, cujos valores, em bilhões
de dólares, foram substituídos por x e submúltiplos de x.
ANO VALOR
2018 X
2019 x x
1
4
2020 x x
1
2
2021 x x
3
4
(O Estado de S. Paulo – 27.12.2018. Adapatado)
Se as vendas ocorridas em 2018 mais as previsões para os
três anos seguintes totalizam 15,4 bilhões de dólares, então
o valor previsto para as vendas globais do e-commerce em
2021 é, em bilhões de dólares, igual a:
a) 5,2
b) 5,0
c) 4,9
d) 4,2
e) 3,5
05.17. (OBMEP) – Lúcia está correndo, sempre no mesmo
sentido, em uma pista circular. Qual dos gráficos melhor
descreve o número m de voltas completas que ela dá em
função da distância x que ela corre?
a)
x
m
c)
x
m
b)
x
m
d)
x
m
e)
x
m
05.18. (UNIFESP – SP) – Uma forma experimental de insuli-
na está sendo injetada a cada 6 horas em um paciente com
diabetes. O organismo usa ou elimina a cada 6 horas 50% da
droga presente no corpo. O gráfico que melhor representa a
quantidade Y da droga no organismo como função do tempo
em um período de 24 horas, é:
a)
Y
0 6 12 18 24 t
b)
Y
0 6 12 18 24 t
c)
Y
0 6 12 18 24 t
d)
Y
0 6 12 18 24 t
e)
Y
0 6 12 18 24 t
Aula 05
9Matemática 2A
05.19. (UFMG) – O preço de um determinado produto foi
reajustado da seguinte forma: de 15 de março a 15 de abril
sofreu um aumento de 30%; de 15 de março a 15 de maio,
56%; de 15 de março a 15 de junho, 48,2% e de 15 de março
a 15 de julho, 90%. No gráfico a seguir está representada
essa situação.
90%
56%
48,2%
30%
15/03 15/0415/05 15/0615/07
O índice de reajuste do mês é a variação percentual do preço
entre o dia 15 do mês anterior e o dia 15 do mês em questão.
a) Se o preço do produto em 15/04 era R$26,00, o preço em
15/03 e em 15/05
b) Calcule o percentual de redução do preço de 15/05 a
15/06.
05.20. (VUNESP – SP ) – Na tabela a seguir, são apresentados
dados dos números de matrículas no ensino pré-escolar,
fundamental e médio da cidade de Itapevi:
Ensino/Ano 2017 2015 2012 2009 2007
Pré-escolar 6 807 5 852 6 031 4 160 6 272
Fundamental 33 583 33 440 35 862 38 702 35 652
Médio 10 331 10 407 11 078 9 905 8 565
(Fonte: IBGE)
Em cada ano, pode-se obter o número total de matrículas
registradas na cidade considerando-se os três níveis de
ensino apresentados na tabela. O gráfico que melhor re-
presenta a variação nesse total de matrículas ao longo dos
anos considerados é:
a)
2007 2009 2012 2015 2017
b)
2007 2009 2012 2015 2017
c)
2007 2009 2012 2015 2017
d)
2007 2009 2012 2015 2017
e)
2007 2009 2012 2015 2017
10 Extensivo Terceirão
05.01. c
05.02. F , V , F , V , F , V
05.03. e
05.04. c
05.05. a) A
b) B
c) Im(f ) = { –8, –6, –4, –2, 0 }
d) x = - 1
05.06. F , V , F , F , V
05.07. c
05.08. e
05.09. d
05.10. c
05.11. a
05.12. d
05.13. c
05.14. b
05.15. d
05.16. c
05.17. b
05.18. e
05.19. a) R$20,00 e R$31,20
b) 5%
Observe o gráfico.
90%
56%
48,2%
30%
15/03 15/04 15/0515/06 15/07
Gabarito
a) O preço do produto em 15/04 era R$26,00 e queremos o preço
em 15/03 e em 15/05, portanto:
15/04 -------------R$ 26,00 --------------------- 130%
15/03 ------------------ x ---------------------------100%
x = R$ 20,00
15/03 ------------------ R$ 20,00 ---------------------------100%
15/05 ------------------------y------------------------------- 156%
y = R$31,20
Logo, em 15/03 o preço era R$20,00 e em 15/05 o preço era
R$31,20.
b) 15/03 ------------------ R$ 20,00 ---------------------------100%
15/06 ------------------------z------------------------------- 148,2%
z = R$29,64
15/05 ---------------------- R$31,20----------------------------- 100 %
15/06 ---------------------- R$29,64----------------------------- w %
w = 95%
Logo, o percentual de redução do preço de 15/05 a 15/06 foi de
5%.
05.20. a
ENSINO/ANO 2017 2015 2012 2009 2007
Pré-escolar 6 807 5 852 6 031 4 160 6 272
Fundamental 33 583 33 440 35 882 38 702 35 652
Médio 10 331 10 407 11 078 9 905 8 565
Total 50 721 49 699 52 971 52 767 50 487
aumentou diminuiu aumentou aumentou
Das alternativas o gráfico que mais se assemelha a essa situação
da tabela é alternativa a
11Matemática 2A
Matemática
2AAula 06
Funções: função afim
Quando duas grandezas são relacionadasde tal ma-
neira que o gráfico correspondente é uma reta, ou uma
semirreta ou mesmo um segmento de reta, a função que
as relaciona é denominada de função afim.
4
3
2
5
Nesta aula, abordaremos o estudo da chamada fun-
ção afim. Aqui é importante observar como poderemos
resolver dois problemas básicos: a partir da lei de forma-
ção da função, construir o gráfico e, reciprocamente, a
partir do gráfico, obter a lei de formação da função.
Função afim
Inicialmente precisamos definir o que é uma função
afim, observar exemplos e também compreender os sig-
nificados dos termos que aparecem na lei de formação
de tal função.
Função afim
Denomina-se função afim toda função real
y = f(x) cuja lei de formação é da forma
y = f(x) = ax + b
sendo a, b .
Exemplos de função afim:
• y f x x
a
b
= = − →
=
= −
⎧
⎨
⎩
( ) 7 10
7
10
• y f x x
a
b
= = − →
= −
=
⎧
⎨
⎩
( ) 4
4
0
• y f x x
a
b
= = − + →
= −
=
⎧
⎨
⎩
( ) 21
1
21
• y f x
a
b
= = →
=
=
⎧
⎨
⎩
( ) 48
0
48
Observações:
1. Numa função afim da forma y = ax + b, o coeficiente
de x (a) representa a taxa de crescimento da função,
isto é:
a
y
x
f x f x
x x
=
Δ
Δ
=
−
−
( ) ( )2 1
2 1
f(x2)
f(x1)
x1 x2
x
y
2. O termo independente de x (b) indica onde o gráfico
da função intersecta o eixo das ordenadas.
(0, b)
Gráfico de uma função afim
A construção do gráfico de uma função afim pode
ser feita atribuindo-se valores à variável independente
x e obtendo-se os correspondentes valores da variável
dependente y. Quando o domínio da função afim é o
12 Extensivo Terceirão
conjunto dos números reais, o seu gráfico, no plano cartesiano, é uma reta. Existem três possibilidades quanto ao
crescimento do gráfico da função afim:
y
x
a > 0 função crescente a < 0 função decrescente
y
x
a = 0 função constante
y
x
01. Numa função afim f(x) = ax + b, tem-se que f(0) = 10 e f(– 2) = 0. Determine a lei de formação dessa função.
• Como conhecemos as imagens de dois valores de x, podemos determinar os valores de a e b:
f(0) = 10
a . 0 + b = 10 → b = 10
f(– 2) = 0
a . (– 2) + 10 = 0 → a = 5
• A lei de formação da função afim é f(x) = 5x + 10
02. Para produzir um objeto, uma firma gasta R$ 1,20 por unidade. Além disso, há uma despesa fixa de R$ 4 000,00,
independente da quantidade produzida. O preço de venda é de R$ 2,00 por unidade. Qual é o número mínimo de
unidades a partir do qual a firma começa a ter lucro?
• Lembrando que lucro é a diferença entre os valores de venda e de custo, podemos inicialmente obter a lei de
formação da função, sendo x a quantidade produzida e vendida:
L = V – C
L = 2,00x – (4 000 + 1,20x)
L = 0,80x – 4 000
• Impomos a condição do lucro ser maior que zero:
L > 0
0,80x – 4 000 > 0
0,80x > 4 000
8x > 40 000 → x > 5 000
• Portanto, a partir da produção de 5 001 unidades haverá lucro.
Situações resolvidas
01. (PUC – SP) – Uma empresa concessionária de telefonia móvel oferece as seguintes opções de contratos:
• A – R$ 60,00 pela assinatura mensal e mais R$ 0,30 por minuto de conversação;
• B – R$ 40,00 pela assinatura mensal e mais R$ 0,80 por minuto de conversação.
Nessas condições, depois de quantos minutos de conversação em um mês, a opção pelo contrato A se torna mais
vantajosa do que a opção por B?
a) 20 b) 25 c) 40 d) 45 e) 60
Situações para resolver
02. (UERJ) – Em uma partida, Vasco e Flamengo levaram ao
Maracanã 90 000 torcedores. Três portões foram abertos às
12 horas e até às 15 horas entrou um número constante de
pessoas por minuto. A partir desse horário, abriram-se mais 3
portões e o fluxo constante de pessoas aumentou. Os pontos
que definem o número de pessoas dentro do estádio em fun-
ção do horário de entrada estão contidos no gráfico ao lado.
Quando o número de torcedores atingiu 45 000, o relógio es-
tava marcando 15 horas e:
a) 20 min
b) 30 min
c) 40 min
d) 50 min
horário
n.o de pessoas
12 1715
90 000
30 000
45 000
Aula 06
13Matemática 2A
Testes
Assimilação
06.01. Sendo todas as funções das afirmativas abaixo defi-
nidas de IR em IR, classifique-as em V ou F, conforme sejam
verdadeiras ou falsas, respectivamente:
( ) A função f(x) = 2x – 2 é crescente e seu gráfico inter-
secta o eixo das abscissas no ponto (1; 0).
( ) A função g(x) = –6x – 12 é decrescente e seu gráfico
intersecta o eixo das ordenadas no ponto (0 ; – 12).
( ) A função h(x) = 7 é constante e Im(h) = { 7 }
( ) O gráfico da função p(x) = x – 4 forma, com os eixos
coordenados um triângulo retângulo cuja área é, em
unidades de área, igual a 16.
( ) O ponto (–6; 10) pertence ao gráfico da função
q(x) = –6x + 10
06.02. A função f que é definida pelo gráfico a seguir, é:
–1
1
3 X
Y
a) f(x) = –x – 3
b) f(x) = –
1
3
x – 1
c) f(x) = –3x –1
d) f(x) = 3x –1
e) f(x) = – 1
3
x – 1
06.03. Assinale a alternativa que indica corretamente taxa
de crescimento dessa função, sabendo-se que os pontos A
e B são, respectivamente (1; –2) e (2; –1).
–1
1
–1
–2
–3
0
0
A
2 3
B
1
a) 1
b) 2
c) 3
d) 4
e) 5
14 Extensivo Terceirão
06.04. Observando o gráfico abaixo da função f: IR → IR
definida por f(x) = ax +b, temos necessariamente:
Y
X
a) a > 0, b <0 e zero da função um valor positivo
b) a < 0, b <0 e zero da função um valor positivo
c) a > 0, b > 0 e zero da função um valor negativo
d) a < 0, b <0 e zero da função um valor positivo
e) a > 0, b <0 e zero da função um valor negativo
Aperfeiçoamento
06.05. (IFSUL – RS) – Numa serigrafia, o preço y de cada
camiseta relaciona-se com a quantidade x de camisetas
encomendadas, através da fórmula y = –0,4x + 60. Se fo-
ram encomendadas 50 camisetas, qual é o custo de cada
camiseta?
a) R$ 40,00
b) R$ 50,00
c) R$ 70,00
d) R$ 80,00
06.06. (EEAR – SP) – A função que corresponde ao gráfico
a seguir é f(x) = ax + b, em que o valor de a é:
Y
X3
6
a) 3
b) 2
c) –2
d) –1
06.07. (PUCPR) – Uma função afim f(x), cuja forma é
f(x) = ax + b, com a e b números reais. Se f(–3) = 3 e
f(3) = –1, os valores de a e b, são respectivamente:
a) 2 e 9
b) 1 e –4
c)
1
3
3
5
e
d) 2 e –7
e)
2
3
1e
06.08. (IFAL) – Os pontos de um plano cartesiano de coor-
denadas (2,2)e (4, –2) pertencem ao gráfico de uma função
definida por f(x) = ax + b. Qual o valor de a + b?
a) 0.
b) 2.
c) 4.
d) 6.
e) 8.
06.09. (PUC – RJ) – Considere a função real da forma
f(x) = ax + b. Sabendo que f(1) = –1 e f(0) = 2, qual é o valor
do produto a · b?
a) 1
b) 6
c) –3
d) –4
e) –6
Aula 06
15Matemática 2A
06.10. (UFPR) – O ângulo de visão de um motorista diminui
conforme aumenta a velocidade de seu veículo. Isso pode re-
presentar riscos para o trânsito e os pedestres, pois o condutor
deixa de prestar atenção a veículos e pessoas fora desse ângulo
conforme aumenta sua velocidade. Suponha que o ângulo de
visão A relaciona-se com a velocidade v através da expressão
A = k v + b, na qual k e b são constantes. Sabendo que o
ângulo de visão a 40 km/h é de 100°, e que a 120 km/h fica
reduzido a apenas 30°, qual o ângulo de visão do motorista
à velocidade de 64 km/h?
a) 86°
b) 83°
c) 79°
d) 75°
e) 72°
Aprofundamento
06.11. (ESPM – SP) – O gráfico abaixo mostra a variação da
temperatura no interior de uma câmara frigorífica desde o
instante em que foi ligada. Considere que essa variação seja
linear nas primeiras 2 horas.
80
tempo (min)
60
40
200
20
60
48
24
temperatura (oC)
0
40
O tempo necessário para que a temperatura atinja –18 °C
é de:
a) 90 min
b) 84 min
c) 78 min
d) 88 min
e) 92 min
06.12. (FATEC – SP) – O Teorema de Stevin relaciona a
pressão atmosférica e a pressão nos líquidos. Para um líquido
homogêneo, em equilíbrio, cuja superfície está sob ação da
pressão atmosférica, a pressão (P) exercida em um ponto
submerso qualquer do líquido em relação à altura da coluna
de líquido (h) é dada por uma função polinomial do 1.º grau.
O gráfico apresenta a variação da pressão (P) em funçãoda
altura da coluna de líquido (h) em um tanque de combustível.
0 10
1,00
h(m)
1,75
P(×105Pa)
Nessas condições, a pressão (P) exercida em um ponto desse
líquido que se encontra a 4 m de profundidade é, em Pa;
a) 1,3 × 100
b) 1,6 × 100
c) 1,3 × 103
d) 1,3 × 105
e) 1,6 × 105
06.13. (FGV – SP) – No final do ano 2012, José Carlos com-
prou um carro 0km. Devido à depreciação, dois anos depois
da compra, o valor do carro era R$ 46 000,00 e, cinco anos
após a compra, ele valia R$ 40 000,00. Admitindo que o valor
do carro decresça linearmente com o tempo, pode-se afirmar
que 8 anos e 3 meses após a compra o seu valor será:
a) R$ 33 000,00
b) R$ 34 000,00
c) R$ 32 500,00
d) R$ 33 500,00
e) R$ 32 000,00
16 Extensivo Terceirão
06.14. (UEG – GO) – A função f(x) que representa o gráfico
a seguir, onde k é uma constante não nula, é dada por:
x
y
k
1 2 3 4 5
a) f x
k
x se x
k se x
( )
,
,
=
≤ ≤
< ≤
⎧
⎨
⎪
⎩⎪
2
0 2
2 5
b) f x
k se x
k se x
( )
,
,
=
≤ ≤
< ≤
⎧
⎨
⎩
0 2
3 2 5
c) f x
k
se x
kx se x
( )
,
,
=
≤ ≤
< ≤
⎧
⎨
⎪
⎩⎪
2
0 2
2 5
d) f x
kx se x
k se x
( )
,
,
=
≤ ≤
< ≤
⎧
⎨
⎩
0 2
2 5
06.15. (FGV – SP) – Uma rede de livrarias estima vender
anualmente 1 500 unidades de determinado livro se o seu
preço unitário de venda for R$50,00. Além disso, a rede esti-
ma que uma queda de R$10,00 no preço de cada exemplar
proporcionará um aumento de vendas de 100 unidades
por ano. Supondo que a relação entre preço e quantidade
vendida anualmente possa ser expressa por uma função
polinomial de 1o. grau, quanto deverá ser cobrado por livro
para maximizar a receita anual?
a) R$ 90,00
b) R$ 100,00
c) R$ 70,00
d) R$ 110,00
e) R$ 80,00
06.16. (IFSC) – Durante a colheita em um pomar de uvas,
o proprietário verificou que às 9 horas haviam sido colhidos
730 kg de uva. Considerando que a quantidade de uvas
colhidas é linear durante o dia e que às 14 horas haviam sido
colhidos 3 650 kg de uva, analise as afirmativas:
I. A equação que permite calcular o número de quilogra-
mas (y) em função do tempo (x) é dada pela expressão
y = 584x – 4 526.
II. Às 18 horas haviam sido colhidos 5 986 kg.
III. A colheita teve início às 8 horas.
Assinale a alternativa CORRETA.
a) Apenas as afirmativas I e II são verdadeiras.
b) Todas as afirmativas são verdadeiras.
c) Apenas as afirmativas I e III são verdadeiras.
d) Apenas as afirmativas II e III são verdadeiras.
e) Todas as afirmativas são falsas.
06.17. (UEG – GO) – No centro de uma cidade, há três
estacionamentos que cobram da seguinte maneira:
Estacionamento A Estacionamento B Estacionamento C
R$ 5,00 pela primeira
hora
R$ 3,00 por cada
hora subsequente
R$ 4,00 por hora
R$ 6,00 pela primei-
ra hora
R$ 2,00 por cada
hora subsequente
Será mais vantajoso, financeiramente, parar
a) no estacionamento A, desde que o automóvel fique
estacionado por quatro horas.
b) no estacionamento B, desde que o automóvel fique
estacionado por três horas.
c) em qualquer um, desde que o automóvel fique estacio-
nado por uma hora.
d) em qualquer um, desde que o automóvel fique estacio-
nado por duas horas.
e) no estacionamento C, desde que o automóvel fique
estacionado por uma hora.
Aula 06
17Matemática 2A
06.18. (UEM – PR) – Duas empresas de telefonia, A e B, têm
os seguintes planos:
• Empresa A: cobra um valor fixo mensal de R$ 19,90 e
mais R$ 0,15 por minuto no valor da ligação.
• Empresa B: cobra um valor fixo mensal de R$ 29,90 e mais
R$ 0,05 por minuto no valor da ligação.
João contratou a empresa A e Maria contratou a empresa B.
Sobre o exposto, assinale o que for correto.
01) Se Maria pagou uma fatura de telefone no valor de
R$ 79,90, então ela realizou mais de 950 minutos em
ligações.
02) Se João realizar, em um mês, 300 minutos em ligações,
então sua conta de telefone no final do mês será de
R$ 44,90.
04) Se João fizer a mesma quantidade de ligações (em
minutos) que Maria, então o valor da conta de telefone
dele é sempre menor que o valor da conta dela.
08) Se Maria fizer duas vezes mais minutos em ligações que
João, então o valor da conta de telefone dela será sempre
maior que o valor da conta de telefone dele.
16) Se uma pessoa utilizar no máximo 90 minutos em liga-
ções por mês, então o plano da empresa A sairá mais
barato que o plano da empresa B.
Desafio
06.19. (EPCAR – MG) – João, ao perceber que seu carro
apresentara um defeito, optou por alugar um veículo para
cumprir seus compromissos de trabalho. A locadora, então,
apresentou-lhe duas propostas:
I. plano A, no qual é cobrado um valor fixo de R$50,00 e
mais R$1,60 por quilômetro rodado;
II. plano B, no qual é cobrado um valor fixo de R$64,00 mais
R$1,20 por quilômetro rodado.
João observou que, para um certo deslocamento que tota-
lizava k quilômetros, era indiferente optar pelo plano A ou
pelo plano B, pois o valor final a ser pago seria o mesmo. É
correto afirmar que k é um número racional entre:
a) 14,5 e 20. b) 20 e 25,5. c) 25,5 e 31. d) 31 e 36,5.
06.20. (UFMG) – A fábula da lebre e da tartaruga, do escritor
grego Esopo, foi recontada utilizando-se o gráfico abaixo para
descrever os deslocamentos dos animais.
240 245 Tempo (min.)5
200
150
100
50
Distância
(em metros)
Suponha que na fábula a lebre e a tartaruga apostam uma
corrida em uma pista de 200 metros de comprimento. As
duas partem do mesmo local no mesmo instante. A tartaruga
anda sempre com velocidade constante. A lebre corre por
5 minutos, para, deita e dorme por certo tempo. Quando
desperta, volta a correr com a mesma velocidade constante
de antes, mas, quando completa o percurso, percebe que
chegou 5 minutos depois da tartaruga. Considerando essas
informações, determine:
a) Após quanto tempo da largada a tartaruga alcançou a
lebre.
b) Por quanto tempo a lebre ficou dormindo.
18 Extensivo Terceirão
Gabarito
06.01. V , V , V , F , F
06.02. d
06.03. a
06.04. a
06.05. d
06.06. c
06.07. e
06.08. c
06.09. c
06.10. c
06.11. b
06.12. d
06.13. a
06.14. d
06.15. b
06.16. a
06.17. d
06.18. 17(01 + 16)
06.19. [k = 35]
O valor pago pelo carro no plano A e representado pela função f(x) = 50 + 1, 60 ∙ x, sendo x a distância percorrida em quilômetros, e o valor pago
pelo carro no plano B e representado pela função g(x) = 64 + 1, 2 ∙ x. Se para k quilômetros, teremos o mesmo valor, então:
f(x) = g(x) → 50 + 1, 60 ∙ x = 64 + 1, 2 ∙ x → k = 35
Logo, k = 35
06.20. a) 1 hora
b) 3 horas e 45 min
a) Equação da posição y da tartaruga:
(0,0) y = ax + b 0 = a 0 + b b = 0
(240, 200) y = ax +
∈ → ⋅ →
∈ b 200 = a 240 + b 200 = a 240 + 0 a = =→ ⋅ → ⋅ →
⎧
⎨
⎪
⎩⎪
200
240
5
6
A equação da posição y da tartaruga: y x= ⋅5
6
Como a equação da posição y da lebre no instante do encontro é y = 50, então
5
6
50⋅ =x , temos
x = 60 min = 1 hora
Portanto, a lebre e a tartaruga se encontrarão 1 hora após o início da corrida.
b) Se a lebre voltou a correr com a mesma velocidade constante de antes, então a taxa de crescimento da função relativa a lebre antes e depois de
dormir por um tempo, são iguais.
1º trecho de corrida da lebre:
(0,0) y = cx + d 0 = c 0 + d d = 0
(5, 50) y = cx +
∈ → ⋅ →
∈ dd 50 = c 5 + d 50 = c 5 + 0 c = 10→ ⋅ → ⋅ →
⎧
⎨
⎩
1º trecho de corrida da lebre :
(p, 50) y = mx +n
(240,200) y = mx + n
∈
∈
⎧
⎨
⎩
50 = c p + d
⋅
⋅= +
⎧
⎨
⎩200 240c d
c=
⎧
⎨
⎩
150
240−p
Igualando os valores dos termos independentes, temos:
150
240
10 230 5 225
−
−
p
= → =
Portanto, a lebre ficou dormindo 225min = 3 horas e 45 min.
19Matemática 2A
Matemática
2AAula 07
Funções: estudo do sinal de uma
função afim e inequações
Quando o domínio de uma função afim – função da forma f(x) = ax + b – é o conjunto dos números reais, o seu
gráfico, no plano cartesiano, é uma reta. Quanto ao crescimento dessa função, temos as seguintes possibilidades:
a > 0 função crescente a = 0 função constante a < 0 função decrescente
Utilizaremos essas ideias para analisaro sinal de uma função afim e proceder à resolução de inequações que
envolvam sentenças do 1o. grau na incógnita x.
Estudo do sinal de uma função afim
Estudar o sinal de uma função é determinar para que valores da variável x a variável y é positiva, nula ou negativa.
Observe, como exemplos, os gráficos das seguintes funções e as interpretações dos sinais correspondentes:
Sinal da função, conforme o gráfico acima:
• Para x > 1, temos y < 0
• Para x = 1, temos y = 0
• Para x < 1, temos y > 0
y
x
1
y
x
–2
Sinal da função, conforme o gráfico acima:
• Para x > –2, temos y > 0
• Para x = –2, temos y = 0
• Para x < –2, temos y < 0
Embora tenhamos aqui observado apenas o estudo do sinal de funções afins, essa mesma análise pode ser feita
para uma função qualquer por meio do seu gráfico no plano cartesiano. Uma das aplicações desse estudo está na
resolução de inequações do 1º. grau e também de inequações que envolvem o produto ou o quociente de sentenças
do 1o. grau na incógnita x, como exemplificaremos a seguir.
01. Estude o sinal da função afim definida, no conjunto dos números reais, por f x x( ) .= −2 10
02. A inequação a seguir envolve o produto de duas sentenças do 1o. grau na incógnita x. Utilize o estudo do sinal de
uma função afim para resolver essa equação.
( ) ( )2 8 7 0x x− ⋅ − + ≥
03. A inequação 9 3
2 10
0
−
+
≤x
x
é do tipo quociente. Resolva-a, utilizando o estudo de sinal da função afim.
Situações para resolver
20 Extensivo Terceirão
Observação:
As questões e testes desta aula abordam não apenas o estudo do sinal de uma função afim, mas também a
resolução de inequações do 1°. grau e situações diversas relacionadas à função afim.
04. (UFSC) – Dois líquidos diferentes encontram-se em recipientes idênticos e têm taxas de evaporação constantes.
O líquido I encontra-se inicialmente num nível de 100 mm e evapora-se completamente no quadragésimo dia. O
líquido II, inicialmente com nível de 80 mm, evapora-se completamente no quadragésimo oitavo dia. Determinar,
antes da evaporação completa de ambos, ao final de qual dia os líquidos terão o mesmo nível (em mm) nesses
mesmos recipientes.
Aula 07
21Matemática 2A
Testes
Assimilação
07.01. Sobre o gráfico da função afim representado no plano
cartesiano a seguir, classifique-as em V ou F, conforme sejam
verdadeiras ou falsas, respectivamente:
1 2 3 4–4 –3 –2 –1
–1
–2
–3
–4
0
1
2
3
4
( ) f(2) > 0
( ) f(–3) < 0
( ) se x < 0 então f(x) < 0
( ) se x > 0 então f(x) < 0
( ) se x = 0 então f(x) = 0
07.02. Uma função f: IR → IR definida por f(x) = ax +b é
representada no plano cartesiano por uma reta. Assinale o
que for correto:
01) se a > 0 então a reta é crescente.
02) se a > 0 e b > 0 então o zero da função é negativo.
04) se b = 0 a reta é constante.
08) se a > 0 e o zero da função for positivo então b < 0
16) se a = 0 a reta passa pela origem.
07.03. Sobre o gráfico da função afim representado no plano
cartesiano a seguir, classifique-as em V ou F, conforme sejam
verdadeiras ou falsas, respectivamente :
0 5 x
3
y
( ) f(7) > 0
( ) f(–1) < 0
( ) se x < 5 então f(x) < 0
( ) se x > 5 então f(x) < 0
( ) se x = 5 então f(x) = 0
07.04. (UNICAMP – SP) – O gráfico da função y = mx + n
passa pelos pontos A(1,3) e B(2,8). Pode-se afirmar que:
a) A única raiz da função é 4.
b) f(3)= 10
c) f(4)=12
d) f(x) < 0 se, somente se x < 3
e) f(x) > 0 se, somente se x > 2/5
22 Extensivo Terceirão
Aperfeiçoamento
07.05. (UCPEL – RS) – Considerando uma reta r que passa
pelos pontos A(4,6) e B(1,2), pode-se afirmar que:
a) a reta r é crescente.
b) os pontos P(1,2) e Q(−2,3) pertencem à reta r.
c) a reta r passa pela origem do sistema cartesiano ortogonal
e pelo ponto P(1,2).
d) a reta r intercepta o eixo das ordenadas no ponto (0,4).
e) a reta r é paralela ao eixo das abscissas.
07.06. (EPCAR – MG) – Para fazer uma instalação elétrica em
sua residência, Otávio contatou dois eletricistas.
O Sr. Luiz, que cobra uma parte fixa pelo orçamento mais
uma parte que depende da quantidade de metros de fio
requerida pelo serviço. O valor total do seu serviço está
descrito no seguinte gráfico:
100
80
0 15 25
preço (R$)
quantidade
de f io (metros)
Já o Sr. José cobra, apenas, R$ 4,50 por metro de fio utilizado
e não cobra a parte fixa pelo orçamento.
Com relação às informações acima, é correto afirmar que
a) o valor da parte fixa cobrado pelo Sr. Luiz é maior do que
R$ 60,00.
b) o Sr. Luiz cobra mais de R$ 2,50 por metro de fio instalado.
c) sempre será mais vantajoso contratar o serviço do Sr. José.
d) se forem gastos 20 m de fio, não haverá diferença de valor
total cobrado entre os eletricistas.
07.07. (ESPM – SP) – A função f(x) + ax + b é estritamente
decrescente. Sabe-se que f(a) = 2b e f(b) = 2a. O valor de
f(3), é:
a) 2 b) 4 c) –2 d) 0 e) –1
07.08. (UNICESUMAR – PR) – Seja f uma função de em ,
sendo o conjunto dos números reais, definida por
f(x) = 2x – 13, os valores de x pertencentes ao domínio dessa
função e que produzem imagens maiores que 7 são tais que:
a) x < 10
b) 0 < x < 5
c) x ≤ 10
d) 5 ≤ x ≤ 9
e) x > 10
07.09. (UNICAMP – SP) – O gráfico abaixo exibe o lucro
líquido (em milhares de reais) de três pequenas empresas
A, B e C, nos anos de 2013 e 2014.
Lucro líquido (milhares de reais)
600
20142013
Ano
500
400
300
200
100
A
B
C
Com relação ao lucro líquido, podemos afirmar que:
a) A teve um crescimento maior do que C.
b) C teve um crescimento maior do que B.
c) B teve um crescimento igual a A.
d) C teve um crescimento menor do que B.
Aula 07
23Matemática 2A
07.10. (CEFET – SC) – O volume de água em um reservatório
aumenta em função do tempo, de acordo com o gráfico
abaixo:
1
V(m3)
3 t(h)
Para encher este reservatório de água com 2500 litros, uma
torneira é aberta. Qual o tempo necessário para que o reser-
vatório fique completamente cheio?
a) 7 h
d) 7 h 30 min
b) 6 h 50 min
e) 7 h 50 min
c) 6 h 30 min
Aprofundamento
07.11. O produto das soluções inteiras e positivas da ine-
quação (x – 5) ∙ (9 – x) > 0, é:
a) 21 b) 65 c) 177 d) 336 e) 489
07.12. (FGV – SP) – O número de soluções inteiras da ine-
quação 2 6
14 2
0
x
x
+ ≥
−
, é:
a) 8
b) 9
c) 10
d) 11
e) Infinito
07.13. (CEFET – MG) – O número de soluções inteiras per-
tencentes ao conjunto solução da inequação
(3x ) (x )− +9
2
6
3
0⋅ < , é:
a) 4. b) 6. c) 8. d) 10.
07.14. (UEPG – PR) – Miguel e Marlon disputam cem par-
tidas de xadrez. Cada vez que Miguel ganha uma partida,
recebe R$ 4,00 de Marlon e cada vez que Marlon vence uma
partida, recebe R$ 8,00 de Miguel. A partir do que foi exposto,
assinale o que for correto.
01) Se Miguel vencer metade das partidas, terá um prejuízo
de R$ 200,00.
02) Miguel tem lucro, se vencer pelo menos 67 partidas.
04) Marlon tem lucro, se vencer no mínimo 34 partidas.
08) Se Marlon vencer vinte das partidas, terá um prejuízo
exatamente igual ao valor que recebeu.
07.15. (UNIFOR – CE) – A resistência elétrica R, em ohms,
para um fio de metal puro, está relacionada com a sua tem-
peratura T em °C, pela expressão:
R = R0(1 + kT)
na qual R0 e k são constantes positivas. Em teoria, a resistência
R de um fio cai para zero quando a temperatura atinge o zero
absoluto (–273 °C). O valor de k é de:
a)
1
273
c)
R 0
273
e)
1
273
0R
b)
1
273
d)
R 0
273
24 Extensivo Terceirão
07.16. (CEFET – MG) – O número de soluções inteiras da
inequação x x x− < − < +1 3 5 2 1 é
a) 4 b) 3 c) 2 d) 1
07.17. (IFSP) – A capacidade de um reservatório de água
é maior que 250 litros e menor que 300 litros. O número
x de litros que há nesse reservatório satisfaz à inequação
x
2
1 127+ < .
Assinale a alternativa que apresenta quantos litros de água
há nesse reservatório.
a) 250 litros.
b) 251 litros
c) 252 litros.
d) 253 litros.
e) 255 litros.
07.18. (IFSP) – Um espião de guerra enviou ao seu comando
a seguinte mensagem:
5n + 25 > 5500
–8n + 3501> 210 – 5n
O comando sabia que a letra n representava o número de
foguetes do inimigo. Fazendo os cálculos, é correto afirmar
que o total de foguetes que o comando descobriu foi de
a) 3.000 foguetes.
b) 2.192 foguetes.
c) 1.097 foguetes.
d) 1.096 foguetes.
e) 195 foguetes.
07.19. (CEFET – RJ) – Chamamos força do conjunto solu-
ção de um sistema de inequações resolvido no conjunto
dos números inteiros a soma de todos os elementos desse
conjunto solução.
No sistema
2 2 5 13
2 3
1
( )x x
x x
+ ≥ +
− > −
⎧
⎨
⎪
⎩⎪
se x é um número do conjun-
to dos inteiros que torna verdadeiras as inequações, a força
do conjunto solução desse sistema será igual a:
a) –12 b) –9 c) –6 d) –3
07.20. (UFPR) – A figura abaixo representa o quadrilátero do
plano cartesiano delimitado pelo eixo das abscissas e pelo
gráfico da função
f x
x se x
x
se x
x se x
( )
,
( )
=
+ − ≤ ≤
+
≤ ≤
⋅ − ≤ ≤
⎧
⎨
⎪⎪
⎩
⎪
⎪
2 4 2 1
2 52
9
1 10
2 14 10 14
–2 1 10 14
Qual é a área desse quadrilátero?
a) 75
b) 88
c) 95
d) 100
e) 128
Aula 07
25Matemática 2A
Gabarito
07.01. V, V, V, F, V
07.02. F, F, F, V, V
07.03. 11 (01 + 02 + 08)
07.04. e
07.05. a
07.06. d
07.07. c
07.08. e
07.09. b
07.10. d
07.11. d
07.12. c
07.13. c
07.14. 15 (01 + 02 + 04 + 08)
07.15. a
07.16. b
07.17. b
07.18. d
07.19. a
Resolvendo o sistema de inequações, obtemos:
2 2 5 13 2 4 5 13 3 9 1
2 3
1 3 2 6 6
( )x x x x x x
x x
x x x
+ ≥ + ⇒ + ≥ + ⇒− ≥ ⇒ ≤ −
− > − ⇒ − > − ⇒ > −
⎧
⎨
⎪⎪
⎩⎪
Logo, a solução do sistema será dada por todos os números reais
tais que –6 < x ≤ –3 e a força deste conjunto solução será dada por:
(–5) + (–4) + (–3) = –12.
07.20. b
Sendo a função f x
x se x
x
se x
x se x
( )
,
( )
=
+ − ≤ ≤
+
≤ ≤
⋅ − ≤ ≤
⎧
⎨
⎪⎪
⎩
⎪
⎪
2 4 2 1
2 52
9
1 10
2 14 10 14
, temos que:
Se x = 1 temos f(1) = 6 e se x = 10 temos f(10) = 8. Observe o
gráfico.
–2 1 10 14
8
6
Esse quadrilátero pode ser subdividido em três triângulos retângu-
los e um retângulo como no gráfico
–2 1 10 14
8
6
A
B
C
DFE
Considere:
A → área do quadrilátero ABCD
A1 → área do TRIÂNGULO ABE
A2 → área do TRIÂNGULO CDF
A3 → área do TRIÂNGULO BCG
A4 → área do Retângulo EFGB
A = A + A + A + A = + + + 9 6 = 881 2 3 4
3 6
2
4 8
2
9 2
2
Logo, a área do quadrilátero é 88 unidades de área.
26 Extensivo Terceirão
Matemática
2AAula 08
Funções: função quadrática
©
Sh
ut
te
rs
to
ck
/E
SB
P
ro
fe
ss
io
na
l
A imagem é da ponte Juscelino Kubitschek, em Brasília. Nela, é possível perceber uma estrutura em arcos de
parábolas. Parábola é uma curva que, no plano cartesiano, corresponde ao gráfico de uma função quadrática, tam-
bém conhecida como função polinomial do 2° grau. Nesta aula, observaremos como são essas curvas e também a
importância delas em situações diversas.
Função quadrática
No estudo de uma função real qualquer, é importante conhecermos a lei de formação e também o com-
portamento do gráfico correspondente. No caso da função quadrática, esse estudo inicia-se por meio de sua
definição:
Uma função f: � → � é denominada função quadrática, na variável independente x, quando sua lei de for-
mação é da forma
y = f(x) = ax2 + bx + c
sendo a, b, c ∈ � e a ≠ 0.
Assim, são exemplos de funções quadráticas:
• y = f(x) = – 3x2 + 10x – 7 →
a = – 3
b = 10
c = – 7
• y = f(x) = 2x2 + x – 17 →
a = 2
b = 1
c = – 17
Gráfico de uma função quadrática
No plano cartesiano, o gráfico de uma função real quadrática y = f(x) é uma curva denominada parábola. A constru-
ção de tal gráfico pode ser feita atribuindo-se valores à variável independente x e obtendo-se valores correspondentes
para a variável dependente y. Ligando-se esses pontos “convenientemente”, obtemos o gráfico.
Aula 08
27Matemática 2A
A seguir, observe dois exemplos.
Exemplo 1:
O gráfico a seguir é da função quadrática real definida por y = f(x) = x2 – 4
• As coordenadas dos sete pontos indicados no gráfico foram obtidas da seguinte forma:
x = – 3 ⇒ y = f(– 3) = (– 3)2 – 4 = 5
x = – 2 ⇒ y = f(– 2) = (– 2)2 – 4 = 0
x = – 1 ⇒ y = f(– 1) = (– 1)2 – 4 = – 3
x = 0 ⇒ y = f(0) = 02 – 4 = – 4
x = 1 ⇒ y = f(1) = 12 – 4 = – 3
x = 2 ⇒ y = f(2) = 22 – 4 = 0
x = 3 ⇒ y = f(3) = 32 – 4 = 5
Exemplo 2:
O gráfico a seguir é da função quadrática real definida por y = f(x) = – x2 + 4x
• As coordenadas dos sete pontos indicados no gráfico foram obtidas da seguinte forma:
y = f(– 1) = –(– 1)2 + 4(– 1) = – 5
y = f(0) = 02 + 4 ∙ 0 = 0
y = f(1) = – 12 + 4 ∙ 1 = 3
y = f(2) = – 22 + 4 ∙ 2 = 4
y = f(3) = – 32 + 4 ∙ 3 = 3
y = f(4) = – 42 + 4 ∙ 4 = 0
y = f(5) = – 52 + 4 ∙ 5 = – 5
Embora tenhamos apresentado até aqui apenas dois exemplos, de modo geral podemos dizer que existem duas
possibilidades quanto à concavidade da parábola. Essas possibilidades não precisam ser verificadas atribuindo-se
valores para x. Basta observar o sinal do coeficiente do termo em x2, isto é:
Na função f: � → � definida por y = f(x) = ax2 + bx + c, sendo a, b, c ∈ � e a ≠ 0, temos, quanto ao gráfico:
a > 0 → parábola com a concavidade voltada para cima;
a < 0 → parábola com a concavidade voltada para baixo.
Zeros da função quadrática
As abscissas dos pontos do plano cartesiano em que a parábola intersecta o eixo das abscissas são conhecidas
como zeros da função quadrática correspondente, pois nesses pontos a função se anula. No quadro a seguir, temos
as seis possibilidades quanto à concavidade da parábola e aos zeros da função quadrática. Observe que Δ = b2 – 4ac.
y
x
y
x
28 Extensivo Terceirão
Δ > 0 Δ = 0 Δ < 0
a > 0
x1 x2
x1 = x2
∃ x ∈ �/y = 0
a < 0 x1 x2
x1 = x2
∃ x ∈ �/y = 0
Vértice de uma parábola
Toda parábola admite um ponto extremo. Tal ponto é denominado vértice da parábola. Como toda parábola
admite um eixo de simetria (eixo vertical, no caso de função quadrática), o vértice corresponde ao ponto em que esse
eixo intersecta a parábola, conforme pode ser observado a seguir:
y
x
xV
yV
Eixo de
simetria
y
x
Eixo de
simetria
xV
yV
Demonstra-se que as coordenadas desse ponto podem ser determinadas a partir dos valores dos coeficientes a, b
e c da função quadrática correspondente:
Na função quadrática f: � → � definida por y = f(x) = ax2 + bx + c, as coordenadas do vértice V(xV; yV) da pará-
bola são obtidas pelas relações:
xV = –
b
2a
yV = f(xV) = – 4a
Aula 08
29Matemática 2A
Tendo as coordenadas do vértice da parábola, podemos obter o ponto extremo da correspondente função quadrá-
tica e também seu conjunto imagem.
Observação:
Além dos problemas envolvendo máximos e mínimos assumidos por uma função quadrática, interessa-nos
também determinar a variação do y, isto é, o conjunto imagem correspondente. Observe que cada intervalo
destacado no eixo das ordenadas representa o conjunto imagem de uma função quadrática:
Im(f )
y
yv
x
x
y
yv
Im(f )
01. Obtenha as coordenadas do vértice da parábola cor-
respondente à função quadrática definida, no con-
junto dos números reais, por y = f(x) = – 2x2 + 4x.
• A partir dos coeficientes da função quadrática e
das relações apresentadas, temos:
x
b
a
xv v= = ⇒ =− − . −2
4
2 2
1
( )
y
a
yv v= = ⇒ =− −
− . − .
. −
Δ
4
4 4 2 0
4 2
2
2 ( )
( )
• Para o cálculo da ordenada, também podemos
fazer:
yv = f(xv)
yv = f(1) = – 2 ∙ 1
2 + 4 ∙ 1 ⇒ yv = 2
02. Obtenha as coordenadas do ponto em que a parábola
correspondente ao gráfico da função quadrática
y = f(x) = 3x2 + 4x – 7 intersecta o eixo das ordenadas.
• No eixo das ordenadas, temos que a abscissa é
igual a zero. Assim, para obter a ordenada, basta
substituir x por zero:
x = 0 ⇒ y = f(0)
y = 3 ∙ 02 + 4 ∙ 0 – 7 ⇒ y = – 7
• O termo independente de x indica a ordenada
do ponto em que o gráfico intersecta o eixo das
ordenadas.
03. Obtenha os zeros da função quadrática definida por
y = f(x) = x2 + 6x – 7 e as coordenadas dos pontos onde a
parábola correspondente intersecta o eixo das abscissas.
• Para obter as coordenadas dos pontos em que a
parábola intersecta o eixo das abscissas, fazemos:
y = 0
x2 +6x – 7 = 0
x = ±− −
. . −
.
6 4 1
2 1
6 72 ( )
x
x
x
= ± →
= ⇒
= ⇒
⎧
⎨
⎩
− − −6
2
8 7 7 0
1 1 0
( ; )
( ; )
x = 1 e x = –7 são os zeros dessa função.
04. Na função quadrática do exemplo anterior, obtenha as
coordenadas do vértice da parábola correspondente.
• Como o vértice está no eixo de simetria, sua
abscissa pode ser obtida pela média aritmética
dos zeros da função:
x
x x
xv v=
+ = + ⇒ =1 2 7 1
2
3
2
− −
• A ordenada é a imagem da abscissa do vértice,
ou seja:
yv = f(xv)
yv = f(– 3) = (– 3)
2 + 6 ∙ (– 3) – 7 ⇒ yv = – 16
Situações resolvidas
01. Dada uma função real quadrática da forma f x ax bx c( )= + +2 , sendo a, b e c números reais (com a diferente de
zero), obtenha a abscissa do vértice da parábola correspondente.
02. A partir da abscissa do vértice da parábola, correspondente ao gráfico da função quadrática f x ax bx c( )= + +2 ,
obtenha a ordenada do vértice.
03. Em relação à função quadrática definida por f x x x( ) ,= − + −2 6 12 obtenha as coordenadas do vértice da parábola
correspondente e o conjunto imagem dessa função.
04. (FGV – SP) – Uma parede de tijolos será usada como um dos lados de um curral retangular. Para os outros lados,
iremos usar 400 metros de tela de arame, de modo a produzir uma área máxima. Determine as medidas do curral
e a área máxima que ele pode ter.
Situações para resolver
30 Extensivo Terceirão
Aula 08
31Matemática 2A
Testes
Assimilação
08.01. O gráfico a seguir pertence a uma função quadrática
f(x) = ax2 + bx +c, com domínio e contradomínio no conjunto
dos números reais. A respeito dessa função, assinale o que
for correto.
y
x
321–1–2–3 0
3
8
–1
01) O coeficiente “a” dessa função é positivo.
02) O valor do coeficiente “c”, nessa função, é igual a –1
04) f(–2) + f(3) = 11
08) O vértice dessa função possui as coordenadas (–1, 0).
16) As raízes de f são –1 e 1.
32) O discriminante dessa função é igual a zero.
08.02. (UF. OURO PRETO – MG) – Em relação ao gráfico da
função f(x) = – x2 + 4x – 3, pode−se afirmar que:
a) é uma parábola de concavidade voltada para cima;
b) seu vértice é o ponto V(2, 1);
c) intercepta o eixo das abscissas em P(–3, 0) e Q(3, 0);
d) o seu eixo de simetria é o eixo das ordenadas;
e) intercepta o eixo das ordenadas em R(0, 3).
08.03. (U. E. FEIRA DE SANTANA – BA) – Considerando-se
a função real f(x) = –2x2 + 4x + 12, o valor máximo desta
função é:
a) 1
b) 3
c) 4
d) 12
e) 14
08.04. Considerando-se a função real f(x) =
3
8
17 222x x ,
o valor do domínio que resulte no valor máximo desta fun-
ção é:
a) 31
8
b) 17
8
c) 68
3
d)
44
3
e) 4
Aperfeiçoamento
08.05. (PUC – SP) – A função quadrática
y = (m2 – 4)x2 – (m + 2) x – 1 está definida quando:
a) m = 4
b) m≠4
c) m ≠ ±2
d) m = ± 2
08.06. (UEL – PR) – A função real f, de variável real, dada por
f(x) = –x2 + 12x + 20, tem um valor:
a) mínimo, igual a –16, para x = 6
b) mínimo, igual a 16, para x = – 12
c) máximo, igual a 56, para x = 6
d) máximo, igual a 72, para x = 12
e) máximo, igual a 240, para x = 20
32 Extensivo Terceirão
08.07. (PUC – RS) – O morro onde estão situadas as emis-
soras de TV em Porto Alegre pode ser representado grafi-
camente, com algum prejuízo, em um sistema cartesiano,
através de uma função polinomial de grau 2 da forma
y = ax2 + bx + c com a base da montanha no eixo das
abscissas.
Para que fique mais adequada essa representação, devemos
ter:
a) a > 0 e b2 – 4ac > 0
b) a > 0 e b2 – 4ac < 0
c) a < 0 e b2 – 4ac < 0
d) a < 0 e b2 – 4ac > 0
e) a < 0 e b2 – 4ac = 0
08.08. (UFPB) – O gráfico da função
y = f(x) = – (1/200)x2 + (1/5)x, representado na figura a
seguir, descreve a trajetória de um projétil, lançado a partir
da origem.
H
0 x (km)
y = f(x)
y (km)
A
Sabendo-se que x e y são dados em quilômetros, a altura
máxima H e o alcance A do projétil são, respectivamente,
a) 2 km e 40 km. b) 40 km e 2 km.
c) 2 km e 10 km. d) 10 km e 2 km.
e) 2 km e 20 km.
08.09. (UERN) – Se o ponto (k, 9) representa o vértice da pa-
rábola determinada pela função quadrática y = 6x2 + bx +15,
então o valor da incógnita b é:
a) 6 b) 7 c) 12 d) 13
08.10. (FAAP – SP) – Uma companhia estima que pode ven-
der mensalmente q milhares de unidades de seu produto ao
preço de p reais por unidade. A receita mensal das vendas é
igual ao produto do preço pela quantidade vendida. Supondo
p = –0,5q + 10, quantos milhares de unidades deve vender
mensalmente para que a receita seja a máxima possível?
a) 18
b) 20
c) 5
d) 10
e) 7
Aprofundamento
08.11. (UNESPAR – PR) – Dadas as funções f(x) = 2x2 + 2x – 4
e g(x) = 12x2 + 12x – 24, analise as afirmações a seguir:
I. O gráfico de f tem concavidade voltada para cima e o
gráfico de g tem concavidade voltada para baixo;
II. A função f tem raízes e vértice iguais às raízes e vértice
da função g;
III. A função f tem raízes iguais às raízes de g porém os
vértices das duas funções são diferentes.
Com base nas informações anteriores responda:
a) Apenas I é verdadeira;
b) Apenas II é verdadeira;
c) Apenas III é verdadeira;
d) I e II são verdadeiras;
e) I e III são verdadeiras.
Aula 08
33Matemática 2A
08.12. (FAMERP – SP) – A figura representa o desenho da
arcada dentária de um animal, feito no plano cartesiano
ortogonal em escala linear.
y
2
–4 –2 0 2 4 x
8
Sabendo que as posições dos centros dos dentes destacados
em cinza nessa arcada são modeladas nesse plano por meio
da função quadrática y = ax2 + b, então a + b é igual a:
a) 8,5.
b) 9,2.
c) 9,5.
d) 10,2.
e) 9,0.
08.13. (FGV – SP) – Para que valor de a o conjunto ima-
gem da função quadrática f(x) = ax2 – 4x + 6 é o intervalo
− ∞[ [6, ?
a)
1
7
c)
1
5
e)
1
3
b)
1
6
d)
1
4
08.14. (ESPM – SP) – O gráfico abaixo representa uma função
quadrática y = f(x). O valor de f(–6) é:
y
x
2
1
3
a) 74
b) 63
c) 42
d) 51
e) 37
08.15. (UFPR) – Um retângulo no plano cartesiano possui
dois vértices sobre o eixo das abscissas e outros dois vértices
sobre a parábola de equação y = 4 – x2, com y > 0. Qual é o
perímetro máximo desse retângulo?
y
y = 4 – x2
x
a) 4.
d) 12.
b) 8.
e) 17.
c) 10.
34 Extensivo Terceirão
08.16. (VUNESP – SP) – Uma função quadrática f é dada por
f(x) = x2 + bx + c, com b e c reais. Se f(1) = –1 e f(2) – f(3) = 1,
o menor valor que f(x) pode assumir, quando x varia no
conjunto dos números reais, é igual a:
a) –12 b) –6 c) –10 d) –5 e) –9
08.17. (UFRRJ) – O custo de produção de um determi-
nado artigo é dado por C(x) = 3x2 – 15x + 21. Se a venda
de x unidades é dada por V(x) = 2x2 + x, para que o lucro
L(x) = V(x) – C(x) seja máximo, devem ser vendidas:
a) 20 unidades
b) 16 unidades
c) 12 unidades
d) 8 unidades
e) 4 unidades
08.18. (CMRJ) – Uma ponte metálica, em forma de arco de
parábola, será construída. Sua sustentação será feita com
seis pendurais metálicos, três de cada lado, distando 30 m
um do outro, como ilustra a figura abaixo. Sabendo que a
ponte tem 40 m de altura, quantos metros de pendurais serão
necessários para a construção desta ponte?
30
30
30
30
PENDURAIS
a) 120 m b) 140 m c) 160 m d) 180 m e) 200 m
Desafio
08.19. (PUCCAMP – SP) – A soma e o produto das raízes
de uma função do 2º grau são, respectivamente, 6 e 5. Se o
valor mínimo dessa função é –4, então seu vértice é o ponto
a) (3, –4)
b)
11
2
4, −⎛
⎝
⎜
⎞
⎠
⎟
c) (0, –4)
d) (–4; 3)
e) (–4, 6)
08.20. (UNESP – SP) – Em relação a um sistema cartesiano
de eixos ortogonais com origem em O (0, 0), um avião se
desloca, em linha reta, de O até o ponto P, mantendo sempre
um ângulo de inclinação de 45° com a horizontal. A partir
de P, o avião inicia trajetória parabólica, dada pela função
f(x) = –x2 + 14x – 40, com x e f(x) em quilômetros. Ao atingir
o ponto mais alto da trajetória parabólica, no ponto V, o avião
passa a se deslocar com altitude constante em relação ao
solo, representado na figura pelo eixo x.
V
(km)
x
P
0
O
Solo
y = f(x)
A
lti
tu
de
(k
m
)
45°
Em relação ao solo, do ponto Ppara o ponto V, a altitude do
avião aumentou
a) 2,5 km. b) 3 km. c) 3,5 km. d) 4 km. e) 4,5 km.
Aula 08
35Matemática 2A
Gabarito
08.01. 23(01 + 02 + 04 + 16)
08.02. b
08.03. e
08.04. c
08.05. c
08.06. c
08.07. d
08.08. a
08.09. c
08.10. d
08.11. c
08.12. c
08.13. e
08.14. d
08.15. c
08.16. d
08.17. d
08.18. e
08.19. a
Se a soma das raízes é 6 e o produto das raízes é 5 então uma
possível função
Soma = 6 = 6 b = 6a
Produto = 5 = 5 c = 5a
f(
→ →
→ →
⎫
⎬
⎪⎪
⎭
⎪
⎪
− −b
a
c
a
xx) = ax 6a 2 − + 5a
Como x = = = 3 e y = v v
b
a
a
a2
6
2
4 (valor mínimo dessa fun-
ção), temos V(3; –4)
08.20. d
Observe a gráfico abaixo.
V
(km)
x
0
O
Solo
y = f(x)
A
lti
tu
de
(k
m
)
45°
B
(X : X)
Calculando x : x = = = 7
Calculando y : y
v v
v v
⇔
⇔
− −
−
b
a2
14
2
= f(7) = 7 + 14 72 ⋅ =− 40 9
O ponto P tem abscissa e ordenada de valores iguais, pois o triân-
gulo OPB é isósceles e retângulo em B. Sendo assim vamos consi-
derar P(x; x). Como a reta OP
� ��
corresponde ao gráfico da função
definida por g(x) = x, temos:
f x g x x x x
x x
x x
( ) ( )
.
= ⇔ − + − =
⇔ − + =
⇔ = =
2
2
14 40
13 40 0
5 8 ou
Como x < 7 pois xv = 7, então x = 5.
Portanto, (ordenada do vértice V)
(ordenada do vértice V) = 9 – 5 = 4Km
36 Extensivo Terceirão
Anotações




