
Faculdade
Uninassau
Disciplina
Equações
Diferencia
is
Curso
Engenharia
Professor
a
Rafaela Andrade
Alunos
Lista de Equações Diferenciais - 1 Unidade
2019.1
Obs: A lista de exercício só será considerada para correção ref erente aos pontos
complementares da 1 nota, se entregue com todas as qu estões acompa nhadas dos
devidos cálculos.
1. Encontrar o intervalo de convergência das seguintes séries de pot ências:
2. Os valores de x para os quais a série de potência a seguir seja convergente é:
a) x = 0
b) x = 4
c) x = 1
d) x = infinito
e) Para todo x.
3. Encontrar uma representação por série de potências de x para as seguintes funções:
4. Avalie a integral indefinida ∫ e-x²dx como uma série infinita. (Dica: Aplique o
conceito de integração termo a termo).
5. Encontre a série de Ta yl or para f(x) centrada no valor da do a e determine seu raio
de convergência:
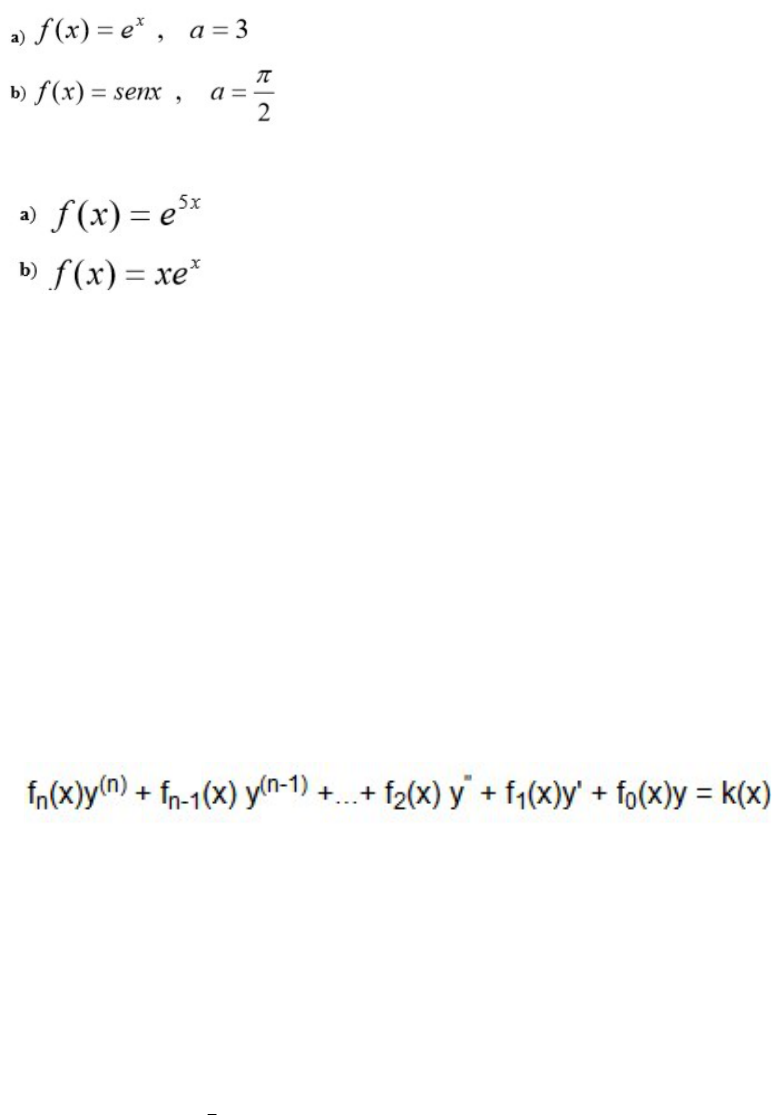
6. Encontre a série de Maclaurin para f(x) abaixo e determine seu raio de conver gência:
7. Sobre conceitos de e quações diferenciais, julgu e os it ens como V (verdadeir o) ou (F)
falso. No caso dos itens falsos, CORR IJ A-OS.
( ) Chamamos de equações diferencias, equa ções que apresentam derivadas ou
diferenciais de uma função desconhecida (a incó gnita da equação).
( ) Uma classificação importante baseia-se em se a função desconh ecida depende
de uma única variável independente ou de div ersas variáveis independentes. No
primeiro caso, aparecem apenas variáveis independentes na equação dife rencial, e ela
é dita uma equação diferencial ordinári a. Nestas não há derivadas. Já no segundo
caso, as equações sã o apresentadas com v ariáveis e suas derivadas. Esta é chamada
de uma equação diferencial parcial.
( ) A o rdem de uma equação diferencial é a ordem do maior grau da ex ponencial
da variável dependente que aparece na equaç ão.
( ) Uma classificação de equações diferenciais é se elas são lineares ou não. A
equação diferencial ordinária é dita linear se F é u ma função do tipo:
onde k(x) e os coeficientes fi (x ) são funções de x.
( ) Quanto a solução, pode ser classificada como solução geral - apresenta n
variáveis independentes entre si (n = ordem da EDO) e séries de potências. E solução
particular - obtida da geral, mediante condições dadas (chamadas co ndições iniciais
ou condições de contorno).
8. Verifique se a função dada é solução para a equação diferencial. ( 1
c e 2
c são
constantes)
a) 2
,0'2
x
eyyy
b)
1,'' 3 xyyxyy
c) xx ececyyyy 4
2
3
1
,012'''
d) xcyyy 5cos,025'' 1
9. Encontre valores de
m
para que xm
ey é solução da equação
.025'10''
yyy
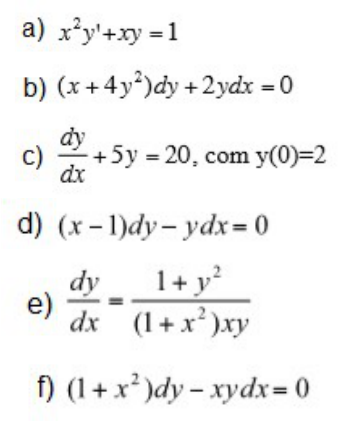
10. Quais das seguintes funções são soluções da equa ção diferencial y'' - y = 0?
I. y(x ) = ex
II. y(x) = senx
III. y(x) = 4e-x
IV. y(x) = (1/2)x2 + 1
a) Apensas I.
b) Apensas I e II.
c) Apenas I e III.
d) Apensas III e IV
e) Nenhuma das funções.
11. Determine c1 e c2 de modo que y(x) = c1e2x + c2ex + 2senx satisf aça as condições
y(0) = 0 e y′(0) = 1.
a) c1 = c2 = -1
b) c1 = - 1 e c2 = 1
c) c1 = sen x e c2 = cos x
d) c1 = c2 = 1
e) c1 = -4 e c2 = 3
12. Quais das seguintes funções são soluções da equa ção diferencial y′ – 5y = 0?
a) y = 5x
b) y = x5
c) y = e5x
d) y = 2e5x
e) y = 5e2x
13. Resolva as seguintes Equ ações Lineares de 1ª ordem:
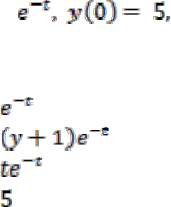
14. Sendo a velocidade expressa por v (t)=9,8 - 9,8e-t . A partir da solução da EDO da
velocidade e sabendo qu e a posição inicial é s(0)=0, qual o valor aproxi mado de s
passados quatro se gundos? Obs.: Essa função, com s(0)=0, vai acabar nos
mostrando o deslocamento.
a) 9,8m
b) 29,58m
c) 39,02m
d) 48,82m
e) 49,18m
15. Determinando explicitamente a solução do problema de valor inicial de
y’ + y = obtemos:
a) (t + 5) e-t
b)
c)
d)
e) t
Bons estudos!
Prévia do material em texto
Faculdade Uninassau Disciplina Equações Diferenciais Curso Engenharia Professora Rafaela Andrade Alunos Lista de Equações Diferenciais - 1 Unidade 2019.1 Obs: A lista de exercício só será considerada para correção referente aos pontos complementares da 1 nota, se entregue com todas as questões acompanhadas dos devidos cálculos. 1. Encontrar o intervalo de convergência das seguintes séries de potências: 2. Os valores de x para os quais a série de potência a seguir seja convergente é: a) x = 0 b) x = 4 c) x = 1 d) x = infinito e) Para todo x. 3. Encontrar uma representação por série de potências de x para as seguintes funções: 4. Avalie a integral indefinida ∫ e-x²dx como uma série infinita. (Dica: Aplique o conceito de integração termo a termo). 5. Encontre a série de Taylor para f(x) centrada no valor dado a e determine seu raio de convergência: 6. Encontre a série de Maclaurin para f(x) abaixo e determine seu raio de convergência: 7. Sobre conceitos de equações diferenciais, julgue os itens como V (verdadeiro) ou (F) falso. No caso dos itens falsos, CORRIJA-OS. ( ) Chamamos de equações diferencias, equações que apresentam derivadas ou diferenciais de uma função desconhecida (a incógnita da equação). ( ) Uma classificação importante baseia-se em se a função desconhecida depende de uma única variável independente ou de diversas variáveis independentes. No primeiro caso, aparecem apenas variáveis independentes na equação diferencial, e ela é dita uma equação diferencial ordinária. Nestas não há derivadas. Já no segundo caso, as equações são apresentadas com variáveis e suas derivadas. Esta é chamada de uma equação diferencial parcial. ( ) A ordem de uma equação diferencial é a ordem do maior grau da exponencial da variável dependente que aparece na equação. ( ) Uma classificação de equações diferenciais é se elas são lineares ou não. A equação diferencial ordinária é dita linear se F é uma função do tipo: onde k(x) e os coeficientes fi (x) são funções de x. ( ) Quanto a solução, pode ser classificada como solução geral - apresenta n variáveis independentes entre si (n = ordem da EDO) e séries de potências. E solução particular - obtida da geral, mediante condições dadas (chamadas condições iniciais ou condições de contorno). 8. Verifique se a função dada é solução para a equação diferencial. ( 1c e 2c são constantes) a) 2,0'2 x eyyy b) 1,'' 3 xyyxyy c) xx ececyyyy 42 3 1,012''' d) xcyyy 5cos,025'' 1 9. Encontre valores de m para que xmey é solução da equação .025'10'' yyy 10. Quais das seguintes funções são soluções da equação diferencial y'' - y = 0? I. y(x) = ex II. y(x) = senx III. y(x) = 4e-x IV. y(x) = (1/2)x2 + 1 a) Apensas I. b) Apensas I e II. c) Apenas I e III. d) Apensas III e IV e) Nenhuma das funções. 11. Determine c1 e c2 de modo que y(x) = c1e2x + c2ex + 2senx satisfaça as condições y(0) = 0 e y′(0) = 1. a) c1 = c2 = -1 b) c1 = - 1 e c2 = 1 c) c1 = sen x e c2 = cos x d) c1 = c2 = 1 e) c1 = -4 e c2 = 3 12. Quais das seguintes funções são soluções da equação diferencial y′ – 5y = 0? a) y = 5x b) y = x5 c) y = e5x d) y = 2e5x e) y = 5e2x 13. Resolva as seguintes Equações Lineares de 1ª ordem: 14. Sendo a velocidade expressa por v(t)=9,8 - 9,8e-t. A partir da solução da EDO da velocidade e sabendo que a posição inicial é s(0)=0, qual o valor aproximado de s passados quatro segundos? Obs.: Essa função, com s(0)=0, vai acabar nos mostrando o deslocamento. a) 9,8m b) 29,58m c) 39,02m d) 48,82m e) 49,18m 15. Determinando explicitamente a solução do problema de valor inicial de y’ + y = obtemos: a) (t + 5) e-t b) c) d) e) t Bons estudos!








