w ww .ma te ma ti que s. com. br
Ma temá tic a Básica
10ª L is ta de Ex er c íc ios – Núm eros C omp le xo s
1. Calc ule o núm ero complexo i126 + i
-1 26 + i
31 - i 180
2. Sendo z = 5i + 3i2 - 2i3 + 4i 27 e w = 2i
12 - 3i
15 ,
c alc ule Im (z ).w + Im (w ).z .
3. (UC MG) O núm ero c omplexo 2z , tal que 5z + = 12 + 6i é:
4. (UCSal) Para que o produto (a + i) . (3 - 2i) seja real, a dev e s er:
5. (UFBA) Sen do a = -4 + 3i , b = 5 - 6 i e c = 4 - 3i , o valor de ac +b é:
6. (Mac kenz ie-SP) O valor da expres s ão y = i + i2 + i
3 + ... + i
10 01 é:
7. Determine o núm ero natural n t al que ( 2i)n + (1 + i)2n + 16i = 0. Resp: 3
8. Calc ule [(1 + i)80 + (1 + i)82] : i96
.240. Res p: 1 + 2i
9. Se os núm eros c omplexos z e w s ão tais que z = 2 - 5i e w = a + bi, sabendo-s e que z + w é um núm ero
real e z .w .é um im aginário puro , pe de-s e calc ular o valor de b 2 - 2a. Res p: 50
10. Se o núm ero c omplexo z = 1 - i é uma das raíz es da equaç ão x10 + a = 0, ent ão c alc ule o va lor de a.
Resp: 32i
11. D eterm ine o núm ero com plexo z tal que iz + 2. + 1 - i = 0.
12. (UF MG) Se
is enθcosθrz
é um núm ero c om plexo na form a trigonom étrica, m os tra-s e que
nθis ennθcosrz nn
para todo n N. Es s a fórm ula é c onhec ida com o fórm ula de De Moi vre.
A) Demons tre a fórm ula de De Moivre para n = 2, ou seja, dem onstre que
θ2is enθ2cosrz 22
.
B) Determ ine todos os valores de n, n N, para os quais
n
i3
seja imaginário puro.
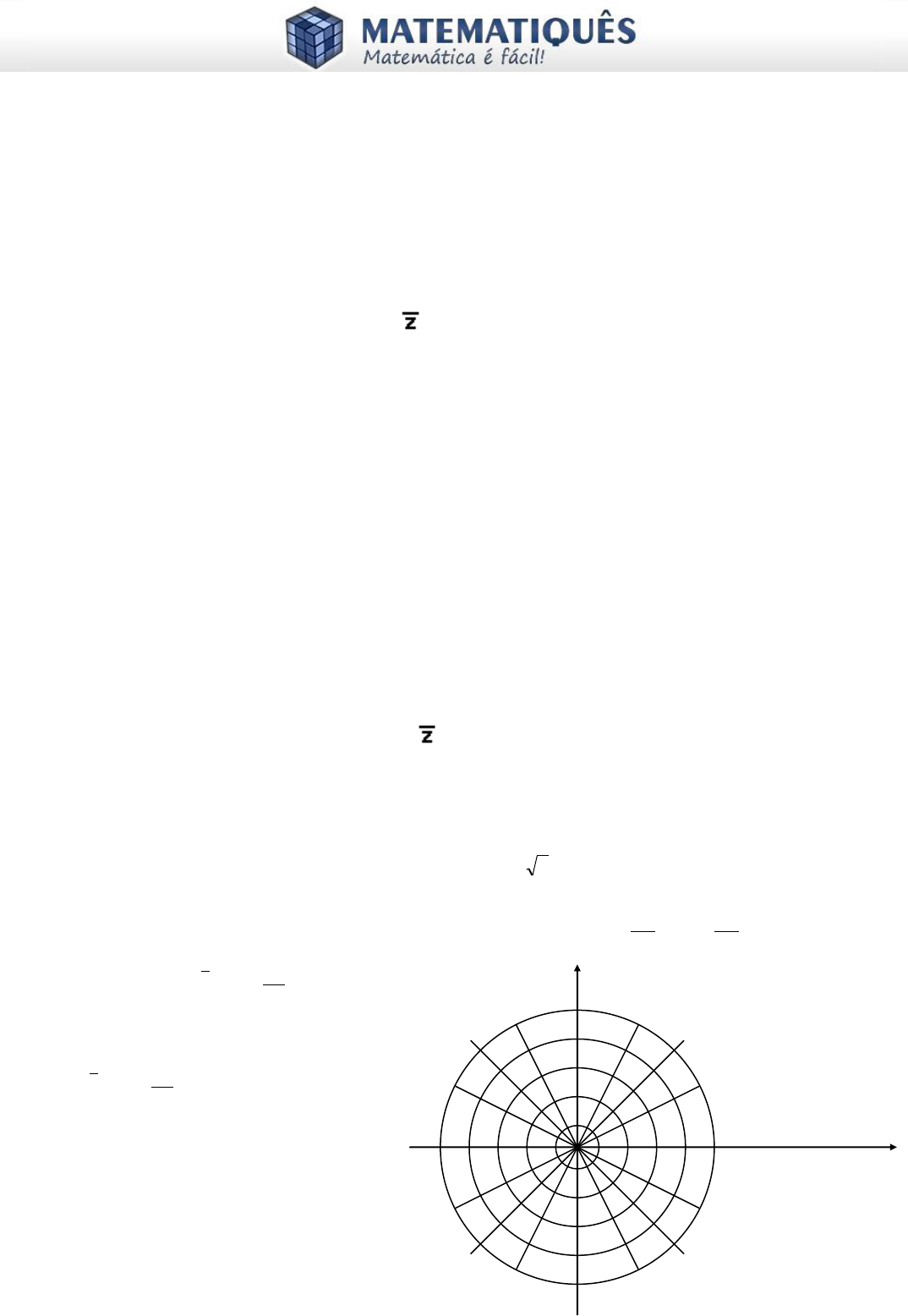
13. (UF MG) A) Dado o núm ero c omplexo na form a trigonom étric a
8
3
s en
8
3
cos2
iz
, es c reva os
núm eros c om plexos
z
, z 2 e
z
10
na form a trigonom étric a.
B) No pla no c omplexo da fi gura ao lado,
m arque e ident ifique os núm eros
z ,
z
, z 2 e
z
10
no item ac ima.
Ness a figura, os ângulos form ados por dois
raios cons ec utivos quaisquer têm a
m esm a m edida.
Eixo im aginário
Eixo real
5
3
w ww . ma te ma tique s. com. br
14. (UF MG) Por três pontos não-c olineares do pla no c om plexo, z 1, z 2 e z 3, pas s a um a únic a c irc unferência.
Sabe-s e que um ponto z está s obre ess a c irc unferência s e, e s om ente s e,
zzzzzzzz 2
1
31
32
for um núm ero real.
Seja C a únic a c ircunferênc ia que pass a pelos pontos z 1 = 1, z2 = -3i e z 3 = -7 + 4i do plano c om plexo.
As s im s endo, determine todos os pontos do plano c om plexo cuja parte real é igua l a –1 e que estão
s obre a c irc unferênc ia C.
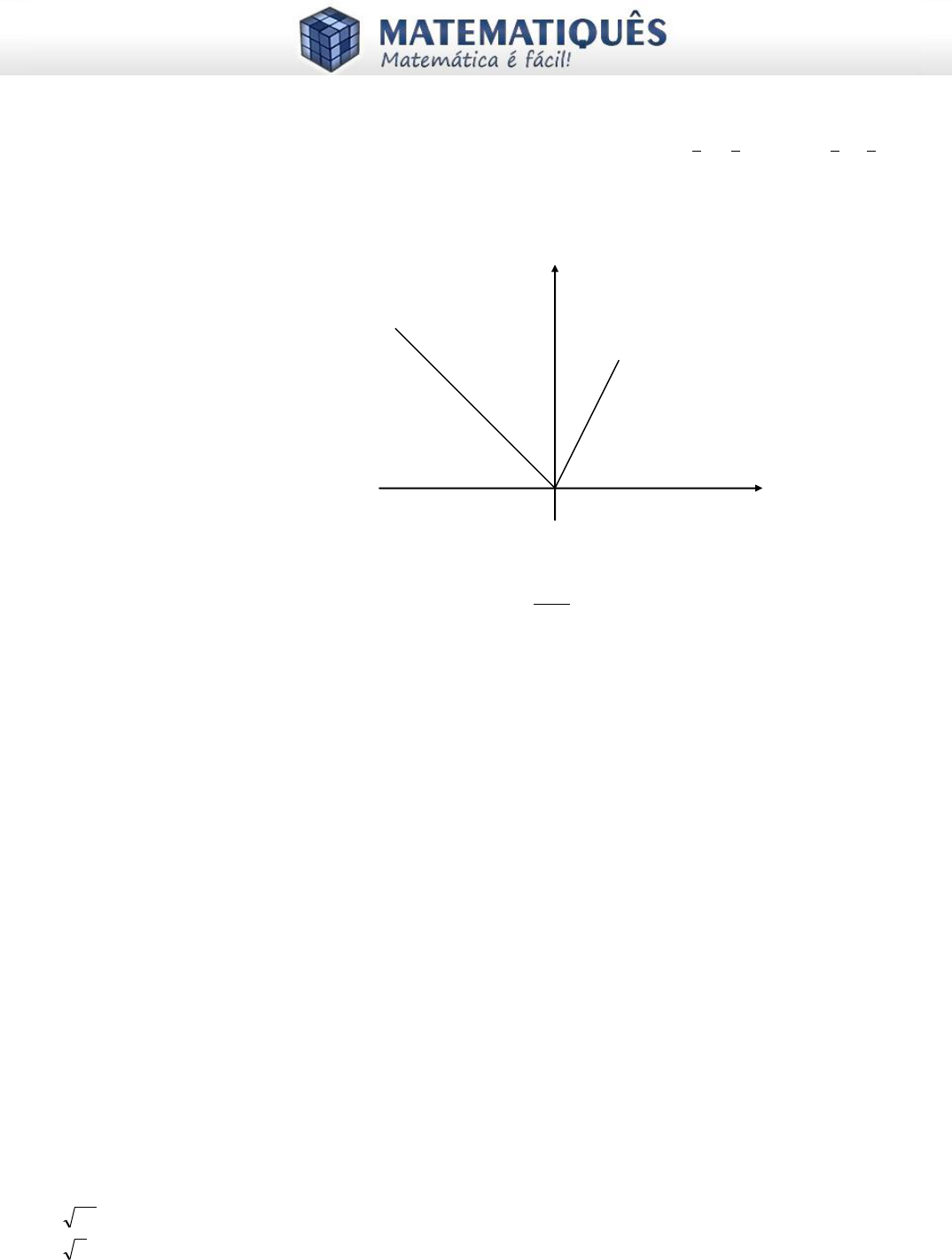
15 – (UF MG) 2002 - O bs erve esta figura:
Ness a figura, OP = 2 e OQ = 4.
Sejam z e w, respec tivamente, os núm eros c omplexos repres entados geom etric amente pelos pontos P
e Q.
Cons iderando es s es dados , es c reva o núm ero c om plexo
5
11
.wi
z
na form a a + bi, em que a e b s ão
núm eros reais.
16. (UEFS) O valor da e xpres s ão E = x-1 + x
2, para x = 1 - i , é:
a) -3i
b)1-i
c ) 5/2 + (5/2)i
d) 5/2 - (3/2)i
e) ½ - (3/2)i
17. (UEFS) Sim plific ando-s e a expres s ão E = i7 + i
5 + ( i
3 + 2i
4 )2 , o btêm -s e:
a) -1+2i
b) 1+2i
c ) 1 - 2i
d) 3 - 4i
e) 3 + 4i
18. (UEFS) Se m - 1 + ni = (3+i).(1 + 3i), então m e n são res pec tivam ente:
a) 1 e 10
b) 5 e 10
c ) 7 e 9
d) 5 e 9
e) 0 e -9
19. (UEFS) A s oma de um núm ero complexo z c om o triplo do s eu c onjugado é igual a -8 - 6i. O módulo de z
é:
a)
13
b)
7
c ) 13
d) 7
e) 5
Q
y
P
x
44°
65°
0

w ww . ma te ma tique s. com. br
GAB ARIT O:
1) -3 - i
2) -3 + 18i
3) 4 + 3i
4) 3/2
5) -2 + 18i
6) i
7) 3
8) 1 + 2i
9) 50
10) 32i
11) -1 - i
14) –1 + 4i e -1 – 4i
16) B
17) D
18) A
19) A
20) A
21) E
20. (FESP/UPE) Seja z = 1+i , onde i é a un idade im aginária. Pod emos afirmar que z 8 é igual a:
a) 16
b) 161
c ) 32
d) 32i
e) 32+16i
21. (UC Sal)Sabendo que (1+ i)2 = 2i, e ntão o valor d a expres s ão y = (1+i) 48 - (1+i)49 é:
a) 1 + i
b) -1 + i
c ) 2
24 . i
d) 2
48 . i
e) -2
24 . i
Prévia do material em texto
�� Matemática Básica 10ª Lista de Exercícios – Números Complexos 1. Calcule o número complexo i126 + i-126 + i31 - i180 2. Sendo z = 5i + 3i2 - 2i3 + 4i27 e w = 2i12 - 3i15 , calcule Im(z).w + Im(w).z . 3. (UCMG) O número complexo 2z, tal que 5z + 4. (UCSal) Para que o produto (a + i) . (3 - 2i) seja real, a deve ser: 5. (UFBA) Sendo a = -4 + 3i , b = 5 - 6i e c = 4 - 3i , o valor de ac+b é: 6. (Mackenzie-SP) O valor da expressão y = i + i2 + i3 + ... + i1001 é: 7. Determine o número natural n tal que (2i)n + (1 + i)2n + 16i = 0. Resp: 3 8. Calcule [(1 + i)80 + (1 + i)82] : i96.240. Resp: 1 + 2i 9. Se os números complexos z e w são tais que z = 2 - 5i e w = a + bi, sabendo-se que z + w é um número real e z.w .é um imaginário puro , pede-se calcular o valor de b2 - 2a. Resp: 50 10. Se o número complexo z = 1 - i é uma das raízes da equação x10 + a = 0, então calcule o valor de a. Resp: 32i 11. Determine o número complexo z tal que iz + 2. + 1 - i = 0. 12. (UFMG) Se é um número complexo na forma trigonométrica, mostra-se que para todo n ( N. Essa fórmula é conhecida como fórmula de De Moivre. Demonstre a fórmula de De Moivre para n = 2, ou seja, demonstre que . Determine todos os valores de n, n ( N, para os quais seja imaginário puro. 13. (UFMG) A) Dado o número complexo na forma trigonométrica , escreva os números complexos , z2 e na forma trigonométrica. No plano complexo da figura ao lado, marque e identifique os números z, , z2 e no item acima. Nessa figura, os ângulos formados por dois raios consecutivos quaisquer têm a mesma medida. 14. (UFMG) Por três pontos não-colineares do plano complexo, z1, z2 e z3, passa uma única circunferência. Sabe-se que um ponto z está sobre essa circunferência se, e somente se, for um número real. Seja C a única circunferência que passa pelos pontos z1 = 1, z2 = -3i e z3 = -7 + 4i do plano complexo. Assim sendo, determine todos os pontos do plano complexo cuja parte real é igual a –1 e que estão sobre a circunferência C. 15 – (UFMG) 2002 - Observe esta figura: Nessa figura, OP = 2 e OQ = 4. Sejam z e w, respectivamente, os números complexos representados geometricamente pelos pontos P e Q. Considerando esses dados, escreva o número complexo na forma a + bi, em que a e b são números reais. 16. (UEFS) O valor da expressão E = x-1 + x2, para x = 1 - i , é: a)-3i b)1-i c) 5/2 + (5/2)i d) 5/2 - (3/2)i e) ½ - (3/2)i 17. (UEFS) Simplificando-se a expressão E = i7 + i5 + ( i3 + 2i4 )2 , obtêm-se: a) -1+2i b) 1+2i c) 1 - 2i d) 3 - 4i e) 3 + 4i 18. (UEFS) Se m - 1 + ni = (3+i).(1 + 3i), então m e n são respectivamente: a) 1 e 10 b) 5 e 10 c) 7 e 9 d) 5 e 9 e) 0 e -9 19. (UEFS) A soma de um número complexo z com o triplo do seu conjugado é igual a -8 - 6i. O módulo de z é: a) b) c) 13 d) 7 e) 5 20. (FESP/UPE) Seja z = 1+i , onde i é a unidade imaginária. Podemos afirmar que z8 é igual a: a) 16 b) 161 c) 32 d) 32i e) 32+16i 21. (UCSal)Sabendo que (1+i)2 = 2i, então o valor da expressão y = (1+i)48 - (1+i)49 é: a) 1 + i b) -1 + i c) 224 . i d) 248 . i e) -224 . i Eixo imaginário 3 5 Eixo real 0 65° 44° x P y Q GABARITO:��1) -3 - i �2) -3 + 18i �3) 4 + 3i �4) 3/2 �5) -2 + 18i �6) i �7) 3 �8) 1 + 2i �9) 50 �10) 32i �11) -1 - i 14) –1 + 4i e -1 – 4i 16) B �17) D �18) A �19) A �20) A �21) E _1075010580.unknown _1075010988.unknown _1075015023.unknown _1075033277.unknown _1075011022.unknown _1075010790.unknown _1075010218.unknown _1075010485.unknown _1075009274.unknown _1075010102.unknown _1075009212.unknown










