Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
1
Hidráulica Geral
Segunda Lista de Exercícios
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
2
1) [6.1] Uma bomba centrífuga, com as características Hm
x Q mostradas no quadro a
seguir, produziu 50 l/s, quando foi instalada nu ma adutor a que interliga dois
reservatórios cuja diferença entre os níveis de água é 30,0 m. Após 20 anos de
funcionamento deste sistema, verificou-se que a vazão havia sido reduzida para 40 l/s
devido ao aumento da perda de carga na tubulação. Desprezando as perdas de carga
localizadas, pede -se determinar, após 20 anos de uso, a perda de carga contínua na
tubulação e o aumento percentual do coeficiente de perda de carga da fórmula
Universal.
Q (l/s)
0,0
10,0
20,0
30,0
40,0
50,0
60,0
70,0
80,0
Hm (m)
80,0
75,1
69,6
63,6
57,1
50,0
42,4
34,3
25,6
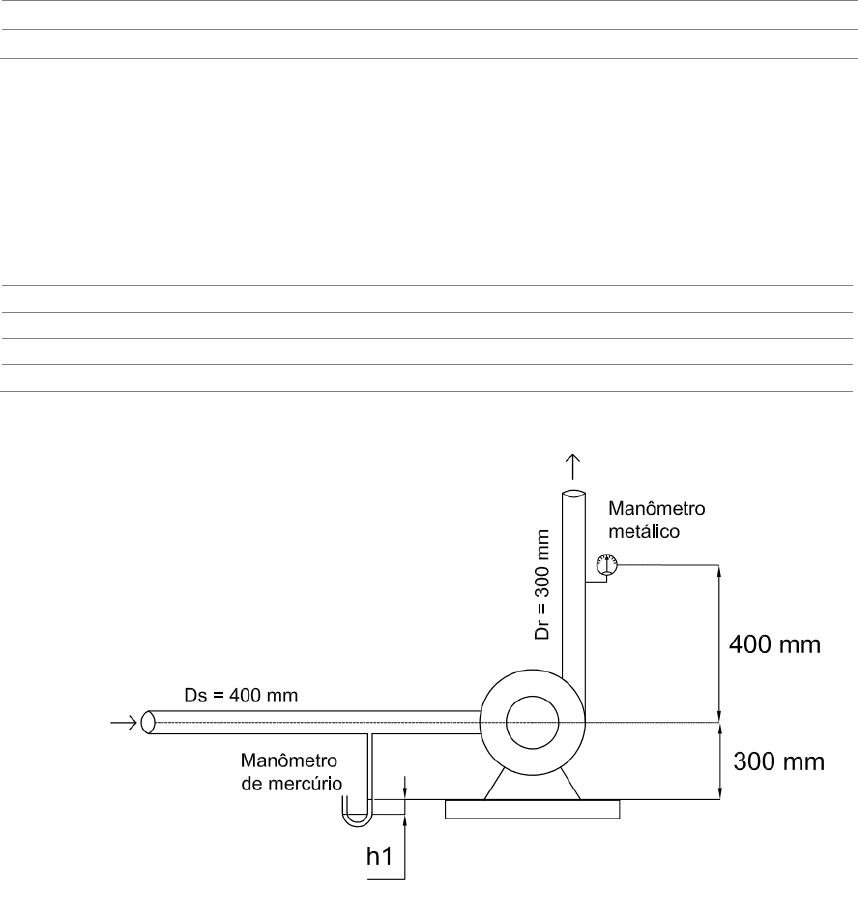
2) [6.2] Uma bomba centrífuga foi testada em laboratório numa instalação cujo esquema de
medição de pressão é mostrado na figura abaixo. As informações obtidas nos testes
estão no quadro a seguir. Pede-se determinar a curva característica Hm x Q da bomba.
Teste
Vazão (l/s)
Manômetro de mercúrio h1 (mm)
Manômetro metálico P2 (k Pa)
1
40,0
120
490
2
70,0
160
372
3
100,0
190
245
3) [6.3] Uma bomba testada em laboratório apresentou as características mostradas no
quadro a seguir. Esta bomba deverá ser utilizada numa est ação elevatória cuja altura
geométrica é 25 m, ligada a uma adutora com coeficiente de perda de carga da fórmula
Universal igual a 0,025 e extensão de 3556 m. As pe ças, conexões e aparelhos
provocam uma perda de carga localizada de 10 U2/2g. Pede-se selecionar o diâmetro da
tubulação para permitir o escoamento de 80 l/s e calcular a potência consumida.
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
3
Vazão (l/s)
0
20
40
60
80
100
120
Altura manométrica (m)
60
59
57
52
45
35
22
Eficiência (%)
-
42
58
71
75
69
54
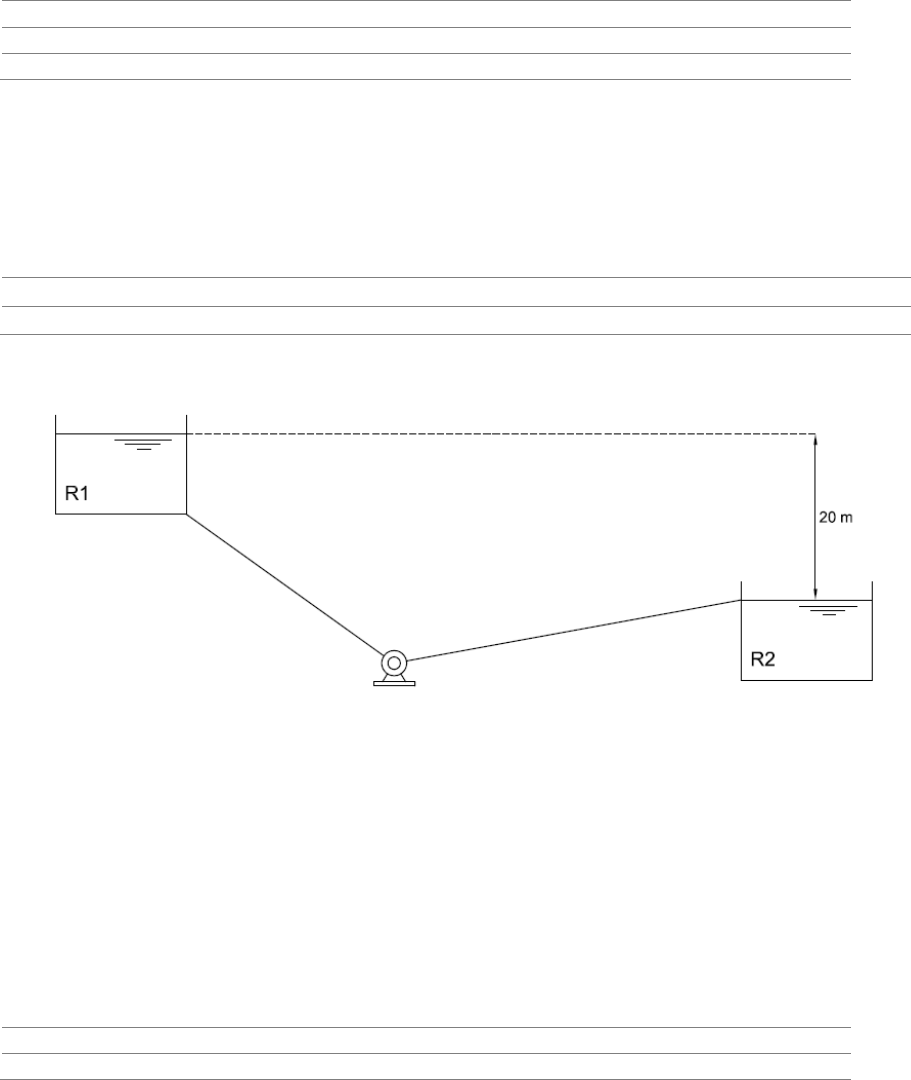
4) [6.4] A adutora mostrada na figura a seguir conduz 200 m3/h do reservatório R1 para o
R2. Objeti vando aumentar esta vazão, ser á introduzida uma bomba no ponto B, com as
características apresentadas no quadro.
Q (m3/h)
0,0
50,0
100,0
150,00
200,0
250,0
300,0
350,0
400,0
450,0
500,0
Hm (m)
80,0
79,0
77,0
73,8
70,0
65,0
59,0
52,0
43,0
35,0
25,0
a) Determinar a vazão transportada entre os reservatórios após a colocação da bomba.
b) Fazer um esquema mostrando a linha piezométrica entre dois reservatórios, após a
colocação da bomba.
5) [6.6] A curva característica de duas bombas iguais associadas em paralelo apresenta os
seguintes dados:
Q (l/s)
0,0
2,0
4,0
6,0
8,0
10,0
12,0
14,0
Hm (m)
15,5
15,2
14,6
13,4
12,0
10,0
7,6
4,4
Com um desníve l geométrico de 6,0 m, as duas bombas ligadas recalcam 10 l/s sob a
altura manométrica de 10,0 m. Qual a altura manométrica e qual a vazão de apenas um
bomba ligada?
6) [6.9] Uma bomba movida por um motor de 3500 rpm deve trabalhar num sistema cuja
altura máxima de sucção é 2,0 m. Verificar se esta bomba cavita ao trabalhar com uma
vazão de 10 l/s.
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
4
Considerar:
- diâmetro da sucção: 100 mm
- comprimento da tubulação de sucção: 7,0 m
- coeficiente de perda de carga da fór mula de Hazen-Willia ms: 130
- desprezar as perdas de carga localizadas .
7) [6.10] Uma elevatória está sendo projetada para recalcar 500 m3/h, a uma altura
geométrica de 30,0 m, através de uma adutora de 400 mm de diâmetro, 12 km de
comprimento e coeficiente de perda de carga da fórmula Universal igual a 0,022. A
perda de carga localizada prevista é de 10U 2/2g. Visando aproveitar uma bomba
existente, cujas características, à rotação de 1800 rpm, são mostradas no quadro a seguir,
pede-se:
a) ponto de trabalho;
b) determinar a rotação para que a bomba trabalhe exatamente com a vazão de projeto.
Q (m3/h)
0
100
200
300
400
500
600
Hm (m)
120
119
115
109
100
87
70
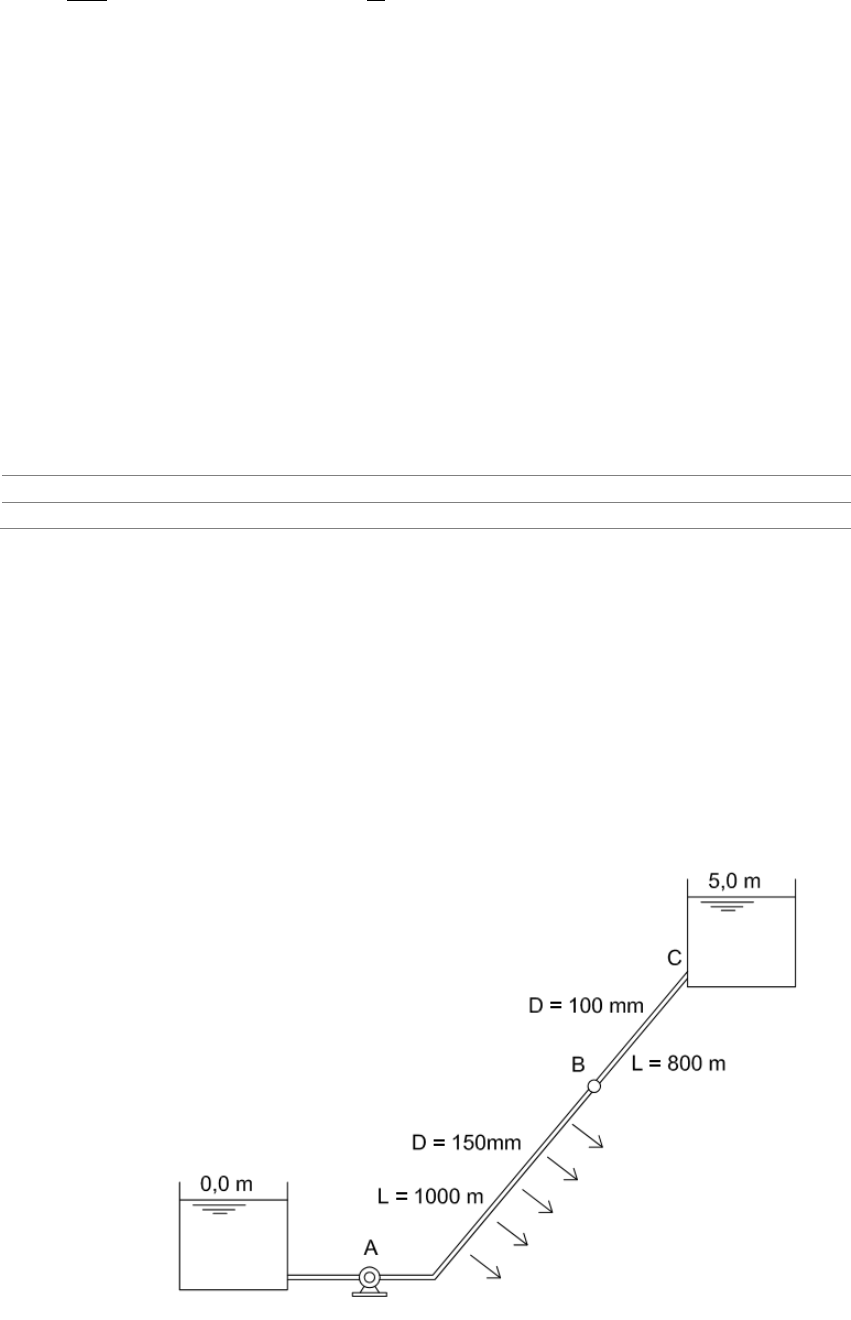
8) [5.2 - Hidráulica Básica] O esquema de bombeamento mostrado na figura abaixo é
constituído de tubulações de aço com coeficiente de rugosidade da fórmula de Hazen-
Williams C = 130. Da bomba até o ponto B, existe uma distribuição de vazão e m
marcha com taxa de distribuição constante e igual a q = 0,005 l/sm. Para a cur va
característica da bomba, dada na figura, determine a vazão que chega ao reservatório
superior e a cota piezométrica no ponto B. Despreze as perdas localizadas e a carga
cinética.
Sugestão: reveja o conceito de vazão fictícia e observe que os trechos AB e BC estã o
em “série”.
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
5
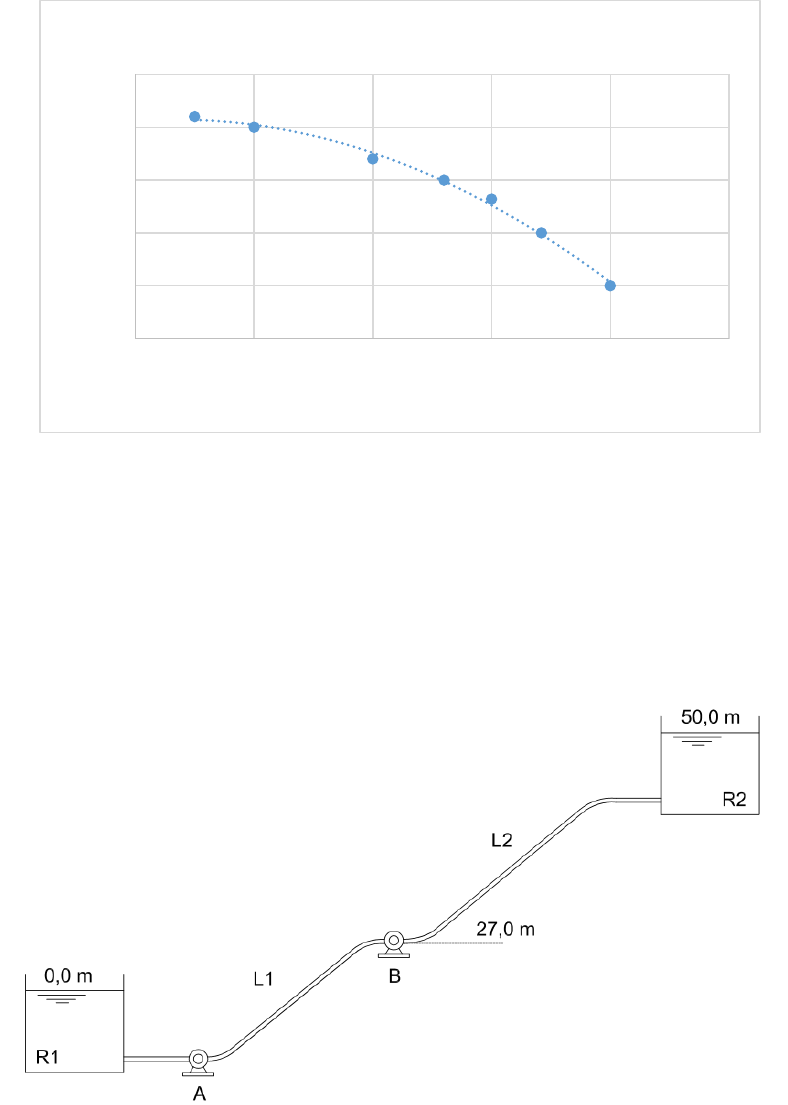
9) [5.3 Livr o de Exercícios – Hidráulica Básica] O sistema de bombeamento mostrado na
figura consiste de dois segmentos de tubos de mesmo diâmetro e igual a 750 mm, fator
de atrito F = 0,023 e comprimentos L1 = 5000 m e L2 = 7500 m. A bo mba A tem
potência de 10 3kW e a pressão na entrada da bomba B é 150 kPa. Determine a vazão
recalcada, as alturas manométricas das bombas e a potência da bomba B. Ambas as
bombas tem rendimento igual a 75%. Despreze a carga cinética e a perda na sucção da
bomba A.
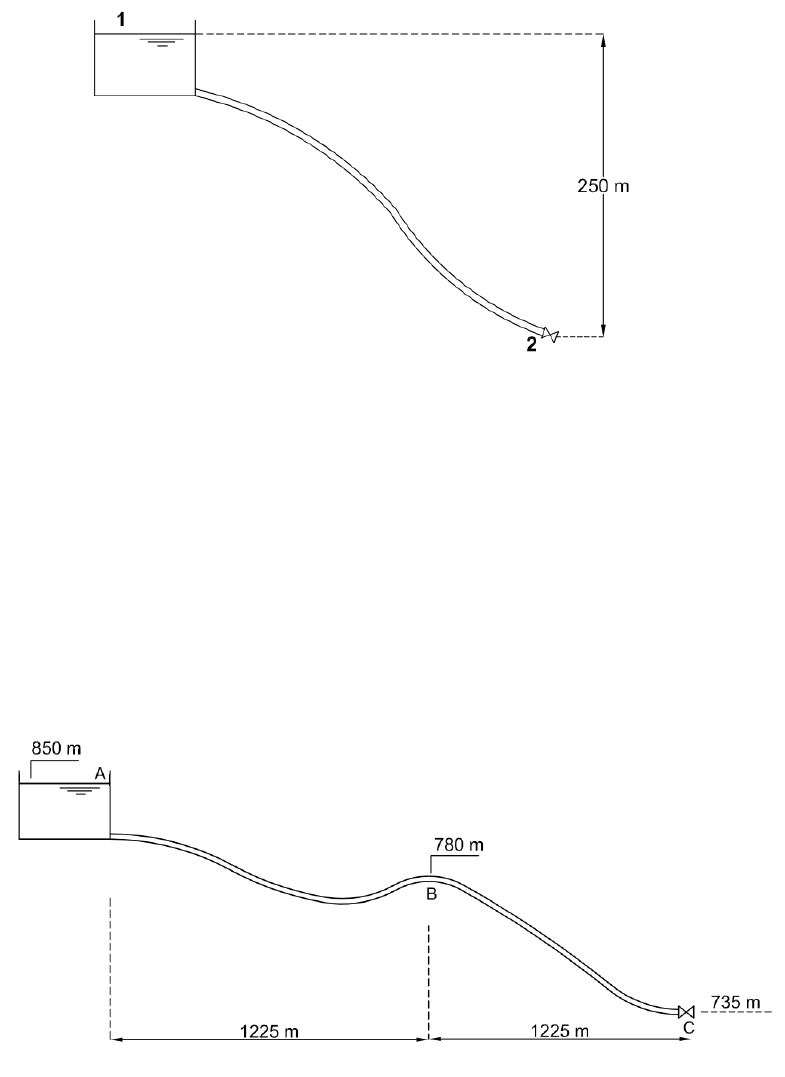
10) (Problema VI.1 ) Um conduto forçado de aço (C = 130) com 500 m de comprimento,
800 mm de diâmetro e 12 mm de espessura , está assentado conforme a figura abaixo. O
registro localizado no ponto mais baixo é manobrado em 8 s. Desconsiderando -se as
perdas de carga e sabendo-se que a velocidade média do fluido é de 3 m/s, pede-se, para
a seção junto ao registro:
a) Pressão em “2” com registro fechado;
b) Pressão em “2” com registro aberto;
c) Sobrepressão;
0
5
10
15
20
25
0 5 10 15 20 25
H (m)
Q (l/s)
Curva da bomba
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
6
d) Pressão máxima;
e) Pressão mínima.
11) (Problema VI. 2) Através de uma adutora que funciona por gravidade construída com
FoFo, comprimento igual a 2450 m e diâmetro 250 mm, escoa uma vazão de 70 l/s. Em sua
extremidade de jusante encontra-se instalado um registro de gaveta. Sabe-se que:
Tempo de fechamento do registro: 58 s;
Espessura do tubo: 10 mm;
Diâmetro: 250 mm;
Elevação do NA à montante da adutora: 850 m;
Elevação do ponto médio da adutora: 780 m;
Elevação do eixo do registro de gaveta: 735 m.
Desconsiderando-se todas as perdas de carga, verifique se o tubo sofrerá cola pso, sabendo-se
que a pressão máxima de serviço é de 3,5 Mpa (350 mca).
12) (Problema VI. 3) Uma tubulação de FoFo com L = 250 m, D = 700 mm e “e” = 6,25 mm
transporta água à velocidade U = 3,6 m/s. Junto à válvula montada na extr emidade de
jusante da tubulação a pressão estática é de 50 mca. Sabendo-se que a válvula fecha-se
completamente em 3,25 s e que o tubo res iste à 25 kgf/cm², verifique se há risco de
ruptura. Caso a tubulação seja segura, calcule o fator de segurança.
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
7
13) (Problema VI. 4) Seja a tubulação de aço com D = 700 mm e “e” = 6,35 mm, sendo L =
250 m, U = 3,6 m/s, t = 2,1 s, com pressão estática sobre a válvula igual a 50 m. Calcule
a sobrepressão para os diversos modelos.
14) (Problema VI. 5) Um sistema de recalque foi dimensionado para vazão de 260 L/s e sua
tubulação de recalque é de aço, com 600,5 m de co mprimento, diâmetro 550 mm e
paredes de 14 mm de espessura. A Altura manométrica é de 35 m. O conjunto funciona
com a rotação de 1770 rpm e a eficiência de 80%. Na saí da da bomba existe uma
válvula de retenção que impede a sua rotação em sentido inverso. Calcule:
a) A pressão máxima no início do conduto de recalque, quando int errompe a energia elétrica
(desconsidere as perdas localizadas e C=100).
b) O fator de segurança do material caso seja 27 kgf/cm² sua tensão de ruptura.
15) (Márcio Baptista) [7.1] A galeria da avenida Álvaro da Silveira, situada na região da
Pampulha, em Belo Horizonte, foi implantada em concreto moldado in loco, de forma
retangular com largura de base de 4,50 m. Sabendo -se que ela deverá funcionar com
uma profundidade de fluxo de 1,60 m e que a velocidade média de escoamento prevista
é de 3,20 m/s, pede-se calcular a vazão transportada.
16) (Márcio Baptista) [7.2] Calcular os parâmetros hidráulicos característicos de um canal
trapezoidal de largura de base de 3,00 m, taludes laterais com Z = 1,5 e profundidade
2,60 m. Calcular também a velocidade média de escoamento, supondo que ele transporta
uma vazão de 60 m3/s nas condições de projeto.
17) (Márcio Baptista) [7.3] A adutor a do Sistema Rio da s Velhas, implantada para
abastecimento de água da cidade de Belo Horizonte, possui um trecho em canal, com
seção circular em concreto liso , com diâmetro interno de 2,40 m, asse ntado com
declividade de 1%. Determinar a veloc idade de escoamento para a condição de
funcionamento correspondente à meia seção e vazão de 6 m3/s.
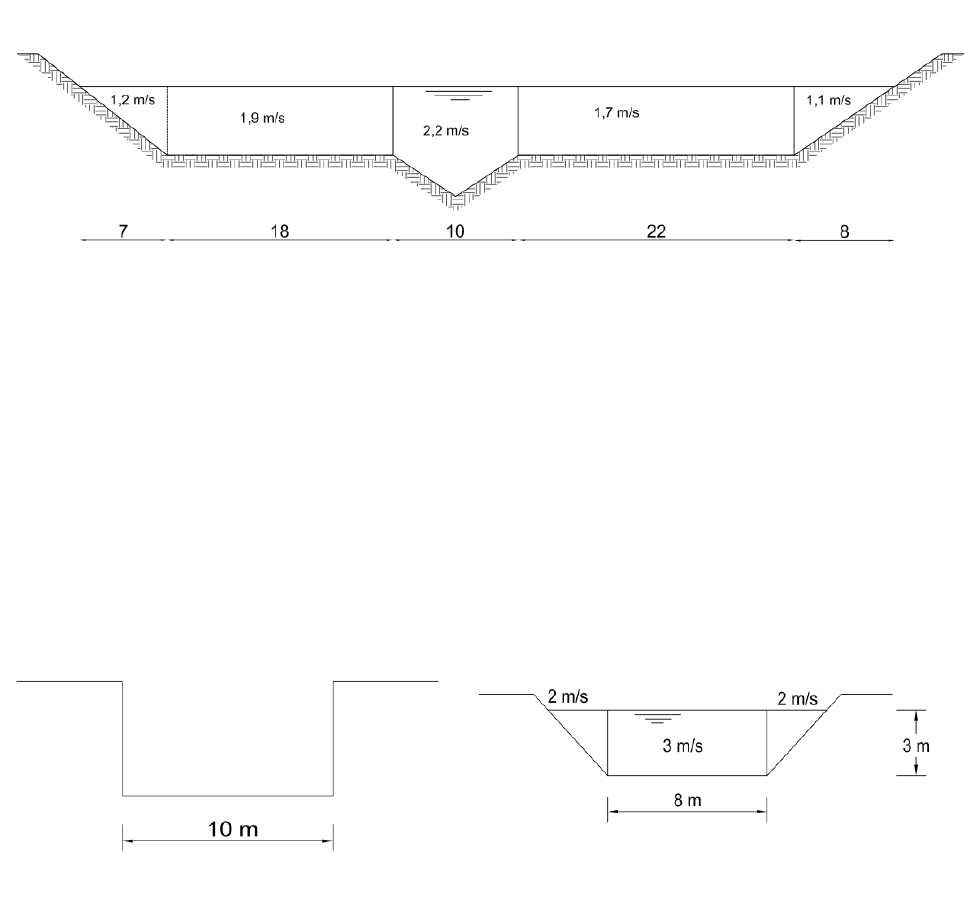
18) (Márcio Baptista) [7.4] Foram efetuadas medições de velocidades em um curso d’água,
como indicado na figura. Pede-se calcular os parâmetros hidráulicos característicos da
seção, a vazão e a velocidade média.
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
8
19) (Márcio Baptista) [7.8] Um canal de irrigação, inicialmente com seção retangular (seção
1) e posteriormente trapezoidal, com taludes inclinados de 45° (seção 2), conforme
indicado nas figuras, é implantado com as cotas de fundo de 818,00 m e 812,50 m,
respectivamente. Pede-se:
a) Calcular a vazão transportada, supondo escoamento permanente com a profundidade
de 3,00 m na seção 2;
b) Definir o de Coeficiente de Coriolis para as seções 1 e 2, conhecendo - se as
velocidades médias nas sub-áreas indicadas na seção 2 e supondo-se que a velocidade
média de 2,75 m/s é constante em toda a seção 1;
c) Determinar a pressão no fundo do canal da seção 1 e calcular a perda de carga total
entre as seções 1 e 2.
20) (Márcio Baptista) [8.1] Um canal triangular com Z = 1,00 transporta 0,80 m3/s com
uma profundidade de 1,20 m. Determinar o regime de escoamento.
21) (Márcio Baptista) [8.2] Um canal retangul ar com lar gura de 8 m transporta uma vazão
de 40 m3/s. Determinar a profundidade e a velocidade crítica.
22) (Márcio Baptista) [8.3] Calcular a vazão e velocidade críticas para um canal trapezoidal
com largura da base de 4,00 m e taludes 4(H):1(V), supondo que a profundidade crítica
é de 2,00 m.
23) (Márcio Baptista) [8.4] Calcul ar a vazão em um canal ret angular largo, sabendo que a
profundidade crítica é de 2,20 m.
24) (Márcio Baptista) [8.5] Traçar a curva de energia específica para um canal, de seção
retangular com 10 m de largura, transportando 25 m3/s.
25) (Márcio Baptista) [8.7] Um canal retangular com largura de 50 m transporta uma vazão
de 200 m3/s com uma profundidade de escoamento inicial de 2 m. Após uma mudança
de declividade, a profundidade passa a ser 0,60 m. Supondo ausência de perda de carga,
pede-se:
a) Construir a curva de energia específica;
b) Determinar a energia crítica;
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
9
c) Determinar a energia específica no segundo trecho.
26) (Márcio Baptista) [8.9] Em u m canal retangular com 1,80 m de largura ocor re escoamento
com profundidade de 0,80 m e velocidade de 1,00 m/s. Determ inar qual a profundidade de
escoamento em uma seção do canal onde se observa um estrei tamento gradual para 1,50 m de
largura, supondo ausência de perda de carga.
27) (Problema VII. 6) Um canal retangular com 8 m de largura transporta uma vazão de 96
m³/s com profundidade de 4 m. Por razões estruturais este canal sofre uma redução de largura
para 6 m em uma extensão de 5 m. Considerando uma transição sem perda de carga, esboçar o
perfil da linha d’água a montante e a jusante.
28) (Problema VII. 7) Um canal retangul ar com 50 m de lar gura transporta uma vazão de 250
m³/s com profundidade de 5 m. Com vistas forçar a ocorrência do regime crítico no canal
através da implantação de uma singularidade, determinar:
a) A altura de uma soleira implantada no fundo do canal, sendo que a largura deve
permanecer constante;
b) Um estreitamento de seção do canal, sendo que o nível do fundo deve permanecer
inalterado.
Considerar que não há perda de carga.
29) (Márcio Baptista) [8.13] Em uma canal eta de drenagem, com 0,40 m de l argura, foi
implantada uma soleir a forçando a ocorrência do regime crítico, com profundidade de 0,08 m.
Sabendo-se que as profundidades a montante e a jusante da soleira são, respectivamente, 0,25
m, e 0,05 m, determinar os regimes de escoamento nestes pon tos e calcular a vazão em
trânsito.
30) (Problema VII. 8) Considere um canal trapezoidal revestido com grama, com
inclinação dos taludes 1(V):2(H), base de 7 m d eclividade 0,06% e coeficiente de manning n
= 0,025. Determinar a vazão transportada sabendo-se que a profundidade é de 5 m.
31) (Problema VII. 9) Um canal trapezoidal com largura de base igual a 3 m e tal udes laterais
de 1:1 transporta 15 m³/s. Calcule a profundidade do escoamento sabendo -se que n = 0,0135 e
I = 0,005 m/m.
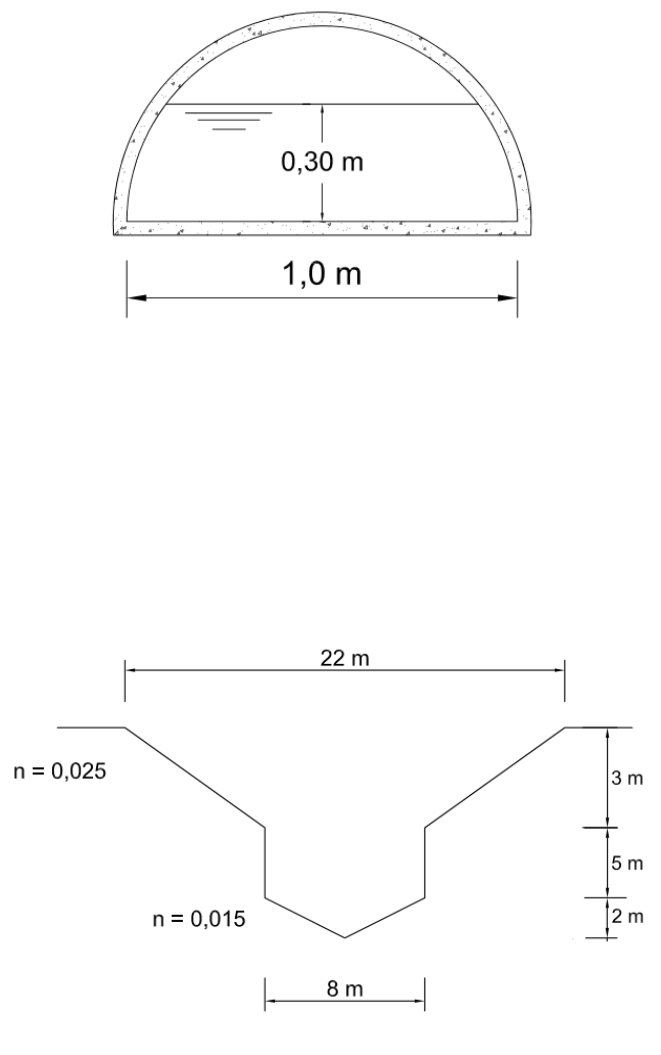
32) (Márcio Baptista) [8.22] [Hidrálica Básica – modificada] Na figura abaixo está ilustrada
uma galeria semicircular de diâmetro igual a 1,0 m, com declividade de fundo igual a 0,3% e
cuja lâmina d’água é de y0 = 0,30 m.
a) Determinar a capacidade de vazão da galeria (n = 0,014).
b) A inclinação cuja energia específica é mínima é maior, menor ou igual a 0,3%?
Justifique.
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental
10
33) (Márcio Baptista) [9.3] Qual é a declividade de um canal trapezoidal gramado, com base
de 10 m e taludes 3(H):1(V), transportando 10 m3/s com uma profundidade de 0,75 m.
34) (Márcio Baptista) [9.5] Dado o canal de drenagem da figura, com seção composta em
concreto e revestimento vegetal, implantado com declividade longitudinal de 0,08%, pede-se:
a) Calcular sua capacidade máxima de vazão em escoamento uniforme;
b) Definir quais seriam as alternativas possíveis para aumentar -se a capacidade de vazão do
canal, mantendo-se a mesma largura superficial e a mesma profundidade de escavação.
35) (Má rcio Baptista) [8.12] [Livro de exercícios – Hidráulica Básica ] Determinar a
capacidade de vazão de um canal trapezoidal, conforme a figura abaixo. Os taludes e fundo
são rev estidos com alvenaria de pedra seca em b oas condições (n = 0,033) e a declividade de
fundo é igual a I = 0,0005 m/m. Determinar o comprimento adicional L, na lar gura de fundo,
que é necessário para que a capacidade de vazão seja 43% superior a calculada, sem alt erar a
profundidade do escoamento do canal. A inclinação dos taludes, a declividade de fundo e o
material de revestimento das paredes e fundo permanecem iguais a situação original.
Prévia do material em texto
Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 1 Hidráulica Geral Segunda Lista de Exercícios Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 2 1) [6.1] Uma bomba centrífuga, com as características Hm x Q mostradas no quadro a seguir, produziu 50 l/s, quando foi instalada numa adutora que interliga dois reservatórios cuja diferença entre os níveis de água é 30,0 m. Após 20 anos de funcionamento deste sistema, verificou-se que a vazão havia sido reduzida para 40 l/s devido ao aumento da perda de carga na tubulação. Desprezando as perdas de carga localizadas, pede-se determinar, após 20 anos de uso, a perda de carga contínua na tubulação e o aumento percentual do coeficiente de perda de carga da fórmula Universal. Q (l/s) 0,0 10,0 20,0 30,0 40,0 50,0 60,0 70,0 80,0 Hm (m) 80,0 75,1 69,6 63,6 57,1 50,0 42,4 34,3 25,6 2) [6.2] Uma bomba centrífuga foi testada em laboratório numa instalação cujo esquema de medição de pressão é mostrado na figura abaixo. As informações obtidas nos testes estão no quadro a seguir. Pede-se determinar a curva característica Hm x Q da bomba. Teste Vazão (l/s) Manômetro de mercúrio h1 (mm) Manômetro metálico P2 (k Pa) 1 40,0 120 490 2 70,0 160 372 3 100,0 190 245 3) [6.3] Uma bomba testada em laboratório apresentou as características mostradas no quadro a seguir. Esta bomba deverá ser utilizada numa estação elevatória cuja altura geométrica é 25 m, ligada a uma adutora com coeficiente de perda de carga da fórmula Universal igual a 0,025 e extensão de 3556 m. As peças, conexões e aparelhos provocam uma perda de carga localizada de 10 U2/2g. Pede-se selecionar o diâmetro da tubulação para permitir o escoamento de 80 l/s e calcular a potência consumida. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 3 Vazão (l/s) 0 20 40 60 80 100 120 Altura manométrica (m) 60 59 57 52 45 35 22 Eficiência (%) - 42 58 71 75 69 54 4) [6.4] A adutora mostrada na figura a seguir conduz 200 m3/h do reservatório R1 para o R2. Objetivando aumentar esta vazão, será introduzida uma bomba no ponto B, com as características apresentadas no quadro. Q (m3/h) 0,0 50,0 100,0 150,00 200,0 250,0 300,0 350,0 400,0 450,0 500,0 Hm (m) 80,0 79,0 77,0 73,8 70,0 65,0 59,0 52,0 43,0 35,0 25,0 a) Determinar a vazão transportada entre os reservatórios após a colocação da bomba. b) Fazer um esquema mostrando a linha piezométrica entre dois reservatórios, após a colocação da bomba. 5) [6.6] A curva característica de duas bombas iguais associadas em paralelo apresenta os seguintes dados: Q (l/s) 0,0 2,0 4,0 6,0 8,0 10,0 12,0 14,0 Hm (m) 15,5 15,2 14,6 13,4 12,0 10,0 7,6 4,4 Com um desnível geométrico de 6,0 m, as duas bombas ligadas recalcam 10 l/s sob a altura manométrica de 10,0 m. Qual a altura manométrica e qual a vazão de apenas um bomba ligada? 6) [6.9] Uma bomba movida por um motor de 3500 rpm deve trabalhar num sistema cuja altura máxima de sucção é 2,0 m. Verificar se esta bomba cavita ao trabalhar com uma vazão de 10 l/s. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 4 Considerar: 𝑃𝑎𝑡𝑚 𝑎𝑏𝑠 𝛾 = 9,8 𝑚𝑐𝑎 Pv 𝛾 = 0,2 mca - diâmetro da sucção: 100 mm - comprimento da tubulação de sucção: 7,0 m - coeficiente de perda de carga da fórmula de Hazen-Williams: 130 - desprezar as perdas de carga localizadas. 7) [6.10] Uma elevatória está sendo projetada para recalcar 500 m3/h, a uma altura geométrica de 30,0 m, através de uma adutora de 400 mm de diâmetro, 12 km de comprimento e coeficiente de perda de carga da fórmula Universal igual a 0,022. A perda de carga localizada prevista é de 10U2/2g. Visando aproveitar uma bomba existente, cujas características, à rotação de 1800 rpm, são mostradas no quadro a seguir, pede-se: a) ponto de trabalho; b) determinar a rotação para que a bomba trabalhe exatamente com a vazão de projeto. Q (m3/h) 0 100 200 300 400 500 600 Hm (m) 120 119 115 109 100 87 70 8) [5.2 - Hidráulica Básica] O esquema de bombeamento mostrado na figura abaixo é constituído de tubulações de aço com coeficiente de rugosidade da fórmula de Hazen- Williams C = 130. Da bomba até o ponto B, existe uma distribuição de vazão em marcha com taxa de distribuição constante e igual a q = 0,005 l/sm. Para a curva característica da bomba, dada na figura, determine a vazão que chega ao reservatório superior e a cota piezométrica no ponto B. Despreze as perdas localizadas e a carga cinética. Sugestão: reveja o conceito de vazão fictícia e observe que os trechos AB e BC estão em “série”. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 5 9) [5.3 Livro de Exercícios – Hidráulica Básica] O sistema de bombeamento mostrado na figura consiste de dois segmentos de tubos de mesmo diâmetro e igual a 750 mm, fator de atrito F = 0,023 e comprimentos L1 = 5000 m e L2 = 7500 m. A bomba A tem potência de 103kW e a pressão na entrada da bomba B é 150 kPa. Determine a vazão recalcada, as alturas manométricas das bombas e a potência da bomba B. Ambas as bombas tem rendimento igual a 75%. Despreze a carga cinética e a perda na sucção da bomba A. 10) (Problema VI.1 ) Um conduto forçado de aço (C = 130) com 500 m de comprimento, 800 mm de diâmetro e 12 mm de espessura, está assentado conforme a figura abaixo. O registro localizado no ponto mais baixo é manobrado em 8 s. Desconsiderando-se as perdas de carga e sabendo-se que a velocidade média do fluido é de 3 m/s, pede-se, para a seção junto ao registro: a) Pressão em “2” com registro fechado; b) Pressão em “2” com registro aberto; c) Sobrepressão; 0 5 10 15 20 25 0 5 10 15 20 25 H ( m ) Q (l/s) Curva da bomba Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 6 d) Pressão máxima; e) Pressão mínima. 11) (Problema VI. 2) Através de uma adutora que funciona por gravidade construída com FoFo, comprimento igual a 2450 m e diâmetro 250 mm, escoa uma vazão de 70 l/s. Em sua extremidade de jusante encontra-se instalado um registro de gaveta. Sabe-se que: Tempo de fechamento do registro: 58 s; Espessura do tubo: 10 mm; Diâmetro: 250 mm; Elevação do NA à montante da adutora: 850 m; Elevação do ponto médio da adutora: 780 m; Elevação do eixo do registro de gaveta: 735 m. Desconsiderando-se todas as perdas de carga, verifique se o tubo sofrerá colapso, sabendo-se que a pressão máxima de serviço é de 3,5 Mpa (350 mca). 12) (Problema VI. 3)Uma tubulação de FoFo com L = 250 m, D = 700 mm e “e” = 6,25 mm transporta água à velocidade U = 3,6 m/s. Junto à válvula montada na extremidade de jusante da tubulação a pressão estática é de 50 mca. Sabendo-se que a válvula fecha-se completamente em 3,25 s e que o tubo resiste à 25 kgf/cm², verifique se há risco deruptura. Caso a tubulação seja segura, calcule o fator de segurança. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 7 13) (Problema VI. 4) Seja a tubulação de aço com D = 700 mm e “e” = 6,35 mm, sendo L = 250 m, U = 3,6 m/s, t = 2,1 s, com pressão estática sobre a válvula igual a 50 m. Calcule a sobrepressão para os diversos modelos. 14) (Problema VI. 5) Um sistema de recalque foi dimensionado para vazão de 260 L/s e sua tubulação de recalque é de aço, com 600,5 m de comprimento, diâmetro 550 mm e paredes de 14 mm de espessura. A Altura manométrica é de 35 m. O conjunto funciona com a rotação de 1770 rpm e a eficiência de 80%. Na saída da bomba existe uma válvula de retenção que impede a sua rotação em sentido inverso. Calcule: a) A pressão máxima no início do conduto de recalque, quando interrompe a energia elétrica (desconsidere as perdas localizadas e C=100). b) O fator de segurança do material caso seja 27 kgf/cm² sua tensão de ruptura. 15) (Márcio Baptista) [7.1] A galeria da avenida Álvaro da Silveira, situada na região da Pampulha, em Belo Horizonte, foi implantada em concreto moldado in loco, de forma retangular com largura de base de 4,50 m. Sabendo-se que ela deverá funcionar com uma profundidade de fluxo de 1,60 m e que a velocidade média de escoamento prevista é de 3,20 m/s, pede-se calcular a vazão transportada. 16) (Márcio Baptista) [7.2] Calcular os parâmetros hidráulicos característicos de um canal trapezoidal de largura de base de 3,00 m, taludes laterais com Z = 1,5 e profundidade 2,60 m. Calcular também a velocidade média de escoamento, supondo que ele transporta uma vazão de 60 m3/s nas condições de projeto. 17) (Márcio Baptista) [7.3] A adutora do Sistema Rio das Velhas, implantada para abastecimento de água da cidade de Belo Horizonte, possui um trecho em canal, com seção circular em concreto liso, com diâmetro interno de 2,40 m, assentado com declividade de 1%. Determinar a velocidade de escoamento para a condição de funcionamento correspondente à meia seção e vazão de 6 m3/s. 18) (Márcio Baptista) [7.4] Foram efetuadas medições de velocidades em um curso d’água, como indicado na figura. Pede-se calcular os parâmetros hidráulicos característicos da seção, a vazão e a velocidade média. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 8 19) (Márcio Baptista) [7.8] Um canal de irrigação, inicialmente com seção retangular (seção 1) e posteriormente trapezoidal, com taludes inclinados de 45° (seção 2), conforme indicado nas figuras, é implantado com as cotas de fundo de 818,00 m e 812,50 m, respectivamente. Pede-se: a) Calcular a vazão transportada, supondo escoamento permanente com a profundidade de 3,00 m na seção 2; b) Definir o de Coeficiente de Coriolis para as seções 1 e 2, conhecendo-se as velocidades médias nas sub-áreas indicadas na seção 2 e supondo-se que a velocidade média de 2,75 m/s é constante em toda a seção 1; c) Determinar a pressão no fundo do canal da seção 1 e calcular a perda de carga total entre as seções 1 e 2. 20) (Márcio Baptista) [8.1] Um canal triangular com Z = 1,00 transporta 0,80 m3/s com uma profundidade de 1,20 m. Determinar o regime de escoamento. 21) (Márcio Baptista) [8.2] Um canal retangular com largura de 8 m transporta uma vazão de 40 m3/s. Determinar a profundidade e a velocidade crítica. 22) (Márcio Baptista) [8.3] Calcular a vazão e velocidade críticas para um canal trapezoidal com largura da base de 4,00 m e taludes 4(H):1(V), supondo que a profundidade crítica é de 2,00 m. 23) (Márcio Baptista) [8.4] Calcular a vazão em um canal retangular largo, sabendo que a profundidade crítica é de 2,20 m. 24) (Márcio Baptista) [8.5] Traçar a curva de energia específica para um canal, de seção retangular com 10 m de largura, transportando 25 m3/s. 25) (Márcio Baptista) [8.7] Um canal retangular com largura de 50 m transporta uma vazão de 200 m3/s com uma profundidade de escoamento inicial de 2 m. Após uma mudança de declividade, a profundidade passa a ser 0,60 m. Supondo ausência de perda de carga, pede-se: a) Construir a curva de energia específica; b) Determinar a energia crítica; Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 9 c) Determinar a energia específica no segundo trecho. 26) (Márcio Baptista) [8.9] Em um canal retangular com 1,80 m de largura ocorre escoamento com profundidade de 0,80 m e velocidade de 1,00 m/s. Determinar qual a profundidade de escoamento em uma seção do canal onde se observa um estreitamento gradual para 1,50 m de largura, supondo ausência de perda de carga. 27) (Problema VII. 6) Um canal retangular com 8 m de largura transporta uma vazão de 96 m³/s com profundidade de 4 m. Por razões estruturais este canal sofre uma redução de largura para 6 m em uma extensão de 5 m. Considerando uma transição sem perda de carga, esboçar o perfil da linha d’água a montante e a jusante. 28) (Problema VII. 7) Um canal retangular com 50 m de largura transporta uma vazão de 250 m³/s com profundidade de 5 m. Com vistas forçar a ocorrência do regime crítico no canal através da implantação de uma singularidade, determinar: a) A altura de uma soleira implantada no fundo do canal, sendo que a largura deve permanecer constante; b) Um estreitamento de seção do canal, sendo que o nível do fundo deve permanecer inalterado. Considerar que não há perda de carga. 29) (Márcio Baptista) [8.13] Em uma canaleta de drenagem, com 0,40 m de largura, foi implantada uma soleira forçando a ocorrência do regime crítico, com profundidade de 0,08 m. Sabendo-se que as profundidades a montante e a jusante da soleira são, respectivamente, 0,25 m, e 0,05 m, determinar os regimes de escoamento nestes pontos e calcular a vazão em trânsito. 30) (Problema VII. 8) Considere um canal trapezoidal revestido com grama, com inclinação dos taludes 1(V):2(H), base de 7 m declividade 0,06% e coeficiente de manning n = 0,025. Determinar a vazão transportada sabendo-se que a profundidade é de 5 m. 31) (Problema VII. 9) Um canal trapezoidal com largura de base igual a 3 m e taludes laterais de 1:1 transporta 15 m³/s. Calcule a profundidade do escoamento sabendo-se que n = 0,0135 e I = 0,005 m/m. 32) (Márcio Baptista) [8.22] [Hidrálica Básica – modificada] Na figura abaixo está ilustrada uma galeria semicircular de diâmetro igual a 1,0 m, com declividade de fundo igual a 0,3% e cuja lâmina d’água é de y0 = 0,30 m. a) Determinar a capacidade de vazão da galeria (n = 0,014). b) A inclinação cuja energia específica é mínima é maior, menor ou igual a 0,3%? Justifique. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 10 33) (Márcio Baptista) [9.3] Qual é a declividade de um canal trapezoidal gramado, com base de 10 m e taludes 3(H):1(V), transportando 10 m3/s com uma profundidade de 0,75 m. 34) (Márcio Baptista) [9.5] Dado o canal de drenagem da figura, com seção composta em concreto e revestimento vegetal, implantado com declividade longitudinal de 0,08%, pede-se: a) Calcular sua capacidade máxima de vazão em escoamento uniforme; b) Definir quais seriam as alternativas possíveis para aumentar-se a capacidade de vazão do canal, mantendo-se a mesma largura superficial e a mesma profundidade de escavação. 35) (Márcio Baptista) [8.12] [Livro de exercícios – Hidráulica Básica]Determinar a capacidade de vazão de um canal trapezoidal, conforme a figura abaixo. Os taludes e fundo são revestidos com alvenaria de pedra seca em boas condições (n = 0,033) e a declividade de fundo é igual a I = 0,0005 m/m. Determinar o comprimento adicional L, na largura de fundo, que é necessário para que a capacidade de vazão seja 43% superior a calculada, sem alterar a profundidade do escoamento do canal. A inclinação dos taludes, a declividade de fundo e o material de revestimento das paredes e fundo permanecem iguais a situação original. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 11 36) (Problema VII. 10) Determinar o diâmetro “D” de uma galeria construída com tubos pré- moldados de concreto para transportar 1200 l/s implantado com declividade I = 1,5% sendo que o tirante d’água está limitado à 80% do diâmetro. Considere Umáx = 4,5 m/s. 37) (Problema VII. 11) Dimensione um canal retangular em concreto (n=0,015) com declividade I = 0,0018 m/m para funcionar na condição de máxima eficiência hidráulica conduzindo 50 m³/s. 38) (Rodrigo de Melo Porto – 7.5) O canal cuja seção é mostrada na figura transporta uma vazão Q = 4,0 m³/s. Classifique o escoamento. Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 12 39) (Rodrigo de Melo Porto – 8.10) Determinar a capacidade de vazão do canalete de drenagem de pé de talude, em uma rodovia, revestido de concreto em condições regulares, com declividade de fundo I = 0,005 m/m, em condições de regime permanente e uniforme, conforme figura. O escoamento é fluvial ou torrencial? Respostas 1: ∆ℎ = 27,1 𝑚, aumento de 112%. 2: 𝐻𝑚 = − 𝑄2 1714,29 − 𝑄 3,15 + 65,94. 3: 𝐷 = 300 𝑚𝑚; 𝑃𝐵 = 64,0 𝑐𝑣. 4: 𝑄 = 370 𝑚3 ℎ.⁄ 5: 𝐻𝑚 = 7,44 𝑚; 𝑄1𝐵 = 6𝑙/𝑠. 6: 7,46 𝑚; 𝑁𝑃𝑆𝐻𝑅 = 2,96 𝑚. Não cavita. 7: : a) 𝐻𝑚 = 80,0 𝑚; 𝑄 = 547 𝑚 3 ℎ⁄ . b) 𝑛 = 1645 𝑟𝑝𝑚 8: 𝑄 = 7 𝑙 𝑠⁄ ; 𝐶𝑃𝐵 = 13,0 𝑚. 9: 𝑄 = 0,963 𝑚3 𝑠⁄ ; 𝐻𝐴 = 79,47; 𝐻𝐵 = 63,44 𝑚; 𝑃𝐵 = 797,45 𝑘𝑊. 10: a) 𝑃2 𝛾⁄ = 250 𝑚𝑐𝑎; b) 𝑃2 𝛾⁄ = 249,6 𝑚𝑐𝑎; c) ℎ𝑎 = 38,2 𝑚𝑐𝑎; d) 𝑃𝑀Á𝑋 𝛾 = 287,8 𝑚𝑐𝑎⁄ ; e) 𝑃𝑀Í𝑁 𝛾 = 211,4 𝑚𝑐𝑎⁄ . 11: 𝑃𝑀Á𝑋 𝛾⁄ = 127,32 𝑚𝑐𝑎. O tubo não sofrerá colapso. 12: A tubulação é segura e o fator de segurança é 2,3 13: 1º modelo: 86,76 mca; 2º modelo (Spane): 77,58 mca; 3º modelo (Johnson): 66,76 mca 14: a) 56,25 mca b) FS = 4,8 15: 𝑄 = 23,04 𝑚3/𝑠. 16: 𝐴 = 17,94 𝑚2, 𝐵 = 10,80 𝑚, 𝑃 = 12,37 𝑚, 𝑅ℎ = 1,45 𝑚, 𝑦ℎ = 1,66 𝑚, 𝑈 = 3,34 𝑚/𝑠. 17: 𝑈 = 2,65 𝑚/𝑠. 18: 𝐴 = 227,00 𝑚2; 𝐵 = 80,00 𝑚; 𝑃 = 81,81 𝑚; 𝑅ℎ = 2,77 𝑚; 𝑦ℎ = 2,84 𝑚; 𝑦 = 5 𝑚; 𝑄 = 407,75 𝑚3 𝑠⁄ ; 𝑈 = 1,80 𝑚 𝑠⁄ . Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 13 19: a) 𝑄 = 90,00 𝑚3 𝑠⁄ ; b) 𝛼1 = 1,00; 𝛼2 = 1,07; c) 𝑦 = 3,27 𝑚; ∆ℎ = 5,75 𝑚. 20: 𝐹𝑟 = 0,23. Regime Fluvial. 21: 𝑦𝐶 = 1,37 𝑚; 𝑈 = 3,65 𝑚/𝑠. 22: 𝑄 = 82,34 𝑚3 𝑠⁄ ; 𝑈 = 3,43 𝑚/𝑠. 23: 𝑞 = 10,22 𝑚3 𝑠. 𝑚⁄ . 24: Curva da energia específica 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 y( m ) E(m) Energia específica Professor Celso Bandeira Departamento de engenharia sanitária e ambiental 14 25: a) Curva da energia específica b) 𝐸𝐶 = 1,77 𝑚; c) 𝐸 = 2,88 𝑚. 26: 𝑦 = 0,77 𝑚. 27: 28: a) z = 3 m; b) 12,9 m 29:𝑄 = 0,028 𝑚3 𝑠⁄ ; 𝐹𝑟0,25 = 0,18 (𝑟𝑒𝑔𝑖𝑚𝑒 𝑓𝑙𝑢𝑣𝑖𝑎𝑙); 𝐹𝑟0,05 = 2,00 (𝑟𝑒𝑔𝑖𝑚𝑒 𝑡𝑜𝑟𝑟𝑒𝑛𝑐𝑖𝑎𝑙) 30: 𝑄 = 0,028 𝑚3 𝑠⁄ 31: y = 0,954 m 32: a) 𝑄 = 0,339 𝑚3 𝑠⁄ ; b) É maior que 0,3%. 33: Adotando n = 0,035, 𝐼 = 0,27%. 34: a) 𝑄 = 302 𝑚3 𝑠⁄ b) Diminuir a rugosidade do canal, alterar a geometria do canal. 35: 𝑄 = 1,48 𝑚3 𝑠⁄ ; 𝐿 = 1 𝑚. 36: D = 800 mm 37: y = 2,7 m B = 5,4 m 38: Escoamento turbulento 39: Q = 0,050 m³/s 0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 7 8 9 10 y( m ) E(m) Energia Específica Pow ered by TCPDF (www.tcpdf.org) Pow ered by TCPDF (www.tcpdf.org) Pow ered by TCPDF (www.tcpdf.org) Pow ered by TCPDF (www.tcpdf.org) Pow ered by TCPDF (www.tcpdf.org) 2 ÍNDICE CAPÍTULO 1 ........................................................................................................... 3 Página 19 exemplo 1.1 .............................................................................................. 4 Página 22 exemplo 1.3 .............................................................................................. 5 Pág. 25 numero 1.11 ................................................................................................. 6 Pág. 25 numero 1.12 ................................................................................................. 7 Pág. 26 numero 1.13 ................................................................................................. 8 Pág. 26 numero 1.14 ................................................................................................. 9 CAPÍTULO 2 ......................................................................................................... 10 Pág. 59 exemplo 2.8 ............................................................................................... 11 Pág. 63 numero 2.14 ............................................................................................... 12 Pág. 67 numero 2.33 ............................................................................................... 13 Pág. 67 numero 2.34 ............................................................................................... 14 Pág. 68 numero 2.35 ............................................................................................... 15 Pág. 68 numero 2.36 ............................................................................................... 16 CAPÍTULO 3 ......................................................................................................... 17 Página 85 exemplo 3.3 ............................................................................................ 18 Página 87 exemplo 3.4 ............................................................................................ 19 Pág. 88 numero 3.1 ................................................................................................. 20 Pág. 89 numero 3.4 ................................................................................................. 21 Pág. 91 numero 3.8 ................................................................................................. 23 Pág. 91 numero 3.8 (continuação) .......................................................................... 24 Pág. 92 numero 3.11 ...............................................................................................25 Pág. 92 numero 3.13 ............................................................................................... 26 CAPÍTULO 4 ......................................................................................................... 27 Pág. 105 exemplo 4.2 ............................................................................................. 29 Pág. 109 exemplo 4.3 ............................................................................................. 30 Pág. 118 numero 4.2 ............................................................................................... 31 Pág. 118 numero 4.4 ............................................................................................... 33 Pág. 118 numero 4.5 ............................................................................................... 34 Pág. 119 numero 4.6 ............................................................................................... 35 Pág. 119 numero 4.6 (continuação) ........................................................................ 36 Pág. 119 numero 4.7 ............................................................................................... 37 Pág. 120 numero 4.8 ............................................................................................... 38 Pág. 120 numero 4.9 ............................................................................................... 39 Pág. 120 numero 4.10 ............................................................................................. 40 Pág. 121 numero 4.11 ............................................................................................. 41 Pág. 121 numero 4.12 ............................................................................................. 42 Pág. 121 numero 4.13 ............................................................................................. 43 Pág. 121 numero 4.14 ............................................................................................. 44 Pág. 121 numero 4.15 ............................................................................................. 45 Pág. 122 numero 4.16 ............................................................................................. 46 Pág. 122 numero 4.17 ............................................................................................. 47 CAPÍTULO 5 ......................................................................................................... 48 Pág. 161 numero 5.2 .................................................Erro! Indicador não definido. CAPÍTULO 1 CAPÍTULO 1 4 Página 19 exemplo 1.1 Numa tubulação de 300 mm de diâmetro, a água escoa em uma extensão de 300 m, ligando um ponto A na cota topográfica de 90,0 m, no qual a pressão interna é de 275 kN/m2, a um ponto B na cota topográfica de 75,0 m, no qual a pressão interna é de 345 kN/m2. Calcule a perda de carga entre A e B, o sentido do escoamento e a tensão de cisalhamento na parede do tubo. Se a vazão for igual a 0,14 m3/s, calcule o fator de atrito da tubulação e a velocidade de atrito. pA = 275 kN/m2 pA/ = 275/9,8 = 28,06 m pB = 345 kN/m2 pA/ = 345/9,8 = 35,20 m L = 300 m ; ZA = 90 m ; ZB = 75 m ; Q = 0,14 m3/s a) Sentido de escoamento O sentido de escoamento é sempre dos níveis de energia mais elevada para a menos elevada. Como o diâmetro da tubulação é constante e sendo o escoamento permanente, a carga cinética em qualquer seção será a mesma. Deste modo, a linha de energia será paralela à linha piezométrica e a perda de carga entre A e B pode ser calculado pela diferença entre as cotas piezométricas das seções A e B. CPA = pA/ +ZA = 275/9,8 + 90,00 = 28,06 + 90 = 118,06 m CPB = pB/ +ZB = 345/9,8 + 75,00 = 35,20 + 75 = 110,20 m Como a CPA = 118,06 > CPB = 110,20 o sentido do escoamento será de A para B. b) Determinação da perda de carga entre A e B HAB = CPA – CPB = 118,06 – 110,20 = 7,86 m c) Determinação da tensão de cisalhamento na parede do tubo H = 4 L / D D/4 L = 9800. 7,86.0,30/4.300 = 19,26 kN/m2 d) Determinação da velocidade de atrito o u * = (19,26 / 1000)^,5 = 0,139 m/s e) Determinação do fator de atrito para Q = 0,14 m3/s V = (4Q/ D2) = (4 . 0,14/.0,30^2) V = 1,98 m/s g V D fL H 2 2 f = 2g . D . H / (L . V^2) = 19,6 . 0,30 . 7,86 / (300 . 1,98^2) f = 0,039 5 Página 22 exemplo 1.3 Considere um sistema de bombeamento como o da Figura 1.7, no qual uma bomba, com rendimento de 75%, recalca uma vazão de 15 l/s de água, do reservatório de montante, com nível d’água na cota 150,00 m, para ao reservatório de jusante, com nível d’água na cota 200,00 m. As perda de carga totais na tubulação de montante (sucção) e de jusante (recalque) são, respectivamente, Hm= 0,56 m e Hj=17,92 m. Os diâmetros das tubulações de sucção e recalque são, respectivamente, 0,15 m e 0,10 m. O eixo da bomba está na cota geométrica 151,50 m. Determine: a) as cotas da linha de energia nas seções de entrada e saída da bomba; b) as cargas de pressão disponíveis no centro dessas seções; c) a altura total de elevação e a potência fornecida pela bomba. 150 m 200 m A B C D a) Determinação das energias na entrada e saída da bomba Hentrada = Zm – Hm = 150 – 0,56 = 149,44 m Hsaída = Zj – Hj = 200 + 17,92 = 217,92 m b) Determinação das velocidades na entrada e saída da bomba Ventrada = (4Q/ Ds2) = (4.0,015/3,1415 . 0,15^2) = 0,85 m/s Vsaída = (4Q/ Dr2) = (4.0,015/3,1415 .0,10^2) = 1,91 m/s c) Determinação das pressões na entrada e saída HB = pB/ +ZB + VB^2/2g (na entrada) 149,44 = pB/ + 151,50 + 0,85^2/19,6 pB/ = -2,10m HC = pC/ +ZC + VC^2/2g (na saída) 217,92 = pC/ + 151,50 + 1,91^2/19,6 pC/= 66,23m d) Determinação da altura total de elevação da bomba H = HREC – HSUC = HC – HB = 217,92 – 149,44 = 68,48 m e) Determinação da potência da bomba Pot = QH/n = 9,8.0,015.68,48/0,75 = 13,42 kw ou 18,25 cv (1kw = 1,36cv) 6 Pág. 25 numero 1.11 Bombeiam-se 0,15 m3/s de água através de uma tubulação de 0,25 m de diâmetro, de um reservatório aberto cujo nível d’água mantido constante está na cota 567,00 m. A tubulação passa por um ponto alto na cota 587,00 m. Calcule a potência necessária à bomba, com rendimento de 75%, para manter no ponto alto da tubulação uma pressão disponível de 147 kN/m2, sabendo que, entre o reservatório e o ponto alto, a perda de carga é igual a 7,5 m. Dados: Q = 0,15 m3/s ; Htotal = 7,5 m D = 0,20 m ; n = 0,75 Pc = 147 kN/m2 pC/= 147/9,8 pC/= 15 m A B C D 587 m 567 m a) Determinação da energia cinética Vc = (4Q/ D2) = (4.0,15/3,1415 . 0,25^2) = 3,06 m/s Vc^2/2g = 3,06^2/19,6 = 0,477 m b) Determinação da altura manométrica H = (ZD – ZA) + (Hm + Hj) + (pD/ + VD^2/2g) ( energia disponível em D) H = (587 – 567) + ( 7,5 ) + (15 + 0,477) H = 42,98m c) Determinação da potência da bomba Pot = QH/n = 9,8.0,15.42,98/0,75 = 84,23 kw ou 114,56 cv 7 Pág. 25 numero 1.12 Entre os dois reservatórios mantidos em níveis constantes, encontra-se uma máquina hidráulica instalada em uma tubulação circular com área igual a 0,01 m2. Para uma vazão 20 l/s entre os reservatórios, um manômetro colocado na seção B indica uma pressão de 68,8 kN/m2 e a perda de carga entre as seções D e C é igual a 7,5 m. Determine o sentido do escoamento, a perda de carga entre as seções A e B, as cotas piezométricas em B e C, o tipo de máquina (bomba ou turbina) e a potência da máquina se o rendimento é de 80%. Resp. [AD;DHab=2,796m;CPb=7m;CPc=9,29m;bomba;Pot=,563kw] Dados: pB = 68,8 kN/m2 pB/ = 68,8/9,8 = 7 m A = 0,01 m2 ; HDC = 7,5 m ; Q = 0,020 m3/s ; n = 0,80 2,0 m 10,0 m D máquina C B A a) Sentido arbitrado: de A para B b) Determinação da energia cinética V = Q/A = 0,020/0,010 = 2,0 m/s V^2/2g = 2,0^2/19,6 = 0,20 m c) Determinação da HAB HA = HB + HAB pA/ + ZA + VA^2/2g = pB/ + ZB + VB^2/2g + HAB 0 + 10 + 0 = 7 + 0 + 0,20 + HAB HAB = 2,80 m d) Determinação da pC/ HC = HD + HCD pC/ + ZC + VC^2/2g = pD/ + ZD + VD^2/2g + HCD pC/ + 0 + 0,20 = 0 + 2 + 0 + pC/ = 9,30 m e) Determinação das cotas piezométricas em B e C CPB = pB/ + ZB = 7,00 + 0 = 7,00 m CPC = pC/ + ZC = 9,30 + 0 = 9,30 m f) Determinação da altura de elevação da bomba HB (sucção) = pB/ + ZB + VB^2/2g = 7 + 0 + 0,20 = 7,20 m HC (recalque) = pC/ + ZC + VC^2/2g = 9,3 + 0 + 0,20 = 9,50 m H = HC (recalque) - HB (sucção) = 9,50 – 7,20 = 2,30 g) Determinação da potência da bomba Pot = QH/n = 9,8.0,020.2,30/0,80 = 0,563 kw ou 0,766 cv 8 Pág. 26 numero 1.13 A vazão de água recalcada por uma bomba é de 4500 l/min. Seu conduto de sucção, horizontal, tem diâmetro de 0,30 m e possui um manômetro diferencial, como na Figura 1.11. Seu conduto de saída, horizontal, tem diâmetro de 0,20 m e sobre seu eixo, situado 1,22 m acima do precedente, um manômetro indica uma pressão de 68,6 kPa. Supondo o rendimento da bomba igual a 80%, qual a potência necessária para realizar este trabalho. Dado densidade do mercúrio dr = 13,6. Dados: Q = 4500 l/min = 4500/(1000.60) = 0,075 m3/s ; n = 0,80 P2 = 68,6 kN/m2 p2/ = 68,6/9,8 = 7 m Q Q Q 1,22 m P2 0,26m 0,18m Ds=0,30m Dr=0,20m a) Determinação da p1/ p/h.d = altura x densidade p1/= -0,26.1,0 - 0,18 . 13,6 p1/= -2,708 m b) Determinação das velocidades nas tubulações sucções e de recalque V1s = (4Q/ Ds2) = (4.0,075/.0,30^2) = 1,06 m/s V1/2g = 1,06^2/19,6 = 0,057 m V2r = (4Q/ Dr2) = (4.0,075/.0,20^2) = 2,38 m/s V2/2g = 2,38^2/19,6 = 0,291 m c) Determinação das cotas de energia na entrada e saída da bomba Hsucção = p1/ + Z1 + V1^2/2g = -2,708 + 0 + 0,057 = - 2,651 m Hrecalque = p2/ + Z2 + V2^2/2g = 7,0 + 1,22 + 0,291 = 8,511 m Helevação = Hsucção – Hrecalque = 8,511 – (-2,651) = 11,162 m d) Determinação da potência da bomba Pot = QH/n = 9,8.0,075.11,162/0,80 = 10,26 kw ou 13,95 cv 9 Pág. 26 numero 1.14 A Figura 1.12 mostra o sistema de bombeamento de água do reservatório R1 para o reservatório R2, através de uma tubulação de diâmetro igual a 0,40 m, pela qual escoa uma vazão de 150 l/s com uma perda de carga unitária J=0,055 m/m. As distâncias R1B1 e B1R2 medem, respectivamente, 18,5 m e 1800 m. A bomba B1 tem potência igual a 50 cv e rendimento de 80%. Com os dados da Figura 1.12, determine: a) a que distância de B1 deverá ser instalada B2 para que a carga de pressão na entrada de B2 seja igual a 2 mH2O; b) a potência da bomba B2, se o rendimento é de 80%, e a carga de pressão logo após a bomba. Despreze, nos dois itens, a carga cinética da tubulação. Dados: R1B1 = 18,50 m ; B1R2 = 1800 m ; Q = 0,15 m3/s ; n = 0,80 D = 0,40 m ; J = 0,0055 m/m ; Pot(B1) = 50 cv ; pD/ = 2 m 0,0 m B2 22,0 m D B1 R1 -2,0 m 15,0 m R2 B C D E F A C PA = 2 m C PB = -0 ,1 0 m C PC =1 9, 90 m C PD = 17 ,0 m C PE = 2 9 m C PF = 2 2 m a) Determinação da cota piezométrica em B HA = HB + HAB pA/ + ZA + VA^2/2g = pB/ + ZB + VB^2/2g + HAB 0 + 0 + 0 = pB/ + (-2) + 0 + 0,0055 . 18,5 pB/ = 1,90 m CPB = pB/ + ZB = 1,90 – 2 = - 0,10 m = HB (pois energia cinética = 0) b) Determinação da cota piezométrica em B Pot = Q (Hrec – Hsuc)/n = Q (HC – HB)/n = 50/1,36 = 9,8.0,15.(HC – 0,10) / 0,80 HC = 19,90 m = CPC CPC = pC/ + ZC 19,90 = pC/-2 pC/ = 21,90 m c) Determinação da distância de B1 em relação a B2 HC = HD + HCD pC/ + ZC + VC^2/2g = pD/ + ZD + VD^2/2g + HCD 19,90 = 2 + 15 + 0 + 0,0055 x x = 527,30 m d) Determinação da altura de elevação da bomba 2 HD = Hsuc = 2 + 15 + 0 HD = 17 m HE = HF + HEF HE = Hrec = 22 + (1800 – 527,30) 0,0055 HE = 29 m H = Hrec – Hsuc = HE – HD = 29 – 17 H = 12 m e) Determinação da potência da bomba 2 Pot (B2) = Q (Hrec – Hsuc)/n = Q (HE – HD)/n Pot (B2) = 9,8 . 0,15 (29 – 17)/0,80 = 22,05 kw (* 1,36) ou 30cv f) Determinação da pressão após a bomba B2 HE = pE/ + ZE = 29 = pE/+ 15 pE/ = 14 m 10 CAPÍTULO 2 CAPÍTULO 2 11 Pág. 59 exemplo 2.8 O sistema de abastecimento de água de uma localidade é feito por um reservatório principal, com nível d’água suposto constante na cota 812,00 m, e por um reservatório de sobras que complementa a vazão de entrada na rede, nas horas de aumento de consumo, com nível d’água na cota 800,00 m. No ponto B, na cota 760,00 m, inicia-se a rede de distribuição. Para que valor particular da vazão de entrada na rede, QB, a linha piezométrica no sistema é a mostrada na figura? Determine a carga de pressão disponível em B. O material das adutoras é de aço soldado novo (C=130). Utilize a fórmula de Hazem –Williams, desprezando as cargas cinéticas nas duas tubulações. Dados: 800 m C 812 m A 760 m B QB 6"650 m 4" 420 m a) Determinação da vazão (Q) 87,485,1 85,165,10 DC Q L H J J = (812 – 800)/(650 + 420) = (10,65Q ^1,85)/(130^1,85 . 0,15^4,87) Q = 0,02165 m3/s ou 21,65 litros/s Q = QB + QBC b) Determinação da vazão (QB) J = (812 – 800)/(650 + 420) = (10,65QBC ^1,85)/(130^1,85 . 0,10^4,87) QBC = 0,00745 m3/s ou 7,45 litros/s QB = Q - QBC = 21,65 – 7,45 = 14,20 litros/s c) Determinação da pressão no ponto B (pB/ CPB = pB/ + ZB = CPA - HAB HAB = J . L pB/ CPA - HAB – ZB = pB/ 812 – (812 – 800)/(650 + 420) . 650 - 760 pB/ = 812 - 0,011215 . 650 - 760 = 812 - 7,29- 760 = 44,71 m pB/ = 44,71 m 12 Pág. 63 numero 2.14 Em relação ao esquema de tubulações do Exemplo 2.8, a partir de que vazão QB, solicitada pela rede de distribuição de água, o reservatório secundário, de sobras, passa a ser também abastecedor. Dados: C = 130 800 m C 812 m A 760 m B QB 6"650 m 4" 420 m a) Considerações iniciais Na iminência do reservatório 2 abastecer o ponto B a cota de energia em C (HC) é igual à cota de energia no ponto B (HB). Como as cargas cinéticas são desprezadas, a cota piezométrica em C é igual em B, ou seja: CPB = CPC mas CPB = CPA - HAB HAB = CPA – CPC Ainda tem-se que, como CPC = CPB HBC = 0 QC = 0 Q = QAB + QBC = QAB + 0 Q = QAB Logo, o único fluxo que ocorre é na tubulação do trecho AB. b) Determinação da vazão em B limite para que R2 abasteça em B 87,485,1 85,165,10 DC LQ H (812 – 800) = 10,65.QAB^1,85.650/(130^1,85 . 0,15^4,87) QAB = 0,0283 m3/s ou 28,3 litros/s 13 Pág. 67 numero 2.33 Determinar a relação entre a vazão máxima e a vazão mínima que pode ser retirada na derivação B, conforme a figura, impondo que o reservatório 2 nunca seja abastecido pelo reservatório 1 e que a mínima carga de pressão disponível na linha seja 1,0 mH20. Utilize a fórmula de Hazen-Williams. Despreze as perdas localizadas e as cargas cinéticas. 552 m 549 m 12" 850 m C = 100 450 m 1 2 8" C = 110 C 554 m A B QB 2 Caso 1 Caso a) Considerações para o 1 Caso No 1 caso de vazão mínima o R2 está na iminência de ser abastecido mas ainda não abastece o ponto B a cota de energia em C (HC) é igual à cota de energia no ponto B (HB). Como as cargas cinéticas são desprezíveis CPB = CPC mas CPB = CPA - HAB HAB = CPA – CPC b) Determinação da vazão em B limite para que R2 abasteça em B 87,485,1 85,165,10 DC LQ H (554 – 552) = 10,65.QAB^1,85.850/(110^1,85 . 0,30^4,87) QABmin = 0,0488 m3/s ou 48,8 litros/s (vazão mínima) c) Considerações para o 2 Caso No 2 caso de vazão máxima o R2 também abastece o ponto B, contanto que a pressão mínima na rede seja de (p/min = 1 m. Como as cargas cinéticas são desprezíveis, tem-se que: HB = CPB = CPA - HAB e ainda CPB = CPC - HCB CPB = pB/ + ZB = (p/minm Logo: HAB = CPA – CPB = 554 – 550 HAB = 4 m HCB = CPC – CPB = 552 – 550 HCB = 2 m QB = QAB + QCB d) Determinação da QAB 87,485,1 85,165,10 DC LQ H HAB = (554 – 550) = 10,65.QAB^1,85.850/(110^1,85 . 0,30^4,87) QAB = 0,0710 m3/s ou 71,0 litros/s e) Determinação da QCB 87,485,1 85,165,10 DC LQ H HCB = (554 – 552) = 10,65.QCB^1,85.450/(100^1,85 . 0,20^4,87) QCB = 0,0215 m3/s ou 21,5 litros/s f) Determinação da vazão máxima QB = QAB + QCB = 71,0 + 21,5 = 92,5 litros/s g) Relação Qmáx/Qmin Qmáx/Qmin = 92,5/48,8 Qmáx/Qmin =1,89 14 Pág. 67 numero 2.34 Uma tubulação de 0,30 m de diâmetro e 3,2 km de comprimento desce, com inclinação constante, de um reservatório cuja superfície livre está a uma altitude de 120 m, conectando-se aos reservatórios em ponto situados a 10 m abaixo de suas respectivas superfícies livres. A vazão através da linha não é satisfatória e instala-se uma bomba na altitude 135 m a fim de produzir o aumento de vazão desejado. Supondo que o fator de atrito da tubulação seja constante e igual a f = 0,20 e que o rendimento da bomba seja de 80%, determine: a) a vazão original do sistema por gravidade; b) a potência necessária à bomba para recalcar uma vazão de 0,15 m3/s; c) as cargas de pressão imediatamente antes e depois da bomba, desprezando as perdas de carga localizadas e considerando a carga cinética na adutora; d) desenhe as linhas de energia e piezométrica após a instalação da bomba, nas condições do item anterior. Dados: D = 0,30m ; f = 0,020 ; n = 0,80 ; L = 3200 m ; Q = 0,15 m3/s 120 m D 150 m A 135 B 1 2 140 110 C a) Determinação da vazão original sem bombeamento (Q) g V D fL H 2 2 (140– 110) = 0,020.3200.V^2/(0,30.19,6) V = 1,66 m/s Q = ( D^2/4)V Q = 0,30^2 / 4 . 1,66 Q = 0,117 m3/s b) Potência do sistema com bombeamento para Q = 0,15 m3/s V = (4Q/ D2) = (4 . 0,15/.0,30^2) = 2,12 m/s g V D fL H 2 2 H = 0,020 . 3200 . 2,12^2/(0,30 . 19,6) H = 48,92 m -A altura de elevação é: H = ZJ – ZM + H = 110 – 140 + 48,92 = 18,92 m Pot = QH/n = 9,8.0,15.18,92/0,80 = 34,76 kw ou 74,28 cv c) Determinação da perda de carga entre A e B antes da bomba 140 - 135 = 5 m x g V D fL H 2 2 HAB = 0,020 . 533,33 . 2,12^2 / (0,30 . 19,6) = 8,15 m d) Carga de pressão antes da bomba HA = HB + HAB pA/ + ZA + VA^2/2g = pB/ + ZB + VB^2/2g + HAB 0 + 150 + 0 = pB/ + 135 + 2,12^2/19,6 + 8,15 pB/ = 6,62 m e) Determinação da perda de carga entre C e D depois da bomba HCD = 0,020 . (3200-533,33) . 2,12^2 / (0,30 . 19,6) = 40,76 m f) Carga de pressão depois da bomba HC = HD + HCD pC/ + ZC + VC^2/2g = pD/ + ZD + VD^2/2g + HAB pC/ + 135 + 2,12^2/19,6 = 0 + 120 + 0 + 40,76 pC/ = 25,53 m sen a = (150-120)/3200 = 0,009375 sen a = (140 – 135)/x x = 533,33m 15 Pág. 68 numero 2.35 Na figura abaixo os pontos A e B estão conectados a um reservatório em nível constante e os pontos E e F conectados a outro reservatório também mantido em nível constante e mais baixo que o primeiro. Se a vazão no trecho AC é igual a 10 l/s de água, determinar as vazões em todas as tubulações e o desnível H entre os reservatórios. A instalação está em um plano horizontal e o coeficiente de rugosidade da fórmula de Hazen-Williams, de todas as tubulações, vale C = 130. Despreze as perdas de carga localizadas e as cargas cinéticas nas tubulações. A 300 m 6" C 6" E FB 200 m 250 m 100 m 100 m 6" 4" 8" D QAC = 10 l/s a) Determinação das vazões QAC, QBC e QCD Como HAC = HBC e LAC = LBC 87,485,1 85,165,10 DC LQ H = 87,485,1 85,165,10 DC LQ H QBC = QAC (DBC/DAC)^2,63 = 10 . (6/4)^2,63 = 29 litros/s Como QCD = QAC + QBC = 10 + 29 = 39 litros/s b) Determinação das vazões QDE e QDF Como HDE = HDF e DDE = DDF 87,485,1 85,165,10 DC LQ H = 87,485,1 85,165,10 DC LQ H QDE = QDF (LDF/LDE)^(1/1,85) = QDF . (250/200)^(1/1,85) = QDE = 1,128 QDF Como QCD = QDE + QDF = 1,128QDE + QDE QCD = 2,128 QDE 39 = 2,128 QDF QDF = 39/2,128 QDF = 18,32 litros/s QDE = 1,128 . QDF = 1,128 . 18,32 QDE = 20,66 litros/s c) Determinação das perdas de carga Em C JAC = (10,65.0,010^1,85)/(130^1,85 . 0,010^4,87) = 0,0193m/m HAC = JAC . LAC = 0,0193 . 100 = 1,93 m Em D JCD = (10,65.0,039^1,85)/(130^1,85 . 0,20^4,87) = 0,0082m/m HAC = JAC . LAC = 0,0082 . 300 = 2,46 m Em E JDE = (10,65.0,0206^1,85)/(130^1,85. 0,15^4,87) = 0,0103m/m HDE = JDE . LDE = 0,0103 . 200 = 2,06 m d) Determinação das cotas piezométricas HA = HC + HAC = HA = (HD + HCD) + HAC HA = (HE + HDE) + HCD + HAC HA – HE = HDE + HCD + HAC H = 2,06 + 2,46 + 1,93 H = 6,45 m e) Esquema do fluxo A ou E C D E ou F 16 Pág. 68 numero 2.36 Determinar o valor da vazão QB, e a carga de pressão no ponto B, sabendo que o reservatório 1 abastece o reservatório 2 e que as perdas de carga unitárias nas duas tubulações são iguais. Material: aço soldado revestido com cimento centrifugado. Despreze as perdas localizadas e as cargas cinéticas. C = 140 800 m C 810 m A 780 m B QB 6"860 m 4" 460 m 1 2 a) Relação entre as vazões 87,485,1 85,165,10 DC LQ H = 87,485,1 85,165,10 DC LQ QAB/QBC = [(DAB/DBC)^4,87]^(1/1,85) QAB/QBC = (DAB/DBC)^2,63 QAB/QBC = (6/4)^2,63 = 2,905 QAB = 2,905 QBC Como QAB = Qbomba + QBC 2,905QBC = Qbomba + QBC Qbomba = 1,905 QBC b) Determinação da vazão QAB e QBC JAB = HAB/L = (810-800)/(860 + 460) = 10,65.QAB^1,85/(140^1,85.0,15^4,87) = 0,00757 QAB = 0,01886 m3/s ou 18,86 litros/s QBC = QAB/2,905 = 0,01886 / 2,905 = 0,0065 m3/s ou 6,5 litros/s c) Determinação da vazão Qbomba Qbomba = QAB – QBC = 18,86 – 6,50 = 12,36 litros/s d) Determinação da perda de carga entre A e B HAB = JAB . LAB = 0,00757 . 860 = 6,51 m e) Determinação da pressão em B (pB/ HA = HB + HAB pA/ + ZA + VA^2/2g = pB/ + ZB + VB^2/2g + HAB 0 + 810 + 0 = pB/ + 780 + 0 + 6,51 pB/ = 23,49 m 17 CAPÍTULO 3 CAPÍTULO 3 18 Página 85 exemplo 3.3 Na instalação hidráulica predial mostrada na Figura 3.15, a tubulação é de PVC rígido, soldável com 1” de diâmetro, e é percorrida por uma vazão de 0,20 l/s de água. Os joelhos são de 90O e os registros de gaveta, abertos. No ponto A, 2,10 m abaixo do chuveiro, a carga de pressão é igual a 3,3 mH20. Determine a carga de pressão disponível imediatamente antes do chuveiro. Os tês estão fechados em uma das saídas. Dados: PVC rígido soldável D = 1” = 0,1202 (pág. 57) Q = 0,20 l/s ; CPA = 3,30 m 3,0 m 1,2 m 0,9 m 3,5 m A a) Determinação dos comprimentos equivalentes totais das conecções Acessório Compr. Equivamente (m) 3 joelhos de 90o 3 . 1,5 = 4,50 2 registros de gaveta abertos 2 . 0,3 = 0,60 Tê passagem direta 0,9 = 0,90 Tê lateral 3,1 = 3,1 Comprimento real 8,60 Comprimento Total 17,70 b) Determinação da perda de carga total H = J . L J = Q1,75 c) Determinação Cota piezométrica antes do chuveiro CPCH = CPA - H CPCH = 3,30 – (0,1202 . 0,201,75) . 17,70 CPCH = 3,17 m d) Determinação pressão no chuveiro CPCH = pCH/+ ZCH pCH/ = CPCH - ZCH = 3,17 – 2,10 = 1,07 m pCH/ = 1,07 m 19 Página 87 exemplo 3.4 Na instalação hidráulica predial mostrada na figura, as tubulações são de aço galvanizado novo, os registros de gávea são abertos e os cotovelos têm rio curto. A vazão que chega ao reservatório C é 38% maior que a que escoa contra a atmosfera novo ponto C. Determine a vazão que sai do reservatório A, desprezando as cargas cinéticas. 6,0 6,0 3,0 D 5,0 A 0,3 1,0 C 1"1 1 2" 1 12" 1,0 B a) Determinação dos comprimentos equivalentes das conecções Trecho BC Trecho BD Acessório Comp. Equi.(m) Acessório Comp. Equi.(m) Te lateral (1 1/2”) 2,587 Te lateral (1 1/2”) 2,587 Reg. Gaveta 0,175 2 cotovelos 90º 2,550 Saída canalização 0,775 Reg. Gaveta 0,263 Comprimento Real 6,00 Saída canalização 1,133 Comprimento real 7,30 Comprimento total 9,54 (LBC) Comprimento total 13,83 (LBD) b) Determinação das cotas piezométricas Seja X a cota piezométrica imediatamente antes do tê localizado em B. Para os dois ramos da instalação, tem-se as seguintes perdas totais: HB = HD + HBD e HB = HC + HBC HB = HB HD + HBD = HC + HBC 3 + HBD = 1 + HBC HBC = HBD + 2 portanto JBC . LBC = JBD . LBD + 2 H = J . L J = Q1,75 c) Determinação das vazões Como QBD = 1,38 QBC e pela tabela 2.5 pag. 57 JBC . LBC = JBD . LBD + 2 0,3044 QBC^1,88 . 9,54 = 0,03945 (1,38 . QBC)^1,88 . 13,83 + 2 2,904 QBC^1,88 = 0,996 QBC ^1,88 + 2 QBC = 1,03 litros/s QBD = 1,42 litros/s Logo, a vazão que sai do reservatório A será a soma: QBC + QBD = 2,45 litros/s 20 Pág. 88 numero 3.1 A instalação mostrada na Figura tem diâmetro de 50 mm em ferro fundido com leve oxidação. Os coeficientes de perdas de carga localizadas são: entrada e saída da tubulação K = 1,0, cotovelo 90º K = 0,90, curvsa de 45º K = 0,20 e registro de ângulo, aberto, K = 5,0. Determine, usando a equação de Darcy-Weisbach: a) a vazão transportada: b) querendo-se reduzir a vazão párea 1,96 litros/s, pelo fechamento parcial do registro, calcule qual deve ser a perda de carga localizada no registro e seu comprimento equivalente. 45,0 50,0 13,0 m 25,0 m 5,0 m 2,0 m a) Determinação da velocidade g v k g v D L fZ 22 22 (Darcy) (50 – 45) . 19,6 = [f 45/0,05 + ((2*1 +0,9 + 2*0,20+5)v^2 98 = (900 f + 8,30) v^2 ; v = ? e f = ? Processo interativo (chute inicial) J = (Z = H)/L = 5 / 45 = (0,111 m/m) * 100 J = 11,11 (m/100m) Tabela 2 A2 pag. 203 e = 0,30 v = 1,80 m/s e f = 0,0333 Para v = 1,80 m/s e f = 0,0333 (900 * 0,0333 + 8,3) 1,8^2 = 123,99 # 98 Para v = 1,60 m/s e f = 0,0334 (900 + 0,0334 + 8,3) 1,6^2 = 98,2 = 98 ok Logo: v = 1,60 m/s e f = 0,0334 b) Determinação da vazão Q = ( D^2/4) . v = 0,05^2/4 . 1,60 = Q = 0,00314 m3/s c) Determinação da velocidade para Q = 1,96 litros/s v = 4 Q / D^2 = 4 . 0,00196 / 0,05^2 v = 1,0 m/s d) Determinação do coeficiente de perda de carga do registro (kreg) 2g . z/ v^2 = f . L/D + (kreg + k) 19,6 (50 – 45) / 1^2 = 0,0341 . 45/0,05 + (kreg + 3,3) 98 = 30,69 + kreg + 3,30 kreg = 64,01 e) Determinação da perda de carga do registro para Q = 1,96 litros/s h = k v^2/2g = 64,01 . 1^2/19,6 h = 3,26 m f) Determinação do comprimento equivalente do registro Le/D = k/f Le = k . D/f = 64,01 . 0,05/0,0341 Le = 93,86 m 21 Pág. 89 numero 3.3 Uma adutora de 500 mm de diâmetro, 460 m de comprimento, em aço soldado revestido de cimento centrifugado, liga dois reservatórios mantidos em níveis constantes. Determine a capacidade de vazão da adutora quando o desnível entre os reservatórios for de 3,50 m, nas seguintes condições: a) desprezando as perdasde carga localizadas na entrada e na saída da tubulação; b) considerando tais perdas de carga localizadas, adotando os seguintes coeficientes de perdas Ke = 0,5 e Ks = 1,0. Faça comentários pertinentes sobre os resultados encontrados, observando a relação entre o comprimento e o diâmetro da adutora. a) Determinação da velocidade g v k g v D L fZ 22 22 2g.Dz = 19,5 . 3,5= (460/0,50 . f + 0) v^2 68,6 = 920 f. v^2 Interação inicial J = Dz=Dh/L = 3,5/400 = 0,0076 m/m Ou 0,761 m/100m e e = 0,10 e D = 500 mm TAB. A2 pág. 214 2,20 m/s v = 2,20 m/s TAB. A1 pag. 202 f = 0,0147 68,6 ≠ 920 . 0,0147 . 2,2^2 = 65,45 não convergiu Para v = 2,25 m/s f = 0,0147 68,6 = 920 . 0,0147 . 2,25^2 =68,46 ok convergiu b) Determinação da vazão Q = v . 3,14 . D^2/4 = 2,25 . 3,14 . 0,5^2/4 = 0,442 m3/s c) Det. vazão considerando perdas de cargas localizadas Ke = 0,50 Ks = 1,0 g v k g v D L fZ 22 22 68,6 = (0,0147*460/0,5 + (1+0,5))v^2 v = 2,14 m/s Q = v . 3,14 . D^2/4 = 2,14 . 3,14 . 0,5^2/4 = 0,420 m3/s 22 Pág. 89 numero 3.4 Em um distrito de irrigação, um sifão de 2” de diâmetro possui as dimensões indicadas na figura e é colocado sobre um dique. Estime a vazão esperada sob uma carga hidráulica de 0,50 m e a carga de pressão disponível no ponto médio do trecho horizontal do sifão. Adote os seguintes coeficientes de perda de carga localizada: entrada Ke = 0,5, saída Ks = 1,0, curva de 45º K = 0,2. Material da tubulação ferro fundido com revestimento asfáltico. Utilize a equação de Darcy – Weisbach. Material: ferro fundido com revestimento asfáltico e = 0,15 mm 1,8 m1,8 m 0,50 1,2 m50,0 50,5 49,5 a) Determinação da velocidade g v k g v D L fZ 22 22 para D = 50 mm e = 0,15 mm 0,50*919,6 = [ f 480/0,05 + (0,5 + 1,0 + 2*0,2) v^2 Tentativa inicial J = Dz/L = 0,50/4,80 = 0,1042 m/m ou 10,42 m/100m Pela Tabela A2 v = 1,90 m/s e f = 0,0278 9,8 = (96 * 0,0278 + 1,90) * 1,90^2 = 16,49 # 9,8 Para v = 1,46 m/s e f = 0,0281 9,8 = (96 * 0,0281 + 1,9) 1,46^2 = 9,8 = 9,8 ok Logo v = 1,46 m/s e f = 0,0281 b) Determinação da vazão Q = ( D^2/4) v = 0,050^2/4 * 1,46 = 0,00286 m3/s ou Q = 2,90 litros/s c) Determinação da perda de carga até o trecho horizontal g v k g v D L fHAB 22 22 = (0,0281 * 2,3/0,05 + 0,7) * 1,46^2/19,6 HAB = 0,216 m d) Determinação da pressão no trecho horizontal HA = HB + HAB pA/ + ZA + VA^2/2g = pB/ + ZB + VB^2/2g + HAB 0 + 50 + 0 = pB/ + 50,5 + 1,46^2/19,6 + pB/ = 0,83 m 23 Pág. 91 numero 3.8 Dois reservatórios, mantidos em níveis constantes, são interligados em linha reta através de uma tubulação de 10 m de comprimento e diâmetro D = 50 mm, de PVC rígido, como mostra o esquema da figura. Admitindo que a única perda de carga localizada seja devido à presença de um registro de gaveta parcialmente fechado, cujo comprimento equivalente é Le = 20,0 m, e usando a fórmula de Hazen- Williams, adotando C = 145, determine: a) a vazão na canalização supondo que o registro esteja colocado no ponto A; b) Idem, supondo o registro colocado no ponto B; c) a máxima e a mínima carga de pressão na linha, em mH2O, nos casos a e b; d) Desenhe em escala as linhas piezométrica e de energia. Considerem, em ambos os casos, a carga cinética na tubulação. NA NA (A) 1,0 m 1,0 m 3,0 m (D) (E) (C) (F) (G) (B) a) Determinação da vazão HC = HH + HCH ( = H distribuída + H localizada) pC/ + ZC + VC^2/2g = pH/ + ZH + VH^2/2g + HCH 0 + 4 + 0 = 0 + 1 + 0 + HCH 87,485,1 85,165,10 DC LQ H = HCH (4 – 1) = 10,65 . Q^1,85 . (10 + 20) / [145^1,85 . 0,05^4,87] QA = 0,00437 m3/s ou 4,37 litros/s = QB b) Determinação da velocidade na canalização v = 4 Q/ D^2 = 4 . 0,00437 / (3,14 . 0,05^2) = 2,22 m/s c) Determinação das pressões na linha (Registro no ponto A) Em D HC = HD + HCD pC/ + ZC + VC^2/2g = pD/ + ZD + VD^2/2g + HCD 0 + 4 + 0 = pD/ + 3 + 2,22^2/19,6 + 0 pD/ = 0,75 m Em E HC = HE + HCE pC/ + ZC + VC^2/2g = pE/ + ZE + VE^2/2g + HCE 0 + 4 + 0 = pE/ +3+2,22^2/19,6+10,65.Q^1,85 . 20)/[145^1,85 . 0,05^4,87] pE/ = - 1,25 m Em B HC = HB + HCB pC/ + ZC + VC^2/2g = pB/ + ZB + VB^2/2g + HCB 0 + 4 + 0 = pB/ +0+2,22^2/19,6+10,65.Q^1,85 (10+20)/[145^1,85. 0,05^4,87] pB/ = 0,75 m d) Descrição das pressões extremas no caso do registro no ponto A (pD/ )máxima = 0,75 m e (pE/)min = -1,25 m e) Esquema de distribuição de pressão na linha (A) (D) (E) (C) (F) (G) (B) 0,75m -1,25m 0,75m 24 Pág. 91 numero 3.8 (continuação) f) Esquema do caso do registro no ponto B NA NA (A) 1,0 m 1,0 m 3,0 m (D) (E) (C) (F) (G) (B) g) Determinação das pressões na linha (Registro no ponto B) Em A HC = HA + HCA pC/ + ZC + VC^2/2g = pAD/ + ZA + VA^2/2g + HCA 0 + 4 + 0 = pA/ + 3 + 2,22^2/19,6 + 0 pA/ = 0,75 m Em E HC = HE + HCE pC/ + ZC + VC^2/2g = pE/ + ZE + VE^2/2g + HCE 0 + 4 + 0 = pE/ +3+2,22^2/19,6+10,65.Q^1,85 . 20)/[145^1,85 . 0,05^4,87] pE/ = - 1,25 m Em F HC = HF + HCF pC/ + ZC + VC^2/2g = pF/ + ZF + VF^2/2g + HCF 0 + 4 + 0 = pF/ +0+2,22^2/19,6+10,65.Q^1,85 (10)/[145^1,85. 0,05^4,87] pF/ = 2,75 m Em G HC = HG + HCG pC/ + ZC + VC^2/2g = pG/ + ZG + VG^2/2g + HCG 0 + 4 + 0 = pG/ +0+2,22^2/19,6+10,65.Q^1,85 (10+20)/[145^1,85. 0,05^4,87] pG/ = 0,75 m h) Determinação das pressões extremas no caso do registro no ponto B (pF/ )máxima = 2,75 m e (pE/)min = 0,75 m i) Esquema de distribuição de pressão na linha (A) 1,0 m 1,0 m (D) (E) (C) (F) (G) (B) 0,75m 0,75m 2,75m 25 Pág. 92 numero 3.11 O reservatório B, prismático de área igual a 1,0 m2, possui um orifício no fundo que abre comandado pelo manômetro, quando este acusar este acusar uma pressão de 4,9 kPa, conforme a figura. Qual deve ser a cota do nível d’água no reserva tório A, mantido em nível constante, para que o orifício do reservatório B seja aberto 10 min após a abertura do registro de gaveta da canalização de 1” de diâmetro e os joelhos de 90º . No tempo t = 0, o reservatório B está vazio. Considere a carga cinética. Dados: AB = 1 m2 ; pB = 4,90 kPa = 4,9/9,8 = 0,50m ; dt = 10 min = 600s ? 0,6 m 0,0 m A B 0,5 m 1,0 m 1,0 m 1,0 m 0,5 m 0,2 m a) Idealização Para que a válvula do reservatório B seja aberta em 10 min, até encher a cota B em 1,64 ft. b) Determinação da vazão e velocidade Q = volume/tempo = (1 . 0,50) / 600 = 0,000833 m3/s v = 4Q/ D^2 = 4 . 0,000833/0,025^2 v = 1,70 m/s h (localizada)= k v^2/2g = (1 + 6 . 0,9 + 0,2 + 1) v^2/2g = 0,388 v^2 = 0,388 . 1,70 = 1,121 m c) Determinação da perda de carga distribuída h (distribuída) = f(L/D) v^2/2g = f . 4,20/0,025 . 1,70^2/19,6 = 24,77 f e/D = 0,00001/0,025 = 0,00040 e Rey = V . D/v = 1,70 . 0,025/10-6 = 4,20. 105 f = 0,0170 h (distribuída) = f(L/D) v^2/2g = 24,77 . f = 24,77 . 0,0170 = 0,421 m d) Determinação da perda de carga total H = h (localizada) + h (distribuída) H = 1,121 + 0,421 = 1,54 m e) Determinação da altura do NA do reservatório A HA = HB + HAB pA/ + ZA + VA^2/2g = pB/ + ZB + VB^2/2g + HAB 0 + ZA + 0 = 0 + 0,50 + 1,70^2/19,6 + 1,54 ZA = 2,18 m 26 Pág. 92 numero 3.13 Sabendo-se que as cargas de pressão disponíveis em A e B são iguais e que a diferença entre as cargas de pressão em A e D é igual a 0,9 mH2O, determine o comprimento equivalente do registro colocado na tubulação de diâmetro único, assentada com uma inclinação de 2º em relação a horizontal, conforme figura. D CB A 200 m 200 m 2o a) Determinação da energia cinética na tubulação HA = HB + HAB pA/ + ZA + VA^2/2g = pB/ + ZB + VB^2/2g + HAB Como pA/ = pB/ e VA = VB HAB = ZA – ZB = f L/D . v^/2g 200 . sen2o = f . 200/D v^2/2g v^2/2g = sen 2o . D/f b) Determinação do comprimento equivalente do registro HA = HD + HAD pA/ + ZA + VA^2/2g = pD/ + ZD + VD^2/2g + HAD Como pA/ - pD/ = 0,90 m e VA = VD (pA/ - pD/ ) + (ZA – ZD) = [f/D (L+X(REG))] . v^2/2g 0,90 + 400 sen 2o = [(400 + X) . f/D] . sen 2o . D/f 0,90 + 13,96 = [400 + X] sen 2o X = [(0,90 + 13,96)/sen 2o] – 400 X = 25,79 m 27 CAPÍTULO 4 CAPÍTULO 4 28 Pág. 100 exemplo 4.1 Na tubulação mostrada na figura, com 6” de diâmetro e coeficiente de atrito f = 0,022, a pressão em A vale 166,6 kN/m2 e D vale 140,2 kN/m2. Determine a vazão unitária de distribuição em marcha q, sabendo que a tubulação está no plano vertical e que a vazão no trecho AB é de 20 l/s. Despreze as perdas localizadas. 2 m q =? 20 l/s 120 m 39 m B 2 m 82 m D C A Dados: D = 0,115 m ; f = 0,022 ; pA = 166,6 kN/m2 pA/ = 166,6/9,8 = 17,00 m Q = ? ; QAB = 20 l/s ; pD = 140,2 kN/m2 pD/ = 140,2/9,8 = 14,31 m ou pD/= 140,2.10^3/9,8.10^3 = 14,31 m v = 4.Q/3,14.D^2 = 4.0,02/3,14.0,15^2 = 1,13 m/s a) Determinação da energia específica EA = zA + pA/g + vA^2/2g = 1 + 17 + 1,13^2/19,6 = 18,06 m ED = zD + pD/g + vD^2/2g = 2 + 14,31 + vD^2/19,6 = 16,31 + vD^2/19,6 EA – ED = DHAB + DHBC + DHCD = DHAD DHAD = EA – ED = JAB.Lab + JBC.LBC + JCD.LCD = 18,06 – 16,31 + vD^2/2g = 1,75 – 4QD/(3,14.0,15^2) = = 0,0827 . 0,022/0,15^5 . (QAB^2.LAB + QBC^2.LBC + QCD^2.LCD) 1,75 – 163,54QD^2 = 23,96(0,02^2 . 40 + 120.Qf^2 + 84.Qj^2) Mas QD = Qj 1,75 – 163,54Qj^2 = 0,383 + 2875,10.Q^2 + 2012,57.Qj^2) 1,367 = 2875,10 . Qf^2 + 2176,11 . Qj^2 (I) b) Determinação da vazão Qj Qf = (Qm + Qj)/2 = (0,020 + Qj)/2 De (I), tem-se; 1,367 = 718,775 . (0,02 + Qj)^2 + 2176,11.Qj^2 Qj = 0,015 m3/s c) Determinação de Qf Qf = (Qm + Qj)/2 = (0,020 + 0,015)/2 Qf = 0,0175 m3/s d) Determinação da distribuição em marcha (q) q = Qd/L = (Qm – Qj)/L = (0,020 + 0,015)/120 q = 4,17.10^-5 m3/s/m Ou q = 0,0417 litros/s/m 29 Pág. 105 exemplo 4.2 A ligação de dois reservatórios mantidos em níveis constantes é feita pelo sistema de tubulações mostrado na figura. Assumindo um coeficiente de atrito constante para todas as tubulações é igual a f = 0,020, desprezando as perdas localizadas e as cargas cinéticas, determine a vazão que chega ao reservatório R2, as vazões nos trechos d 4” e 6” e a pressão disponível no ponto B. 573,00 593,00 A R1 C R2 8" 750 m 4" 600 m 6" 544,20 B 900 m a) Determinação do comprimento equivalente do trecho AB Tubulação em paralelo ii i EE E Lf D Lf D .. 55 (8^5/Lê)^0,5 = (4^5/600)^0,5 + (6^5/750)^0,5 Lê = 1600 m b) Determinação da vazão 5 2 0827,0 D fLQ H H = 20 = 0,0827 . 0,020 . 2500 . Q^2/0,20^5 Q = 0,0393 m3/S Ou Q = 39,3 litros/s c) Determinação da cota piezométrica em B (CPB) CPB = pB/ + ZB ou CPB = CPA – HAB ou CPB = CPC + HBC CPB = 573 + 0,0827 . 0,020 . 900 . 0,0393^2/0,20^5 CPB = 580,20 m d) Determinação da vazão na tubulação de D = 4” CPA = CPB + HAB 593 = 580,20 + 0,0827 . 0,020 . 600 . Q4^2/0,10^5 Q4 = 0,0114 m3/s e) Determinação da vazão na tubulação de D = 6” CPA = CPB + HAB 593 = 580,20 + 0,0827 . 0,020 . 750 . Q4^2/0,15^5 Q6 = 0,0280 m3/s ou Q = 0,0393 = 0,0114 + Q6 Q6 = 0,0280 m3/s f) Determinação da pressão no ponto B (pB/) CPB = pB/ + ZB pB/ = CPB – ZB pB/ = 580,20 – 544,20 pB/ = 36 metros ou 352,80 kN/m2 30 Pág. 109 exemplo 4.3 Uma instalação de transporte de água compreende dois reservatórios A e D, abertos e mantidos em níveis constantes, e um sistema de tubulações de ferro fundido novo, C=130, com saída livre para a atmosfera em C. No conduto BD, e logo a jusante de B, está instalada uma bomba com rendimento igual a 75%. Determine a vazão bombeada para o reservatório D quando o conduto BC deixa sair livremente uma vazão de 0,10 m3/s e ter uma distribuição de vazão em marcha com taxa (vazão unitária de distribuição) q = 0,00015 m3/(s.m). Determine também a potência necessária à bomba. Despreze as perdas localizadas e a carga cinética nas tubulações. Trata-se de uma aplicação conjunta dos conceitos de distribuição em marcha, problema dos três reservatórios e bombeamento. Como visto no item anterior, a questão importante para a resolução do problema é a determinação da cota piezométrica no ponto de bifurcação, ponto B. 36,00 30,0 A D Bomba D3 = 0,2 0 m 400 m D2 = 0,30 m 810 m D1 = 0,40 m B 20 0 m 20,00 C a) Determinação da vazão fictícia no trecho BC QmBC = QjBC + q . L = 0,10 + 0,00015 . 400 QmBC = 0,16 m3/s QfBC = (QmBC + QjBC)/2 = (0,10 + 0,16)/2 QfBC = 0,13 m3/s b) Determinação da perda de carga HBC 87,485,1 85,165,10 DC LQ H = 10,65 . 0,13^1,85 . 400/(130^1,85 . 0,30^4,87) = HBC = 4,22 m c) Determinação da cota piezométrica em B (CPB) CPB = CPC + HBC CPB = (pC/ + ZC) + HBC = (0 + 20) + 4,22 = 24,22 m d) Determinação da vazão no trecho AB (QAB) CPB = CPA - HAB HAB = CPA – CPB = 30 – 24,22 = 5,78 HAB = 5,78 = 10,65 . QAB^1,85 . 810/(130^1,85 . 0,40^4,87) = QAB = 0,224 m3/s e) Determinação da vazão no trecho BD (QBD) QAB = QBC + QBD QBD = QAB – QBC = 0,225 – 0,130 QBD = 0,065 m3/s f) Determinação da altura manométrica HM = HREC – HSUC; como v^2/2g = 0 H = CP HSUC = CPB = 24,22 m CPD = ZD + HDB = HREC HREC = 36 + 10,65 . 0,065^1,85 . 200/(130^1,85 . 0,20^4,87) = HREC = 36 + 4,22 = 40,22 m g) Determinação da potência da bomba n HHQ Pot sucçãocalque )( Re Pot = (9,8 . 0,065 . (40,22-24,22)/0,75 = Pot = 13,58 kw ou 18,48 cv 31 Pág. 117 numero 4.1 Um sistema de distribuição de água é feito por uma adutora com um trecho de 1500 m de comprimento e 150 mm de diâmetro, ambos como mesmo fator de atrito f = 0,028. A vazão total que entra no sistema é 0,025 m3/s e toda água é distribuída com uma taxa uniforme por unidade de comprimento que (vazão de distribuição unitária) nos dois trechos, de modo que a vazão na extremidade de jusante seja nula. Determine a perda de carta total na adutora, desprezando as perdas localizadas ao longo da adutora. 32 Pág. 118 numero 4.2 Por uma tubulação de 27” de diâmetro e 1500 m de comprimento, passa uma vazão de 0,28 m3/s de água. Em uma determinada seção, a tubulação divide-se em dois trechos iguais de 18” de diâmetro, 3000 m de comprimento, descarregando livremente na atmosfera. Em um destes trechos, toda a vazão que entra na extremidade de montante é distribuída ao longo da tubulação, com uma vazão por unidade de comprimento uniforme e, no outro, metade da vazão que entra é distribuída uniformemente ao longo do trecho. Adotando para todas as tubulações um fator de atrito f = 0,024 e supondo que todo o sistema está em um plano horizontal, determine a diferença de carga entre as seções de entrada e a saída. Despreze as perdas singulares. Dados: QAB = 0,28 m3/s ; f = 0,024 ; QjBC = 0 ; LAB = 1500 m QAB 1500 m 18" C D 3000 m 27" B 18" 3000 m a) Determinação da perda de carga no trecho AB 5 2.. 0827,0 D QLf H HAB = (f . L) Q^2/D^5 = 0,0827 . 0,024 . 1500 . 0,28^2/0,68^5 HAB = 1,605 m b) Determinação das vazões a montante em cada ramo do trecho em paralelo 5 2.. 0827,0 D QLf H DHBC = DHBD 0,0827 . f . L QfBC^2/D^5 = 0,0827 . f . L QfBD^2/D^5 QfBC = QfBD Relações: 1) QfBC = QfBD QmBC/ 3 = (QmBD + QjBD)/2 2) QjBD = QmBD/2 3) QAB = 0,28 = QmBC + QmBD QmBC/ 3 = (QmBD + QmBD/2)/2 0,28 – QmBD = 3 (3/2 . QmBD)/2 0,28 – QmBD = 3 . 3/4 . QmBD QmBD = 0,12 m3/s QAB = 0,28 = QmBC + QmBD 0,28 = QmBC + 0,120 QmBC = 0,16 m3/s c) Determinação das vazões fictícias QfBC e QfBD QfBC = QmBC/ 3 = 0,16 / 3 = 0,092 m3/s = QfBD (pela relação (1)) d) Determinação da perda de carga no trecho BD 5 2.. 0827,0 D QLf HBD HBD = 0,0827 . 0,024 . 3000 . 0,092^2/0,45^5 HBD = 2,73 m e) Determinação da perda de carga total HAD = HAB + HBD = 1,605 + 2,73 HAD = 4,34 m 33 Pág. 118 numero 4.4 Quando água é bombeada através de uma tubulação A, com uma vazão de 0,20 m3/s, a queda de pressão é de 60 kN/m2, e através de uma tubulação B, com uma vazão de 0,15 m3/s, a queda de pressão é de 50 kN/m2. determine a queda de pressão que ocorre quando 0,17 m3/s de água são bombeados através das duas tubulações, se elas são conectadas a0 em série, b) em paralelo. Neste último, caso calcule as vazões em cada tubulação. Use a fórmula de Darcy-Weisbach. Dados: pA = 60 kN/m2 = 60/9,8 pA/ = 6,12 m e QA = 0,20 m3/s pB = 50 kN/m2 = 50/9,8 pB/ = 5,10 m e QB = 0,15 m3/s 1ºCaso: TUBULAÇÃO EM SÉRIE Q = QA = QB e H = HA + HB a) Determinação das relações entre os parâmetros das tubulações 5 2.. 0827,0 D QLf H HA = 0,0827 fA . LA . 0,20^2/DA^5 = 6,12 m fA . LA/DA^5 = 1850,80 m HB = 0,0827 fB . LB . 0,20^2/DB^5 = 5,10 m fB . LB/DB^5 = 2741,93 m b) Determinação da perda de carga total da tubulação em série 5 2.. 0827,0 D QLf H H = 0,0827 (fA.LA.QA^2/DA^5 + fB.LB.QB^2/DB^5) = H = 0,0827 (1850,8 + 2741,93) . 0,17^2 = 10,98 m ou H = 10,98 . 9800 = 107,57 kN/m2 2ºCaso: TUBULAÇÃO EM PARALELO Q = QA + QB e DH = DHA = DHB c) Determinação das relações entre os parâmetros das tubulações ii i EE E Lf D Lf D .. 55 (DE^5/fE.LE)^1/2 = (1/1850,8)^1/2 + (1/2741,93)^1/2 = 0,0232 + 0,0191= [(DE^5/fE.LE)^1/2]^2 = 0,0423^2 (DE^5/fE.LE) = 0,00179 d) Determinação da perda de carga total 5 2.. 0827,0 D QLf H H = 0,0827 . (1/0,00179) . 0,17^2 H = 1,336 m ou H = 1,336 . 9800 = 13,09 kN/m2 e) Determinação das vazões em cada trecho em paralelo 5 2.. 0827,0 D QLf H Trecho A HA = 0,0827 . (fA.LA/DA^5) . QA^2 = 6,12 = 0,0827 . (1850,8) . QA^2 QA = 0,0934 m3/s Trecho B HB = 0,0827 . (fB.LB/DB^5) . QB^2 = 5,10 = 0,0827 . (2741,93) . QB^2 QB = 0,0767 m3/s 34 Pág. 118 numero 4.5 No sistema mostrado da figura, do ponto A é derivada uma vazão QA = 35 l/s e em B, é descarregada na atmosfera QB = 50 l/s. Dados: L1 = 300 m, D1 = 225 mm, f1 = 0,020, L2 = 150 m, D2 = 125 mm, f2 = 0,028, L3 = 250 m, D3 = 150 mm, f3 = 0,022, L4 = 100 m, D4 = 175 mm, f4 = 0,030. Calcular: a) o valor de H para satisfazer as condições anteriores; b) a cota piezométrica no ponto A. Despreze as perdas localizadas e a carga cinética. L1, D1 A L3, D3 L2, D2 L4, D4 B QB H QA a) Det. do comprimento equivalente do trecho em paralelo (2 e 3) ii i EE E Lf D Lf D .. 55 [0,225^5/(0,020.LA)]^1/2=[0,125^5/(150.0,028)]^1/2+[0,150^5/(250.0,022)]^1/2 [0,225^5/(0,020.LA)]^1/2 = 0,002695 + 0,003716 = 0,006411 LA = [0,225^5/(0,020 . 0,006411^2)] LA = 701,43 m b) Det. do comprimento equivalente do trecho em série (1 e 4) f1.L1/D1^5 = f4.L4/D4^5 0,020.L/0,225^5 = 0,030.100/0,175^5 L = 527 m c) Determinação da perda de carga H = H0A + HAB H0A = 0,0827 . f . L . Q^2/D^5 H0A = 0,0827 . 0,020 . 300 (0,035+0,050)^2/0,225^5 H0A = 6,22 m HAB = 0,0827 . f (LA + L) QB^2/D^5 HAB = 0,0827 . 0,020 (701,435 + 527) . 0,050^2/0,225^5 HAB = 8,80 m DH (total) = 6,22 + 8,80 = 15,0 m d) Determinação da cota piezométrica no ponto A CPA = (pA/ + ZA) + HAB CPA = 0 + 0 +8,80 CPA = 8,80 m 35 Pág. 119 numero 4.6 Uma localidade é abastecida de água a partir dos reservatórios C e D, do sistema de adutoras mostrado na figura. As máximas vazões nas adutoras CA e DA são de 8 l/s e 12 l/s, respectivamente. Determine: a) os diâmetros dos trechos CA e DA, para vazão máxima de 20,0 l/s na extremidade B do ramal AB, de diâmetro igual a 0,20 m, sendo a carga de pressão disponível em B igual a 30 mH2O; b) a vazão que afluiria de cada reservatório ao se produzir uma ruptura na extremidade B. Todas as tubulações são de ferro fundido novo, C = 130. Despreze as cargas cinéticas nas tubulações.240,2 200 C D 172 5 m D = 0,20 m 1803 m 509 m A 159,2 B a) Determinação da cota piezométrica em A (CPA) CPA = CPB + HAB = (pB/ + ZB) + HAB CPA = 30 + 159,20 + (10,65 . 0,020^1,85 . 1803)/(130^1,85 . 0,20^4,87) CPA = 30 + 159,20 + 4,30 CPA = 193,50 m b) Determinação do diâmetro do trecho CA (DCA) CPA = CPC - HCA 193,5 = 200 – (10,65 . 0,008^1,85 . 509)/(130^1,85 . DCA^4,87) DCA = 0,10 m c) Determinação do diâmetro do trecho DA (DDA) CPA = CPD - HDA 193,5 = 240,20 – (10,65 . 0,012^1,85 . 1725)/(130^1,85 . DDA^4,87) DDA = 0,10 m Determinação das vazões nos trechos CA e DA para ocorrer um rompimento em B ( pB/ = patm/ = 0) d) Determinação da cota piezométrica em A CPA = CPB + HAB = (pB/ + ZB) + HAB CPA = 0 + 159,20 + (10,65 . (QCA + QDA)^1,85.1803)/(130^1,85. 0,20^4,87) CPA = 0 + 159,2 + 5.977,70 . (QCA + QDA)^1,85 (I) e) Determinação da cota piezométrica em C CPC = CPA + HCA = CPA + (10,65 . QCA^1,85.509)/(130^1,85. 0,20^4,87) CPC = CPA + 49.348,8,30.QCA^1,85 (II) f) Determinação da cota piezométrica em D CPD = CPA + HDA = CPA + (10,65 . QDA^1,85.1725)/(130^1,85. 0,20^4,87) CPD = CPA + 167.241,30.QDA^1,85 (III) g) RELAÇÕES ENTRE AS EQUAÇÕES II E III CPA = CPA CPC - HCA = CPD - HDA CPD – CPC = HDA - HCA (240,2–200)=10,65.(1725.QDA^1,85–509.QCA^1,85)/(130^1,85. 0,10^4,87) 40,2 .130^1,85 . 0,10^4,87/10,65 = 1725. QDA^1,85 – 509. QCA^1,85 0,415 = 1725.QDA^1,85 – 509.QCA^1,85 h) Explicitando QCA QCA^1,85 = 3,389.QDA^1,85 – 0,00081 36 Pág. 119 numero 4.6 (continuação) i) Utilizando todas as equações para resolver o sistema para QDA CPA = 159,2 + 5.977,7 . [(3,389.Q^1,85 – 0,00081)^(1/1,85) + QDA]^(1,85) Como CPD = CPA + 16.241,3 . QDA^1,85 = 240,2 CPA = 240,2 – 16.241,3 . QDA^1,85 Como CPA = CPA 240,2 – 16.241,3. QDA^1,85 = 159,2 + 5.977,70 . [(3,389.QDA^1,85 – 0,00081)^(1/1,85) + QDA]^1,85 81 – 5.977,70 . [(3,389.QDA^1,85 – 0,00081)^0,54 + QDA]^0,54 = 167.241,3.QDA^1,85 Solving QDA = 0,015 m3/s ou 15 litros/s j) Determinação de QCA QCA = (3,389 . 0,015^1,85 – 0,000815)^0,54 QCA = 0,0184 m3/s ou 18 litros/s 37 Pág. 119 numero 4.7 O sistema de distribuição de água mostrado na figura tem todas as tubulações do mesmo material. A vazão total que sai do reservatório I é de 20 l/s. Entre os pontos B e C, existe uma distribuição em marcha com vazão por metro linear uniforme e igual a q = 0,01 litros/(s.m). Assumindo um fator de atrito constante para todas as tubulações f = 0,020 e desprezando as perdas localizadas e a carga cinética, determine: a) a cota piezométrica no ponto B; b) a carga de pressão disponível no ponto C, se a cota geométrica deste ponto é de 576,00 m; c) a vazão na tubulação de 4” de diâmetro. 580,44 590,0 A D 6" 750 m 4" 800 m6" 576,0 B 500 m I C II 6" 1000 m a) Det. do comprimento equivalente do trecho em paralelo ii i EE E Lf D Lf D .. 55 [0,15^5/(f . LE)]^1/2=[0,10^5/(f . 800)]^1/2+[0,15^5/(f . 750]^1/2 LE = 410,70m b) Determinação da cota piezométrica em B (CPB) CPB = CPA - HAB = 5 2.. 0827,0 D QLf H = 0,0827 . 0,020 . 410,70. 0,020^2/0,15^5 = 3,58 m CPB = CPA - HAB = 590 – 3,58 CPB = 586,42 m 580,44 590,0 A D 6" 410,70 m 6" 576,0 B 500 m I C II 6" 1000 m c) Determinação da vazão fictícia no trecho BC Qj = Qm – q . L = 20 – 0,010 . 1000 = 10 litros/(s.m) Qf = (Qm + Qj)/2 = (0,020 + 0,010)/2 Qf = 0,015 m3/(s.m) ou 15 litros/(s.m) d) Determinação da cota piezométrica em C (CPC) CPC = CPB - HBC = 5 2.. 0827,0 D QLf H HBC = 0,0827 . 0,020 . 1000. 0,015^2/0,15^5 = 4,90 m CPC = CPB - HBC = 586,42 – 4,90 CPC = 581,52 m e) Determinação da carga de pressão no ponto C CPC = (pC/ + ZC) pC/ = CPC - ZC = 581,52 – 576 pC/ = 5,52 m f) Determinação da vazão na tubulação de 4” 5 2.. 0827,0 D QLf H HAB = 0,0827 . 0,020 . 800. Q4”^2/0,10^5 = 3,58 m Q4” = 0,00520 m3/s ou Q4” = 5,20 litros/s 38 Pág. 120 numero 4.8 Três reservatórios A, B e C são conectados por três tubulações que se juntam no ponto J. O nível do reservatório B está 20 m acima do nível de C e o nível de A está 40 m acima de B. Uma válvula de controle de vazão é instalada na tubulação AJ, imediatamente a montante de J. A equação de resistência de todas as tubulações e da válvula é dada por, H (m) = rQ2, em que r é o coeficiente de resistência e Q, a vazão em m3/s. Os valores de r para as três tubulações são: rAJ = 150, rBJ = 200 e rCJ = 300. Determine o valor do coeficiente r de resistência da válvula Hv (m) = rQ2 para que a vazão que chega ao reservatório C seja o dobro da que chega ao reservatório B. 0 C 60 A J válvula 20 B 40 20 0 H = r . Q^2 a) Relações entre as vazões QAJ = QJB + QJC = QJB + 2.QJB QAJ = 3.QJB b) Determinação da energia específica entre A e J HA = HJ + HAJ pA/ + ZA + VA^2/2g = pJ/ + ZJ + VJ^2/2g + HAJdist + HAJvalv 60 + 0 + 0 = (CPJ + VJ^2/2g) + 150 QAJ^2 + r . QAJ^2 EJ c) Determinação da energia específica entre B e J HJ = HB + HJB pJ/ + ZJ + VJ^2/2g = pB/ + ZB + VB^2/2g + HJBdist CPJ + VJ^2/2g = 0 + 20 + 0 + 200 . QBJ^2 EJ = 20 + 200 . QBJ^2 d) Determinação da energia específica entre C e J HJ = HC + HJC pJ/ + ZJ + VJ^2/2g = pC/ + ZC + VC^2/2g + HJCdist CPJ + VJ^2/2g = 0 + HJCdist EJ = HJCdist e) Determinação da vazão QJB HJC = EJ rCJ . QJC^2 = HJC 300 . QJC^2 = 20 + 200 . QBJ^2 300 . (2 . QJB)^2 = 20 + 200 . QBJ^2 (1200 – 200) . QJB^2 = 20 QJB = (20/100)^0,5 QJB = 0,14 m3/s f) Determinação da vazão QAJ QAJ = 3 . QJB = 3 . 0,14 QAJ = 0,42 m3/s EJ = 20 + 200 . 0,14^2 EJ = 23,92 m g) Determinação da constante r Como: 60 = EJ + 150 . QAJ^2 + r . QAJ^2 60 = 23,92 + 150 . 0,42^2 + r . 0,42^2 60 = 23,92 + 26,42 + 0,1764 . r r = 9,620 / 0,1764 r = 54,53 39 Pág. 120 numero 4.9 O esquema de adutoras mostrado na figura faz parte de um sistema de distribuição de água em uma cidade, cuja rede se inicia no ponto B. Quando a carga de pressão disponível no ponto B for de 20,0 mH2O, determine a vazão no trecho AB e verifique se o reservatório II é abastecido ou abastecedor. Nessa situação, qual a vazão QB que está indo para a rede de distribuição? A partir de qual valor da carga de pressão em B a rede é abastecida somente pelo reservatório I? Material das tubulações: aço rebitado novo (C = 110). Despreze as perdas localizadas e as cargas cinéticas e utilize a fórmula de Hazen-Williams. 735,0 C 754,0 A 720,0 m B QB 8" 1050 m 6" 650 m a) Determinação da vazão no trecho AB (QAB) CPA = 754 m ; CPC = 735 m CPB = ZB + pB/ = 720 + 20 = 740 m CPA = CPB + HAB 754 = 740 + (10,65 . QAB^1,85 . 1050)/(110^1,85 . 0,20^4,87) QAB = 0,0429 m3/s ou QAB = 42,90 litros/s b) Situação do Reservatório 2 Como CPC = 735m < CPB = 740m então o Reservatório 1 abastece o Reservatório 2. c) Determinaçãoda vazão no trecho BC (QBC) CPB = CPC + HBC 740 = 735 + (10,65 . QBC^1,85 . 650)/(110^1,85 . 0,15^4,87) QBC = 0,01494 m3/s ou QBC = 14,94 litros/s d) Determinação da vazão em B (QB) QAB = QB + QBC QB = QAB – QBC = 42,90 – 14,95 QB = 27,95 litros/s e) A partir de qual pressão em B o R2 passa também a abastecer o ponto B. CPB ≤ CPC ZB + pB/ ≤ ZC + pC/ 720 + pB/ ≤ 735 pB/ ≤ 735 – 720 pB/ ≤ 15 m 40 Pág. 120 numero 4.10 No sistema de abastecimento d’água mostrada na figura, todas as tubulações têm fator de atrito f = 0,021 e, no ponto B, há uma derivação de 5,0 l/s. Desprezando as perdas de carga localizadas e as cargas cinéticas, determine a carga de pressão disponível no ponto A e as vazões nos trechos em paralelo. 810,5 C 30 l/s 81 0 m 8" 6"795,4 B I A 8" 79 0 m 5 l/s 1000 m 810,5 C 30 l/s 36 0,1 3 m 8"795,4 B I A 8" 5 l/s 1000 m a) Determinação do comprimento equivalente no trecho em paralelo Tubulação em paralelo ii i EE E Lf D Lf D .. 55 (8^5/Leq)^0,5 = (8^5/790)^0,5 + (6^5/810)^0,5 Leq = 360,13 m b) Determinação da pressão no ponto A (pA/) CPA = CPC + HAJ pA/ + ZA = pC/ + ZC + HACdist (= 0,0827 f LQ^2/D^5) (4,88 m) pA/ + 795,4 = 810,5 + 0,0827 . 0,021 . 1000 . 0,030^2/0,20^5 + (1,22 m) 0,0827 . 0,021 . 360,13 . 0,025^2/0,20^5 pA/ = 21,20 m c) Determinação das vazões dos trechos em paralelo 5 2.. 0827,0 D QLf H 1,22 = 0,0827 . 0,021 . 790 Q8”^2/0,20^5 Q8” = 0,01687 m3/s ou Q8” = 16,87 litros/s 1,22 = 0,0827 . 0,021 . 790 Q6”^2/0,15^5 Q8” = 0,00813 m3/s ou Q8” = 8,13 litros/s d) Determinação da cota piezométrica no ponto A (CPA) CPA – CPC = DHAC = 0,0827 . 0,021 . 1360,13 0,030^2/0,20^5 CPA – 810,5 = 6,64 CPA = 817,14 m e) Determinação da cota piezométrica no ponto B (CPB) CPA – CPB = DHAB = 0,0827 . 0,021 . 1000 . 0,030^2/0,20^5 817,14 – CPB = 4,88 CPB = 812,14 m 41 Pág. 121 numero 4.11 No sistema adutor mostrado na figura, todas as tubulações são de aço soldado com algum uso, coeficiente de rugosidade da equação de Hazen-Williams C = 120. O traçado impõe a passagem da tubulação pelo ponto B de cota geométrica 514,40 m. O diâmetro do trecho CD é de 6” e a vazão descarregada pelo reservatório superior é de 26 l/s. Dimensione os outros trechos, sujeito a: a) a carga de pressão mínima no sistema deve ser de 2,0 mH20; b) as vazões que chegam aos reservatórios E e D devem ser iguais. Despreze as perdas de carga localizadas e as cargas cinéticas. Dados: C = 120 ; ZB = 514,40 m ; (p/)min = 2 m ; QAB = QBC = QCD + QCE = 26 l/s QCD = QCE = 26/2 = 13 l/s 495 E 520 A C 360 m B 507,2 D 26 l/s 800 m 450 m 6" 20 0 m a) Determinação do diâmetro do trecho AB (DAB) CPA = CPB + HAB 520 = (514,2 + 2,0) + HAB HAB = 3,60 m J = HAB/L = 3,60/800 = 10,65 . 0,026^1,85/(120^1,85 . DAB^4,87) DAB = 0,20 m b) Determinação da cota piezométrica em B (CPB) CPB= pB/ + ZB = 514,4 + 2,0 CPB = 516,40 m c) Determinação da cota piezométrica em C (CPC) CPD = CPC + HCD CPC = CPD – HCD = CPC = 507,2 – (10,65 . 0,013^1,85 . 200/(120^1,85 . 0,15^4,87) CPC = 507,20 – 1,01 CPC = 506,19 m d) Determinação do diâmetro do trecho CD (DBC) CPB = CPC + HBC HBC = CPB – CPC = 516,40 – 506,19 HBC = 10,21 m = 10,65 . 0,026^1,85 . 450/(120^1,85 . DBC^4,87) DBC = 0,15 m e) Determinação do diâmetro do trecho CE (DCE) CPC = CPE + DHCE HCE = CPC – CPE = 506,19 – 495 HBC = 11,19 m = 10,65 . 0,013^1,85 . 360/(120^1,85 . DCE^4,87) DCE = 0,10 m 42 Pág. 121 numero 4.12 A diferença de nível entre dois reservatórios conectados por um sifão é 7,5m. O diâmetro do sifão é 0,30 m, seu comprimento, 750 m e coeficiente de atrito f = 0,026. Se ar é liberado da água quando a carga pressão absoluta é menor que 1,2 mH2O, qual deve ser o máximo comprimento do tramo ascendente do sifão para que ele escoe a seção plena, sem quebra na coluna de líquido, se o ponto mais alto está 5,4 m acima do nível do reservatório superior. Neste caso, qual é a vazão. Pressão atmosférica local igual a 92,65 kN/m2. Dados: D = 0,30 m h = 5,40 m f = 0,026 DZ = 7,50 m L = 750 m pab/g =< 1,20 m pc/g patm/g = 92,65 . 10^3 / 9,8 . 10^3 = 9,45 m = pA/g D B C Z h A a) Determinação da vazão 5 2.. 0827,0 D QLf H = 0,0827 . 0,026 . 750 .Q^2/0,30^5 z = 7,5 = 0,0827 . 0,026 . 750 .Q^2/0,30^5 Q = 0,106 m3/s b) Determinação da velocidade na tubulação v = 4Q/(3,14 . D^2) = 4 . 0,106/ 3,14 . 0,30^2 v = 1,50 m/s c) Determinação do comprimento LBC HA = HC + HAC pA/ + ZA + VA^2/2g = pC/ + ZC + VC^2/2g + HBC 9,45 + 7,5 + 0 = 1,20 +(7,5 + 5,4) + 1,5^2/19,6 + 0,0827.0,026.LBC.0,106^2/0,3^5 9,45 = 1,20 + 5,40 + 0,115 + 0,0099422.LBC LBC = 2,735/0,0099422 = LBC = 275 m Adicional d) Determinação das cotas piezométricas CPA = 9,45 + 7,5 = 16,95 m CPC = 1,20 + (7,5 + 5,40) = 14,10 m 43 Pág. 121 numero 4.13 Dois reservatórios têm uma diferença de nível igual a 15 m e são conectados por uma tubulação ABC, na qual o ponto mais alto B está 2 m abaixo do nível d’água do reservatório superior A. O trecho AB tem diâmetro de 0,20 m e o trecho BC, diâmetro de 0,15 m, e o fator de atrito é o mesmo para os dois trechos. O comprimento total da tubulação é 3000 m. Determine o maior valor do comprimento AB para que a carga de pressão em B não seja maior que 2 mH20 abaixo da pressão atmosférica. C B Z = 15 m h=2 m A y=-2 m DAB = 0 ,20 m DBC = 0,15 m DADOS: Q = ? ; LAB +LBC = 3000 m ; LAB = ? ; pB/ = -2 m (abaixo da pressão atmosférica) a) Determinação da perda de carga CPA = CPB + DHAB 2 = -2 + DHAB DHAB = 4 m g v D L fH 2 2 DHAB = f.(LAB/DAB).v^2/2g = 4 (1) DHBC = f.(LBC/DBC).v^2/2g = 11 (2) E ainda Q = 3,14 . 0,20^2/4 . vAB = 3,14.0,15^2/4 . vBC vAB = (0,15/0,20).vBC vAB = 0,562 . vBC - Dividindo (1) por (2), tem-se: DHAB/DHBC = (LAB.DBC/LBC.DAB) . vAB^2/vBC^2 4/11 = (LAB/(3000-LAB)).0,15/0,20 . (0,562.vBC)^2/vBC^2 0,364 = LAB/(3000-LAB) . 0,75 . 0,316 LAB/(3000-LAB) = 1,537 2,537.LAB = 4.609,87 LAB = 1.817,05 m 44 Pág. 121 numero 4.14 Um tanque cilíndrico aberto de 1,0 m de diâmetro está sendo esvaziado por um tubo de 50 mm de diâmetro e 4,0 m de comprimento, com entrada em aresta viva, K = 0,5, para o qual f = 0,025, e descarregando na atmosfera. Determine o tempo necessário para que a diferença entre o nível d’água no tanque e o nível da saída do tubo caia de 2,0 m para 1,0 m. t = 0 k = 0,5 D = 0,05 m L = 4 mf = 0,025 D=1m Z = 1 m a = 2 m a) Determinação das áreas Reservatório: AR = 3,14.DR^2/4 = 3,14.1^2/4 = 0,785 m2 Tubulação:AT = 3,14.DT^2/4 = 3,14.0,05^2/4 = 0,002 m2 b) Perda de carga localizada e distribuída )/.( 2 DLfk g = (19,6/(1+0,5+0,025.4/0,05))^0,5 = 2,366 c) Tempo necessário para o abaixamento de z = 2m a 1 m )/1.(. ][2 21 1 AAA HHoA t t t = 2.0,785.((2)^0,5 – (1)^0,5)/(2,366.0,002) = t = 331,723 . 0,414 t = 137 ~ 140 segundos 45 Pág. 121 numero 4.15 Dois reservatórios prismáticos, um de área igual a 7,4 m2 e outro de área igual a 3,7 m2, estão ligados por uma tubulação de 125 m de comprimento e 50 mm de diâmetro, com fator de atrito f = 0,030. Determine o tempo necessário para que um volume de 2,3 m3 de água seja transferido do tanque maior para o menor, se a diferença de nível inicial entre eles é de 1,5 m. Coeficientes de perda de carga, na entrada K = 0,5 e na saída K = 1,0. t = 0 k = 0,5 D = 0,05 m L = 125 mf = 0,030 Ho = 1,50 m k = 1,0 DADOS: Ho = 1,50m D = 0,050 m f = 0,030 A1 = 7,40 m2 k = 0,5 + 1,0 = 1,5 A2 = 3,7 m2 L = 125 m a) Determinação dos parâmetros )/.( 2 DLfk g = (19,6/(1,5 + 0,030*125/0,05))^0,5 = 0,506 At = 3,14*D^2/4 = 3,14*0,05^2/4 = 0,0019625 m2 H = Ho – volume/Áreas = 1,5 – 2,3/7,4 – 2,3/3,7 = 0,567 m b) Tempo necessário para o abaixamento de z = 2m a 1 m )/1.(. ][2 21 1 AAA HHoA t t )7,3/4,71.(0019625,0.506,0 ]567,05,1[4,7*2 t t = 6,98/0,00297 t = 2343,6 segundos t ~ 39 minutos 46 Pág. 122 numero 4.16 Um reservatório alimenta uma tubulação de 200 mm de diâmetro e 300 m de comprimento, a qual se divide em duas tubulações de 150 mm de diâmetro e 150 m de comprimento, como o da figura abaixo. Ambos os trechos estão totalmente abertos para a atmosfera nas suas extremidades. O trecho BD possui saídas uniformemente distribuídas ao longo de seu comprimento, de maneira que metade da água que entra é descarregada ao longo de seu comprimento. As extremidades dos dois trechos estão na mesma cota geométrica e 15 m abaixo do nível d’água do reservatório. Calcule a vazão em cada trecho adotando f = 0,024, desprezando as perdas localizadas e a carga cinética nas tubulações. Resolva o problema de duas maneiras: primeiro, usando no trecho BD o conceito de vazão fictícia e, segundo determinando a perda de carga distribuída em um elemento de comprimento dL e depois fazendo a integração de 0 a L (de B até D): Z = 15 m A B DC Dados: DAB = 0,20 m ; DBC = DBD = 0,15 m ; f = 0,024 LAB = 300 m ; LBD = LBC = 150 m a) Determinação das relações entre as vazões nos trechos QAB = QBC + QBDfictícia DHBD = DHBC 0,0827.f.L.Qf^2/D^5 = 0,0827.f.L.QBC^2/D^5 Qf = QBC QBDfic = QBC = (Qm + Qj)/2 = (Qm + Qm/2)/2 Qf = QBC = ¾ . Qm e como: QAB = QBC + Qm = QBC + 4/3.QBC QAB = 7/3 . QBC b) Determinação da vazão no trecho AB (QAB) DHAB + DHBC = 15 m 0,0827.0,024[300QAB^2/0,2^5 + 150(3/7.QAB)^2/0,15^5] = 15 937.500.QAB^2 + 362.811,79.QAB^2 = 15/(0,0827.0,024) QAB = (7.557.436/1.300.311,79)^0,5 QAB = 0,076 m3/s c) Determinação da vazão no trecho BC (QBC) QAB = 7/3 . QBC QBC = 3/7 . 0,076 QBC = 0,033 m3/s d) Determinação da vazão no trecho BD (QBD) Qf = QBD = 4/3 . QBC = 4/3 . 0,033 QBD = 0,043 m3//s 47 Pág. 122 numero 4.17 De uma represa mantida em nível constante sai uma tubulação de ferro fundido novo, de 200 mm de diâmetro e 500 m de comprimento, que termina no fundo de um reservatório prismático de 10 m2 de área e 5 m de altura, conforme a figura. Estando inicialmente vazio e reservatório, abre-se o registro colocado em A. Calcular o tempo necessário para o enchimento completo do reservatório o fator de atrito da tubulação seja constante, com valor médio f = 0,020. Resolva o problema de duas maneiras distintas: a) utilizando a Equação 4.39 observando que, no caso, tem-se A1>>>A2 = 10 m2. b) Utilizando a Equação 2.42 e observando que, pela equação da continuidade, em um tempo qualquer t, a vazão que entra no reservatório é dada por Q = - A dh/dt, em que h é uma ordenada marcada positiva de cima para baixo a partir da cota 5,0 m e A a área do reservatório. Despreze as perdas de carga localizadas na tubulação. 5,0 0,0 A 5,0 L = 500 m D = 200 mm a) Determinação dos parâmetros )/.( 2 DLfk g = (19,6/(0+0,020.500/0,20))^0,5 = 0,626 A = 3,14.D^2/4 = 3,14 . 0,20^2/4 = 0,0314 m2 b) Determinação do tempo de enchimento do reservatório )/1.(. [2 21 1 AAA HHoA t t ; A1 >>>A2 = 10 m2 t = 2.10.((5)^0,5 – (0)^0,5)/((0,626.0,0314.(1+0)) = 2274,80 s t = 37,90 minutos ou t = 38 minutos 48 CAPÍTULO 5 CAPÍTULO 5 49 Pág. 131 exemplo 5.1 O projeto de um sistema de elevatório para abastecimento urbano de água deverá ser feito a partir dos seguintes dados: a) vazão necessária Q = 80 l/s; b) altura geométrica a ser vencida Hg = 48 m; c) comprimento da linha de recalque L = 880 m; d) material da tubulação ferro fundido classe K7, rugosidade = 0,4 mm; e) número de horas de funcionamento diário T = 16 h; f) número de dias de funcionamento no ano N = 365; g) taxa de interesse e amortização do capital 12% a.a; h) rendimento adotado para a bomba = 70%; i) rendimento adotado para o motor = 85%; j) preço do quilowatt-hora A = R$ 0,031. Uma pesquisa de preço de tubos, por unidade de comprimento, para 150 < D < 500 mm levou à seguinte relação entre diâmetro e custo: Custo (R$/m) = 0,042 D(mm)^1,4. Determine o diâmetro econômico de recalque. e (mm) = 0,4 N = 365 Q (l/s) = 80 i (%) = 12 Hg (m)= 48 n = 0,7 L rec (m) = 880 nm = 0,85 T (h) = 16 preço (kwh)= 0,031 (A) (B) © (D) (E) (F) (G) Diâmetro Rey J H=Hg+JL Custo anual Custo Custo (mm) (m/m) (m) bombeamento anual tub total 150 679.081,12 0,1790 205,50 49.022,22 4.936,75 53.958,97 200 509.310,84 0,0396 82,84 19.761,82 7.385,08 27.146,90 250 407.448,67 0,0124 58,87 14.042,80 10.093,21 24.136,01 300 339.540,56 0,0048 52,21 12.455,11 13.028,16 25.483,27 350 291.034,77 0,0022 49,90 11.902,69 16.166,22 28.068,90 400 254.655,42 0,0011 48,95 11.677,56 19.489,34 31.166,90 450 226.360,37 0,0006 48,52 11.574,42 22.983,21 34.557,63 500 203.724,34 0,0003 48,30 11.522,70 26.636,14 38.158,83 y = -0,0041x3 + 4,6802x2 - 1648,5x + 207628 R2 = 0,927 20.000,00 30.000,00 40.000,00 50.000,00 60.000,00 150 200 250 300 350 400 450 500 D (mm) Cu sto to tal an ua l (R $) Conclusão: As colunas G e A da tabela anterior foram postas em forma gráfica, indicando que o valor mínimo da soma (custo total), coluna E + coluna F, ocorre para um diâmetro de 250 mm que deverá ser adotado para o diâmetro econômico das instalações de recalque. 50Pág. 138 exemplo 5.2 Uma bomba KSB-MEGANORM, modelo 32-160, com rotor de diâmetro igual a 162 mm (R=81 mm), na rotação de 1750 rpm, trabalha no ponto A recalcando uma vazão Q = 10 m3/h com altura de elevação H = 10,5 m (ver figura). a) Classifique o tipo da bomba. b) Trace a curva característica adimensional da bomba, f). c) Qual o ponto de funcionamento (homólogo de A) de uma bomba geometricamente semelhante a esta, com uma rotação igual e diâmetro do rotor igual a 172 mm. Dados: D = 162 mm; n = 0,525 ; Q = 14 m3/h; H = 9,25 m; a) Determinação do tipo da bomba O tipo da bomba pode ser calculado pela determinação da rotação específica Pág. 142 exemplo 5.3 Uma bomba centrifuga, com rotação igual 1750 rpm e curva característica dada pela tabela a seguir, está conectada a um sistema de elevação de água que consta de duas tubulações em paralelo e dois reservatórios. Uma tubulação de 0,10 m de diâmetro, comprimento de 360 m e fator de atrito f = 0,015 está ligada ao reservatório com nível d’água na cota 800,00 m, e a outra, de 0,15 m de diâmetro, comprimento de 900 m e fator de atrito f = 0,030, está ligada ao reservatório com nível d’água na cota 810,0 m. O reservatório inferior tem nível d’água na cota 780,000 m. Assumindo que os fatores de atrito sejam constantes, independentes da vazão, determine: a) o ponto de funcionamento do sistema; b) as vazões em cada tubulação da associação; c) a potência necessária à bomba. Pág. 146 exemplo 5.4 As características de uma bomba centrífuga, em uma certa rotação constante, são dadas na tabela abaixo: A bomba é usada para elevar água vencendo uma altura geométrica de 6,5 m, por meio de uma tubulação de 0,10 m de diâmetro, 65 m de comprimento e fator de atrito f = 0,020. a) Determine a vazão recalcada e a potência consumida pela bomba; b) Sendo necessário aumentar a vazão pela adição de uma segunda bomba idêntica à outra, investigue se a nova bomba deve ser instalada em série ou em paralelo com a bomba original. Justifique a resposta pela determinação do acréscimo de vazão e a potência consumida por ambas as bombas nas associações. André Barcellos Ferreira – andrepoetta@hotmail.com 1 Universidade Federal do Espírito Santo HIDRÁULICA BÁSICA – 4ª edição EXERCÍCIOS RESOLVIDOS Exercícios propostos do capítulo 2: 2.7, 2.10, 2.14, 2.16, 2.20, 2.21, 2.23, 2.34, 2.35, 2.36. (pg. 1) Exercícios propostos do capítulo 3: 3.1, 3.7, 3.8, 3.10, 3.13. (pg. 7) Exercícios propostos do capítulo 4: 4.1, 4.4, 4.7 e 4.9. (pg. 11) Exercícios propostos do capítulo 5: 5.1, 5.2 5.4, 5.6, 5.8, 5.14. (pg. 16) Exercícios propostos do capítulo 6: 6.1, 6.2, 6.6. (pg. 22) Exercícios propostos do capítulo 8: 8.1, 8.2, 8.3, 84, 8.5, 8.6, 8.8, 8.10, 8.19, 8.20. (pg. 27) Exercícios propostos do capítulo 9: 9.5, 9.6, 9.8. (pg. 33) Exercícios propostos do capítulo 12: 12.7, 12.9, 12.13, 12.18. (pg. 35) 2.7 Água escoa em um tubo liso, εεεε = 0,0 mm, com um número de Reynolds igual a 106. Depois de vários anos de uso, observa-se que a metade da vazão original produz a mesma perda de carga original. Estime o valor da rugosidade relativa ao tubo deteriorado.1 J → perda de carga onde f → fator de atrito V → velocidade média Na situação final, J0(Q) = J(Q/2). Portanto: ( ) ( )2 2 2 20 0/ / 2 2 2 4 Q A Q Af f f Q f Q D g D g A A ⋅ ⋅ ⋅ = ⋅ ⇔ = ( ) ( ) 2 2 5,4 5,4 6 0,9 6 0,9 0,25 1 5,74 5,74log 2log 3,710 10 5,74 5,74log log 3,7 10 10 D D ε ε ∴ = ⇔ = + ⇔ + 3 5 5,4 5,4 5,4 5,74 5,74 100 5,74 2,262 10100 (1 100) 8,370 10 3,7 3,7 27,02710 10 10D D D ε ε ε − − − ⋅ ⇔ = + ⇔ = − ⇔ = = − ⋅ Resolvendo por um outro método, tem-se: (antes) 2 1 1 4 V DQ pi⋅ ⋅= 2 1 1 1 2 L VH f D g ∆ = (depois) 2 1 1 2 V V= 2 2 2 1 2 1 2 1 2 142 2 L V L VH H f f f f D g D g ∆ = ∆ ⇒ ⋅ ⋅ = ⋅ ⋅ ⇔ = Recentemente, Swamee apresentou uma equação geral para o cálculo do fator de atrito, válida para os escoamentos laminar, turbulento liso, turbulento rugoso e de transmissão, na forma: 0,125168 6 0,9 64 5,74 25009,5 ln Re 3,7 ReRe f y D yy ε − = + + − Pela equação de Swamee, aplicada no tubo liso: 2 0,9 0,25 2 5,74log 3,7 Re f VJ f D g D y ε = = + André Barcellos Ferreira – andrepoetta@hotmail.com 2 Universidade Federal do Espírito Santo ( ) ( ) ( ) 0,125168 65 5 36,4 10 9,5 ln 2,28 10 2,5 10 0,011597f − − − − = ⋅ + ⋅ − ⋅ = Assim: 2 1 24 0,046388f f f= ⇒ = Pela equação do tubo rugoso: 1 12,04log 1,67 2,04log 1,67 20,046338 R D f ε ε = + ⇒ = + ⇔ 4,64298 2,04 log log 2 1,67 1,4573 log log 2 log 1,7584D D D ε ε ε ⇔ = − + ⇔ = − ⇔ = ⇔ 0,0174 D ε = 2.10 Em uma tubulação circular, a medida de velocidade do escoamento, a uma distância de parede igual a 0,5 R, em que R é o raio da seção, é igual a 90% da velocidade na linha central (velocidade máxima). Determine a relação entre a velocidade média V e a velocidade central vmáx, e a rugosidade relativa da tubulação. Sugestão: utilize o resultado do Exemplo 2.2 e as Equações 2.20 e 2.34. Equação 2.20 ⇒ * 2,5lnmáxv V R u y − = Equação 2.34 ⇒ 1 3,712log Df ε = Do Exemplo 2.2, *4,07 0,765máx máxv V u V v= + → = * * * 0,9 2,5ln 1,733 0,1 1,733 0,577 0,5 máx máx máx máx v v R v u u v u R − = = ⇔ = ⇔ = Pela Equação 2.32 * 2,5ln 4,73V R u ε = + , tem-se: 0,765 2,5ln 4,73 ln 3,41 30,30 0,0165 0,577 2 2 2 máx máx v D D D v D ε ε ε ε = + ⇔ = ⇔ = ⇒ = 2.14 Em relação ao esquema de tubulações do exemplo 2.8, a partir de que vazão QB, solicitada pela rede de distribuição de água, o reservatório secundário, de sobras, passa a ser também abastecedor? Para aço soldado novo, C = 130 (Tabela 2.4). Pela Tabela 2.3, determina-se β (β1 = 1,345⋅103) No trecho AB: D1 = 6”, C = 130 e J1 = 1,12 m/100 m → β1 = 1,345⋅103 1,85 3 1,85 1 1 1 1 11,12 1,345 10 0,0216J Q Q Qβ= ∴ = ⋅ ∴ = m3/s No trecho BC: D2 = 4”, C = 130, J2 = 1,12 m/100 m, β2 = 9,686⋅103 1,85 3 1,85 2 2 2 2 21,12 9,686 10 0,00745J Q Q Qβ= ∴ = ⋅ ∴ = m3/s A diferença é consumida na rede: QB = 0,0216 – 0,00745 = 0,01415 m3/s = 14,2 l/s A cota piezométrica em A é CPA = 812,0 m. Em B é a cota menos a perda: CPB = CPA – ∆HAB = 812 – J1L1 = 812 – 0,0112⋅650 = 804,72 m A partir de que vazão QB o reservatório de sobras também é utilizado? André Barcellos Ferreira – andrepoetta@hotmail.com 3 Universidade Federal do Espírito Santo Neste caso, CPB < 800m 1 812 800 0,0185 650 HJ L ∆ − = = = m/m Aço soldado novo: C = 130 (tabela 2.4) D1 = 6”, C = 130, J1 = 1,85 m/100 m, β1 = 1,345⋅103 1,85 3 1,85 1 1 1 1 11,85 1,345 10 0,02836J Q Q Qβ= ∴ = ⋅ ⇔ = m3/s = 28,36 l/s 2 800 800 0 420 J −= = Toda a vazão proveniente do reservatório superior é utilizada no abastecimento na iminência. Para que o reservatório inferior entre em operação, QB > 28,36 l/s. 2.16 Na tubulação da figura 2.10, de diâmetro 0,15 m, a carga de pressão disponível no ponto A vale 25 mH2O. Qual deve ser a vazão para que a carga de pressão disponível no ponto B seja 17 mH2O? A tubulaçãode aço soldado novo (C = 130) está no plano vertical. Carga de pressão em CPA = 25 mH2O. Qual deve ser a vazão para que a carga de pressão em B seja CPB = 17 mH2O? 25AP γ = m, 17BP γ = m, zA = 0, zB = 5 m 2 2 , 2 2 A A B B A B P V P V z z H g gγ γ + + = + + + ∆ vA = vB ⇒ 25 = 17 + 5 +∆H ⇔ ∆H = 3 mH2O Pela tabela 2.3, β = 1,345⋅103 3 0,0191 157,1 HJ L ∆ = = = m/m = 1,91 m/100 m 11 1,851,851,85 3 1,91 28,9 1,345 10 JJ Q Qβ β = ⇒ = = = ⋅ l/s 2.20 Em uma adutora de 150 mm de diâmetro, em aço soldado novo (εεεε = 0,10 mm), enterrada, está ocorrendo um vazamento. Um ensaio de campo para levantamento de vazão e pressão foi feito em dois pontos, A e B, distanciados em 500 m. No ponto A, a cota piezométrica é 657,58 m e a vazão, de 38,88 l/s, e no ponto B, 643, 43 m e 31,81 l/s. A que distância do ponto A deverá estar localizado o vazamento? Repita o cálculo usando a fórmula de Hazen-Williams. D = 150 mm QA = 38,88 l/s QB = 31,81 l/s ε = 0,10 mm CPA = 657, 58 m L = 500 m CPB = 643,43 m Fórmula universal da perda de carga: 2 ; 2 L VH f D g ∆ = 2 ; 2 fVJ Dg = H L J∆ = × • A – C: 3 2 38,88 10 2,20 0,075 A A Q v A pi − ⋅ = = = ⋅ m/s; ƒA = 0,0191; 20,0191 2,20 0,0314 2 2 0,15 9,8 A A A f VJ Dg ⋅ = = = ⋅ ⋅ m/m • B – C: André Barcellos Ferreira – andrepoetta@hotmail.com 4 Universidade Federal do Espírito Santo 3 2 31,81 10 1,80 0,075 B B Q v A pi − ⋅ = = = ⋅ m/s; ƒB = 0,0193; 20,0193 1,80 0,0213 2 2 0,15 9,8 B B B f VJ Dg ⋅ = = = ⋅ ⋅ m/m Pela ideia de que a energia total se mantém constante, e como o escoamento é constante, pode-se usar a equação 2 2 , 2 2 A A B B A B p V p V z z H g gγ γ + + = + + + ∆ onde .n n n p z CP γ + = Colocando os valores do problema, tem-se: 2 22,20 1,80657,58 643,43 657,83 643,60 14,23 2 9,8 2 9,8 H H H+ = + + ∆ ⇔ = + ∆ ⇔ ∆ = ⋅ ⋅ m Sabe-se que a perda de carga total é devida à perda de carga nos pontos A e B. Assim: ( )0,0314 0,0213 500 14,23A B A A B B A AH H H J L J L L L∆ = ∆ + ∆ = + = ⋅ + ⋅ − = ⇔ 3,580,0101 14,23 10,65 354,45 0,0101A A L L⇔ ⋅ = − ⇔ = = m Pela fórmula de Hazen-Williams: J = βQ1,85, βA = βB = 1,345⋅103 JA = 1,345⋅103(38,88⋅10–3)1,85 → JA = 3,309 m/100 m JB = 1,345⋅103(31,81⋅10–3)1,85 → JB = 2,283 m/100 m Portanto: ∆HA + ∆HB = ∆H ⇔ JALA + JBLB = ∆H ⇔ 0,0314LA + 0,02283(500 – LA) = 14,2 ⇔ ⇔ 14,23 500 0,02283 274,37 0,03309 0,02283A L − ⋅= = − m 2.21 Em uma tubulação horizontal de diâmetro igual a 150 mm, de ferro fundido em uso com cimento centrifugado, foi instalada em uma seção A uma mangueira plástica (piezômetro) e o nível d’água na mangueira alcançou a altura de 4,20 m. Em uma seção B, 120 m à jusante de A, o nível d’água em outro piezômetro alcançou a altura de 2,40 m. Determine a vazão. D = 150 mm = 0,15 m C = 130 Tabela 2.3 → β = 1,345⋅103 1,85J Qβ= ⋅ e HJ L ∆ = 1,85 3 4,20 2,40 1,5100 0,0253 120,00 1,345 10 J Q Q− = → = ⇒ = ⋅ m3/s = 25,3 l/s Outro método: D = 150 mm = 0,15 m CPA = 4,20 m CPB = 2,40 m DAB = 120 m VA = VB ⇒ 4,2 2,4 1,8H H= + ∆ ⇔ ∆ = m 1,8 0,015 120 H J L J∆ = ⋅ ⇒ = = 1,85 1,85 4,37 1,85 4,37 1,85 1,85 4,37 0,015 130 0,1510,65 10,65 10,65 Q J C DJ Q C D ⋅ ⋅ ⋅ ⋅ = ⇒ = = 1,85 32,878 10 0,0423Q −⇔ = ⋅ = m3/s = 42,3 l/s 2 2 2 2 2 2 2 2 A A B B A B A B A B P V P V V V z z H CP CP H g g g gγ γ + + = + + + ∆ ⇔ + = + + ∆ André Barcellos Ferreira – andrepoetta@hotmail.com 5 Universidade Federal do Espírito Santo 2.23 A ligação entre dois reservatórios, mantidos em níveis constantes, é feita por duas tubulações em paralelo. A primeira, com 1500 m de comprimento, 300 mm de diâmetro, com fator de atrito f = 0,032, transporta uma vazão de 0,056 m3/s de água. Determine a vazão transportada pela segunda tubulação, com 3000 m de comprimento, 600 mm de diâmetro, e fator de atrito f = 0,024. A perda de carga é a mesma: 1 2 1 1 2 2f fh h J L J L= ⇔ = 2 2 5 8 f QJ g Dpi = ⇒ 2 2 5 2 21 1 2 2 1 2 22 4 2 4 5 1 2 8 8 0,032 600 1500 0,056 0,259 0,024 300 3000 f Q f QL L Q g D g Dpi pi ⋅ ⋅ ⋅ = ⋅ ⇒ = = ⋅ ⋅ m3/s Por outro método: 1. L1 = 1500 m 2. L2 = 3000 m D1 = 300 mm = 0,3 m D2 = 600 mm = 0,6 m f1 = 0,032 f2 = 0,024 Q1 = V1A1 Q2 = ? 2 1 1 0,07074 DA pi ⋅= = m2 2 2 2 0,28274 DA pi ⋅= = 1 1 1 0,7922QV A = = m/s 22 2 2 2 2 2 3,5368QQ V A V Q A = ⋅ ⇔ = = Tubulações em paralelo → ∆H1 = ∆H2 2 2 2 2 2 2 1 1 1 2 2 2 1 1 1 2 2 2 1 2 1 22 2 2 2 f V f L V f L V f L V f L V f L VH J L H L D g D g D g D g D D ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅∆ = ⋅ ⇔ ∆ = = ∴ = ⇔ = ⋅ ⋅ ⋅ ⋅ 2 2 2 20,032 1500 0,7922 0,024 3000 3,5368 0,3 0,6 Q⋅ ⋅ ⋅ ⋅ ⋅ ⇒ = ⇒ 2 2 2 2 0,032 1500 0,7922 0,6 0,25864 0,3 0,024 3000 3,5368 Q ⋅ ⋅ ⋅⇒ = = ⋅ ⋅ ⋅ m3/s = 258,64 l/s 2.34 Uma tubulação de 0,30 m de diâmetro e 3,2 km de comprimento desce, com inclinação constante, de um reservatório cuja superfície está a uma altura de 150 m, para outro reservatório cuja superfície livre está a uma altitude de 120 m, conectando-se aos reservatórios em pontos situados 10 m abaixo de suas respectivas superfícies livres. A vazão através da linha não é satisfatória e instala-se uma bomba na altitude 135 m a fim de produzir o aumento de vazão desejado. Supondo que o fator de atrito da tubulação seja constante e igual a f = 0,020 e que o rendimento da bomba seja 80%, determine: a) a vazão original do sistema por gravidade; b) a potência necessária à bomba para recalcar uma vazão de 0,15 m3/s; c) as cargas de pressão imediatamente antes e depois da bomba, desprezando as perdas de carga localizadas e considerando a carga cinética na adutora; d) desenhe as linhas de energia e piezométrica após a instalação da bomba, nas condições do item anterior. (Sugestão: reveja a equação 1.36, observando os níveis d’água de montante e jusante.) a) hf = J⋅L =150 – 120 = 30 m 2 2 2 5 2 5 2 5 8 9,81 0,3030 30 30 0,117 8 8 0,020 3200 f Q gL Q D Qf Lg D pi pi pi ⋅ ⋅ ⋅ ⋅ = ⇒ = = ⇒ = ⋅ ⋅ ⋅ m3/s b) Pot = ? para Q = 0,15 m3/s ⇒ Q = V⋅A ⇔ 2,1221QV A = = onde 2 0,0707 4 DA pi= = André Barcellos Ferreira – andrepoetta@hotmail.com 6 Universidade Federal do Espírito Santo 9,8 BQ HPot η ⋅ ⋅ = 22 3 2 2 4 1 0,020 3,2 10 4 0,15 1150 120 2 0,3 2 9,80,3a b c B L Q z H z f H D gDpi pi ⋅ ⋅ ⋅ + = + ⇔ + = + ⇔ ⋅⋅ 3 2 2 2 4 0,020 3,2 10 4 0,1530 19,01 0,3 0,3 2 9,8B H pi ⋅ ⋅ ⋅ ⋅ ⇔ = − + = ⋅ ⋅ ⋅ ⋅ 9,8 19,01 0,15 34,93 0,8 Pot ⋅ ⋅∴ = = kW c) 2 2 1 12 2 A A antes A antes A B A B p V p V p z z H z z H g gγ γ γ + + = + + + ∆ ⇔ = + + ∆ 1150 135antes p H γ ∴ = + + ∆ onde: 2 2 1 0,02 533,33 2,1221 8,17 2 2 9,8 0,3 L VH f D g ⋅ ⋅∆ = = = ⋅ ⋅ 6,83antesp γ = mH2O 2 2 1 150 19,01 135 8,172 2 depois depoisA A B B A B p pp V VH z z H g gγ γ γ + + + = + + + ∆ ⇔ = + − − ⇔ 25,84depois p γ ⇔ = mH2O 2.35 Na figura 2.14 os pontos A e B estão conectados a um reservatório mantido em nível constante e os pontos E e F conectados a outro reservatório também mantido em nível constante e mais baixo que o primeiro. Se a vazão no trecho AC é igual a 10 l/s de água, determineas vazões em todas as tubulações e o desnível H entre os reservatórios. A instalação está em um plano horizontal e o coeficiente de rugosidade da fórmula de Hazen- Willians, de todas as tubulações, vale C = 130. Despreze as perdas de carga localizadas e as cargas cinéticas das tubulações. AC BCA B f fCP CP h h= ⇒ = 1,85 ( , ) Hazen Willians J Q tabela D Cβ − = ⋅ → 1,85 1,85 3 1,85 3 1,858100 100 9,686 10 10 100 1,345 10 100AC AC AC BC BC BC BCQ L Q L Qβ β⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⇔ ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⇔ 3 1,85 1,851,85 3 9,686 10 10 509,83 29,07 1,345 10BC Q ⋅ ⋅⇔ = = = ⋅ l/s André Barcellos Ferreira – andrepoetta@hotmail.com 7 Universidade Federal do Espírito Santo 29,07 10 39,07CD BC ACQ Q Q= + = + = l/s DEE F f f DFCP CP h h= ⇒ = ( , ) ( , )DE DF DE DF D C D C β β = = 1,85 1,85 1,85 1,85 1,85250100 100 200 DF DE DE DE DF DF DF DE DF DF DE LQ L Q L Q Q Q L β β⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⇔ = = ⇔ ( )1,851,85 1,851,25 1,128DE DF DE DFQ Q Q Q⇔ = ⇒ = Conservação da matéria ⇒ QDE + QDF = QCD 39,1 1,128 39,1 18,37DE DF DF DF DFQ Q Q Q Q⇔ + = ⇔ + = ⇒ = l/s ⇒ QDE = 20,73 l/s AC CD DEA E f f fH CP CP h h h= − = + + ⇔ 1,85 1,85 1,851 100 AC AC AC CD CD CD DE DE DE H Q L Q L Q Lβ β β = ⋅ ⋅ + ⋅ ⋅ + ⋅ ⋅ ⇔ 3 1,85 2 1,85 3 1,851 9,686 10 0,01 100 3,312 10 0,0391 300 1,345 10 0,02073 200 100 H ⇔ = ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ + ⋅ ⋅ ⋅ ⇔ 6,47H⇔ = m 2.36 Determine o valor da vazão QB, e a carga de pressão no ponto B, sabendo que o reservatório 1 abastece o reservatório 2 e que as perdas de carga unitárias nas duas tubulações são iguais. Material: aço soldado revestido com cimento centrifugado. Despreze as perdas localizadas e as cargas cinéticas. 810 800 0,00758 860 460AB BC J J −= = = + m/m Aço soldado revestido com cimento centrifugado. C = 130 β1 = 1,345⋅103, β2 = 9,686⋅103 1,85 3 1,850,758 1,345 10 0,0175AB AB AB ABJ Q Q Qβ= ⋅ ⇒ = ⋅ ⋅ ⇒ = m3/s = 17,5 l/s 1,85 3 1,850,758 9,686 10 0,00603BC BC BC ABJ Q Q Qβ= ⋅ ⇒ = ⋅ ⋅ ⇒ = m3/s = 6,03 l/s QB = QAB – QBC ⇒ QB = 11,47 l/s Cota B = 810 – ∆HAB = 810 – JABLAB = 810 – 0,00758⋅860 = 803,48 m 803,48 780 23,48Bp γ = − = mH2O 3.1 A instalação mostrada na Figura 3.17 tem diâmetro de 50 mm em ferro fundido com leve oxidação. Os coeficientes de perdas localizadas SAP: entrada e saída da tubulação K = 1,0, cotovelo 90° K = 0,9, curvas de 45º K = 0,2 e registro de ângulo, aberto, K = 5,0. Determine, usando a equação de Darcy-Weisbach: a) a vazão transportada; b) querendo-se reduzir a vazão para 1,96 l/s, pelo fechamento parcial do registro, calcule qual deve ser a perda de carga localizada no registro e seu comprimento equivalente. André Barcellos Ferreira – andrepoetta@hotmail.com 8 Universidade Federal do Espírito Santo 2 2 1 1 2 2 1 2 ,2 2 p V p V z z perdas g gγ γ + + = + + + onde p1 = p2 =patm 1 2 50 45 5fperdas z z h h∴ = − = + ∆ = − = m a) Fórmula de Darcy-Weisbach: 2 2 2 2 5,0 5,0 2 2 2 2 V L V V V LJL K H f K f K g D g g g D + ⋅ = ∆ ⇒ + ⋅ = ⇔ + =∑ ∑ ∑ Ferro fundido com leve oxidação: ε = 0,30 mm (Tabela 2.2) ( ) ( ) 2 2 2,0 13,0 5,0 25,0 5,0 2 1,0 0,9 2 0,2 5,0 5,0 2 2 9,81 0,05 V L Vf K f g D + + + + = ⇔ + ⋅ + + ⋅ + = ⇔∑ ⋅ ( ) ( ) 2 2900 8,3 5,0 5,0 48,87 0,423 , 19,62 V f f V⇔ + = ⇔ = + 0,30ε = mm, D = 50 mm ( ) ( ) 2 2 21 3,71 1 1 12log 2log 3,71 / 2log 3,71 0,05 / 0,0003 2log618,333 D f Df ε ε = ⇔ = = = = ⋅ 21 5,58 = = 0,032 ∴ 5,0 = 1,987V2 ⇔ V = 1,586 m/s ⇒ Q = V⋅A = 1,586⋅pi⋅0,0252 = 3,114⋅10-3 m3/s b) Q = 1,96 l/s ⇒ 2 2 4 4 0,00196 1,0 0,05 QV Dpi pi ⋅ = = = ⋅ m/s 2 2 2 5,0 2 2 2 L V V V Lf K f K D g g g D + = ⇔ +∑ ∑ ε = 0,30 mm, V = 1 m/s → f = 0,0341 ( )2 2,0 13,0 5,0 25,01,0 0,034 2 1,0 0,9 2 0,2 5,0 2 9,81 0,05 K + + + ∴ + + ⋅ + + ⋅ = ⇔ ⋅ 30,6 3,3 98,1 64,2K K⇔ + + = ⇒ = 2 21,064,2 3,27 2 2 9,81reg Vh K g ∆ = = = ⋅ m 2 2 21,03,27 3,27 0,034 3,27 2 2 0,05 2 9,81 eq eq reg eq eq L Lf V Vh JL L f Dg D g ⋅∆ = ⇒ = ⇔ ⋅ = ⇔ ⋅ ⋅ = ⇔ ⋅ 94,35eqL ≅ m André Barcellos Ferreira – andrepoetta@hotmail.com 9 Universidade Federal do Espírito Santo 3.7 A instalação hidráulica predial da figura está em um plano vertical e é toda em aço galvanizado novo com diâmetro de 1”, e alimentada por uma vazão de 2,0 l/s de água. Os cotovelos são de raio curto e os registros de gaveta. Determine qual deve ser o comprimento x para que as vazões que saem pelas extremidades A e B sejam iguais. Tabela 3.6 – Comprimentos equivalentes: cotovelo 90°_raio curto LE = 0,189 + 30,53D registro_gaveta aberta LE = 0,010 + 6,89D Perdas de carga: 2,0 1,5 0,3 3,80ACL = + + = m ( ) ( )2 0,189 30,53 0,010 6,89 0,388 67,95 0,025 2,09 CAEL D D= + + + = + ⋅ = m 0,5 0,3 (0,8 )CBL x x= + + = + m ( ) ( )2 0,189 30,53 0,010 1,89 2,09 CBEL D D= + + + = m Para que QA = QB, devemos ter: ( ) ( )1,5 3,80 2,09 2,09 0,80 A BA T B Tz JL z JL J x J x+ = + ⇔ + ⋅ + = + + + ⇔ ( )3,0 1,50J x x⇔ − = − Hazen-Williams: 1,85 1,85 1,17 2 2 4 4 0,00169,81 2,04 0,025 V QJ V C D Dpi pi ⋅ = ⇒ = = = ⋅ m/s C = 125 (Tabela 2.4) 1,85 1,85 1,17 2,0469,81 0,2518 125 0,025 J J= ⇒ = m/m Logo: 0,2802 0,8406 1,50 1,83x x x+ = + ⇔ = m 3.8 Dois reservatórios, mantidos em níveis constantes, são interligados em linha reta através de uma tubulação de 10 m de comprimento e diâmetro 50 mm, de P. V. C. rígido, como mostra o esquema da Figura 3.23. Admitindo que a única perda de carga localizada seja devido à presença de um registro de gaveta parcialmente fechado, cujo comprimento equivalente é LE = 20,0 m, e usando a fórmula de Hazen-Williams, adotando C = 145, determine: a) a vazão de canalização supondo que o registro esteja colocado no ponto A; b) idem, supondo o registro colocado no ponto B; c) máxima e mínima carga de pressão na linha, em mH2O, nos casos a e b; d) desenhe em escala as linhas piezométrica e de energia. André Barcellos Ferreira – andrepoetta@hotmail.com 10 Universidade Federal do Espírito Santo Equação da continuidade: 2 2 2 2 A A B B A B p V p V z z perdas g gγ γ + + = + + + • pA = pB (os dois reservatórios com NA = 1,0 m) • vA = vB (vazão constante) perdas = zA – zB = 3,0 m ( ) 1,85 1,85 1,85 1,17 1,85 1,173,0 6,31 6,31 10,0 20,0 3145 0,05T V VJL L C D = = ⋅ ⇔ ⋅ + = ⇔ ⋅ ⋅ 1,85 4,397 2,227V V⇔ = ⇒ = m/s 20,052,27 4,37 4 Q VA pi ⋅= = = l/s a) A pressão é mínima no ponto mais alto e máxima no ponto mais baixo: 1,85 1,85 1,85 1,17 1,85 1,17 2,2276,81 6,81 0,1000 145 0,05 VJ C D = = = ⋅ ⋅ m/m 1 2 3 4 4 A B z m z z z z z = = = = • 2 2 2 1 2 2 1 2 1 2( )2 2 2 A A A E E atm mín mín p V p V p V z z JL z z JL g g gγ γ γ + + = + + + ⇒ = − − − ⇔ 22,2271,0 0,1000 20,0 1,25 2 9,81 A A mín mín p p γ γ ⇔ = − − ⋅ ⇔ = − ⋅ m • 2 2 2 1 4 4 1 4 1 4( )2 2 2 A A A T T atm máx mín p V p V p V z z JL z z JL g g gγ γ γ + + = + + + ⇒ = − − − ⇔ 22,2274,0 0,1000 30 0,75 2 9,81 A A mín máx p p γ γ = − − ⋅ ⇔ = ⋅ m b) • 2 2 2 2 1 2 2 1 2 1 2 2,227( ) 1,0 2 2 2 2 9,81 B B B máx máx máx p V p V p V z z z z g g gγ γ γ + + = + + ⇔ = − − = − ⇔ ⋅ 0,75B mín p γ ⇔ = m • 2 2 2 1 3 2 1 3 1 3( )2 2 2 B B B ATM máx máx p V p V p V z z JL z z g g gγ γ γ + + = + + + ⇔ = − − ⇔ 22,2271,0 0,1000 10 2 9,81 B máx p γ ⇔ = − − ⋅ ⋅ = 2,75 m 3.10 Uma tubulação retilínea de 360 m de comprimento e 100 mm de diâmetro é ligada a um reservatório aberto para a atmosfera, com nível constante, mantido 15 m acima da saída da tubulação. A tubulação está fechada na saída por uma válvula, cujo comprimento André Barcellos Ferreira – andrepoetta@hotmail.com 11 Universidade Federal do Espírito Santo equivalente é de 7,5 m de comprimento da tubulação. Se a válvula é aberta instantaneamente, com escoamento livre, determine o tempo necessário para que a velocidade média atinja 98% da velocidade em condições de regime permanente. Assuma o fator de atrito f = 0,020 e adote como coeficiente de perda de carga na entrada K = 0,5. Sugestão: utilize a Equação 1.11 e a metodologia do problema 1.4. Equação 1.11 → 2 2 1 1 2 2 1 2 122 2 p V p V L dV z z H g g g dtγ γ + + = + + + ∆ + Comprimento equivalente na entrada: Equação 3.16 → eL K D f= ⇒ 0,5 0,1 2,5 0,02e K DL f ⋅ ⋅ = = = m Equação 3.15 → 2 2 eL VH f D g ∆ = ⇒ 2 2(7,5 2,5 360)(0,02) 74 0,1 2 2 V VH g g + +∆ = = ⋅ Equação da energia para A e B: 2 2 2 2 2 2 22 2 2 A A A A p V p V L dV V L dV z z H z H g g g dt g g dtγ γ + + = + + + ∆ + ⇔ = + ∆ + ⇔ 2 2 215 74 36,7347 3,8265 36,7347 15 0 2 2 V V dV dVV g g dt dt ⇔ = + + ⇔ + − = Resolvendo-se a equação diferencial, encontramos V(t). A partir de V(t), calculamos t. 3.13 Sabendo-se que as cargas de pressão disponíveis em A e B são iguais e que as diferenças entre as cargas de pressão em A e D é igual a 0,9 mH2O, determine o comprimento equivalente do registro colocado na tubulação de diâmetro único, assentada com uma inclinação de 2° em relação à horizontal, conforme a Figura 3.26. 2 2 0,9 2 2 A D A D A D D A A p V p V p p z z H z z H z H g gγ γ γ γ + + = + + + ∆ ⇔ − = − + ∆ ⇔ = − + ∆ 2 13,96 0,9 13,96 14,46 400 h sen h H H° = ⇔ = ∴ = − + ∆ ⇔ ∆ = 0H JL∆ = onde 6,98 0,0349 14,86 0,0349 425,79 200 J L L= = ∴ = ⇔ = Como LAD = 400, Le = 25,79. 4.1 Um sistema de distribuição de água é feito por uma adutora com um trecho de 1500 m de comprimento e 150 mm de diâmetro, seguido por outro trecho de 900 m de comprimento e 100 mm de diâmetro, ambos com o mesmo fator de atrito f = 0,028. A vazão total que entra no sistema é 0,025 m3/s e toda água é distribuída com uma taxa uniforme por unidade de comprimento q (vazão de distribuição unitária) nos dois trechos, de modo que a vazão na extremidade de jusante seja nula. Determine a perda de carga total na adutora, desprezando as perdas localizadas ao longo da adutora. André Barcellos Ferreira – andrepoetta@hotmail.com 12 Universidade Federal do Espírito Santo F = 0,028 D1 = 0,15 m L1 = 1500 m D2 = 0,1 m L2 = 900 m Qm = 0,025 m3/s 5 1 2 1,042 10Qq L L − = = ⋅ + m3/ms Para o trecho 1: 5 3 3 1 0,025 1,042 10 1500 9,375 10 /j m jQ Q q L Q m s− −= − ⋅ = − ⋅ ⋅ ⇔ = ⋅ 0,025 0,009375 0,0171875 2 2 m j f f Q QQ Q+ += = ⇔ = m3/s Pela equação universal: 2 2 3 15 5 0,0827 0,028 0,01718750,0827 9,008 10 0,15 ff QJ J D − ⋅ ⋅ ⋅ = = ⇒ = ⋅ m/m Assim: 1 1 1 1 13,512H J L H∆ = ⋅ ⇒ ∆ = m Para o trecho 2: 0 3 m j f QQ Q= → = 2 1 0,01443m J fQ Q Q= ⇒ = m3/s 2 2 3 25 5 0,0827 0,028 0,014430,0827 6,3528 10 0,15 fQJ f J D − ⋅ ⋅ = = ⇒ = ⋅ m/m 2 2 2 2 5,717H J L H∆ = ⋅ ⇒ ∆ = m Finalmente: 1 2 19,229T TH H H H∆ = ∆ + ∆ ⇔ ∆ = m 4.4 Quando água é bombeada através de uma tubulação A, com uma vazão de 0,20 m3/s, a queda de pressão é de 60 kN/m2, e através de uma tubulação B, com uma vazão de 0,15 m3/s, a queda de pressão é de 50 kN/m2. Determine a queda de pressão que ocorre quando 0,17 m3/s de água são bombeados através das duas tubulações, se elas são conectadas (a) em série ou (b) em paralelo. Neste último caso, calcule as vazões em cada tubulação. Use a fórmula de Darcy-Weisbach. Tubulação A: QA = 0,20 m3/s ∆P = – 60 kN/m2 2 2 1 1 2 2 1 22 2 V p V p z z H g gγ γ + + = + + + ∆ 3 1 2 3 . 60 10 60 6,1224 . 9,89,8 10A A A V const p p H H H z const γ γ → ⋅ − = ∆ ⇔ = ∆ ⇔ ∆ = = → ⋅ m 2 2 2 5 5 50,0827 0,0827 6,1224 1850,801 A A A A A A A A A A A A f L Q f L Q f L QH D D D ∆ = ⇒ = ⇒ = Tubulação B: QB = 0,15 m3/s ∆P = – 50 nK/m2 André Barcellos Ferreira – andrepoetta@hotmail.com 13 Universidade Federal do Espírito Santo 2 2 1 2 2 2 p V p V z z H g gγ γ + + = + + + ∆ . 50 . 9,8A V const H z const → ∆ = → 2 5 5 500,0287 2741,927 9,8 B B B B B B B f L Q f L D D = ⇒ = a) Em série QA = QB ∆H = ∆HA + ∆HB → ∆P = ∆PA + ∆PB 2 50,0827 A A A A A P f LH Q Dγ ∆ ⋅∆ = = ⋅ ⋅ 20,0827 1850,801 0,27 9,8AP∆ = ⋅ ⋅ ⋅ ∆PA = 43,35 kN/m2 2 50,0827 B B B B B P f LH Q Dγ ∆ ⋅∆ = = ⋅ ⋅ 20,0827 2741,927 0,17 9,8BP∆ = ⋅ ⋅ ⋅ ∆PB = 64,22 kN/m2 ∆P = 43,35 + 64,22 = 107,57 kN/m2 b) Em paralelo QA + QB = 0,17 2 2 2 2 A B 5 5H H 0,0827 0,0827 1850,801 2741,927 A B A A B B A B A B L Lf Q f Q Q Q D D ∆ = ∆ ⇔ ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⇔ = ⇔ 43,021 52,363 1,217A B A BQ Q Q Q⇔ = ⇔ = 2,217 0,17 0,0767B BQ Q∴ = ⇔ = m3/s ⇒ QA = 1,217⋅0,0767 = 0,0933 m3/s 2 50,0827 0,0933 9,8 13,06 A A A A A P f LH P H P P D γ γ ∆ ⋅∆ = ⇒ ∆ = ∆ ⋅ ⇔ ∆ = ⋅ ⋅ ⋅ ⇔ ∆ = kN/m2 4.7 O sistema de distribuição de água mostrado na Figura 4.20 tem todas as tubulações do mesmo material. A vazão que sai do reservatório I é de 20 l/s. Entre os pontos B e C, existe uma distribuição em marcha com vazão por metro linear uniforme e igual a q = 0,01 l/(s.m). Assumindo um fator de atrito constante para todas as tubulações, f = 0,020 e desprezando as perdas localizadas e a carga cinética, determine: a) a carga piezométrica no ponto B; b) a carga de pressão disponível no ponto C, se a cota geométrica desse ponto é de 576,00 m; c) a vazão na tubulação de 4” de diâmetro. André Barcellos Ferreira – andrepoetta@hotmail.com 14 Universidade Federal do Espírito Santo Solução 1: 4” = 0,1 m (Caminho 1) 6” = 0,15 m (Caminho 2) 2 2 2 2 A B A B p V p V z z H g gγ γ + + = + + + ∆ onde AA A pCP z γ = + e BB B pCP z γ = + 590 590A B B BCP CP H CP H CP H∴ = + ∆ ⇔ = + ∆ ⇔ = − ∆ Cálculo de ∆H: 2 2 21 2 1 25 5 5 1 2 0,0827 0,0827 0,0827f L f L f LH Q Q Q D D D ⋅ ⋅ ⋅∆ = ⋅ ⋅ ⇒ ⋅ ⋅ = ⋅ ⋅ ⇔ 2 2 1 2 1 25 5 800 750 0,3514 0,1 0,15 Q Q Q Q⇔ ⋅ = ⋅ ⇔ = Mas 1 2 20AQ Q Q+ = = l/s 2 21,3514 20 14,799Q Q⇒ = ⇔ = l/s = 1,48⋅10–2 m3/s ( )2250,02 790590 0,0827 1,48 10 586,420,15BCP −⋅∴ = − ⋅ ⋅ = m Solução 2: Tubo de 6” = 0,15 m e 4” = 0,10 m 1,85 1,85 6 4 6 4 6 6 4 4 1,85 4,87 1,85 4,8710,65 750 10,65 800(0,15) (0,1) Q QH H J L J L C C ∆ = ∆ ⇔ ⋅ = ⋅ ⇔ ⋅ = ⋅ ⇔ ⋅ ⋅ 1,85 1,85 1,85 1,85 1,85 1,856 4 6 4 6 44,87 4,87 750 800 7.717.858,853 59.304.819,31 7,684 0,15 0,1 Q Q Q Q Q Q⇔ = ⇔ = ⇔ = ⇔ 6 43,011Q Q⇔ = Do enunciado, tem-se que Q4 + Q6 = 0,020. Portanto: Q4 = 4,986⋅10–3 m3/s Q6 = 15,014⋅10–3 m3/s Para as respectivas vazões, tem-se: 6 6 2 6 0,8496 / 4 QV Dpi = = m/s 6 4 2 4 0,6348 / 4 QV Dpi = = m/sNa tubulação de 6” de diâmetro, tem-se: 2 2750 0,84960,02 3,6827 2 0,15 2AB AB L VH f H D g g ∆ = = ⋅ ⋅ ⇒ ∆ = m Equação da energia na superfície I e em B: 2 2 1 1 1 590 3,6827 586,31732 2 B B B AB B B p V p V z z H CP CP g gγ γ + + = + + + ∆ ⇔ = + ⇔ = m b) 586,42 576 10,42B C C CB C p p p p z z H H H γ γ γ γ + = + + ∆ ⇔ = + + ∆ ⇔ = − ∆ 0,02 0,01 0,015 2 2BC m j F F Q QQ Q+ += = → = m3/s, André Barcellos Ferreira – andrepoetta@hotmail.com 15 Universidade Federal do Espírito Santo 2 5 0,02 10000,0827 0,015 4,90 0,15 H ⋅∴∆ = ⋅ ⋅ = m 10 42 4,9 5,52Cp γ ∴ = − − = mH2O c) Da letra a, tem-se: Q1 = 0,3514Q2 = 0,3514⋅1,48⋅10–2 = 5,2⋅10–3 m3/s 4.9 No sistema de abastecimento d’água mostrado na Figura 4.21 faz parte de um sistema de distribuição de água em uma cidade, cuja rede se inicia no ponto B. Quando a carga de pressão disponível no ponto B for de 20 mH2O, determine a vazão no trecho AB e verifique se o reservatório II é abastecido ou abastecedor. Nesta situação, qual a vazão QB que está indo para a rede de distribuição? A partir de qual valor da carga de pressão em B a rede é abastecida somente pelo reservatório I? Material das tubulações: aço rebitado novo. Despreze as perdas localizadas e as cargas cinéticas e utilize a fórmula de Hazen-Williams. Tabela 2.4 → C = 110 8” = 0,20 m 6” = 0,15 m carga de pressão disponível no ponto B = 20 mH2O → 20B p γ = mH2O 740BB B pCP z γ = + = m → Em B a cota piezométrica é CPB = 740 m. Como este valor é maior que a cota piezométrica do N. A. de II, este reservatório é abastecido. Por Hazen-Williams: 1,85 1,85 1,85 1,85 4,87 1,85 4,87 10,65 10,65 4,516 110 0,2 AB AB AB Q QJ J Q C D ⋅ ⋅ = = ⇒ = ⋅ ⋅ 1,85 1,851050 4,516 4741,83AB AB AB AB ABH L J H Q Q∆ = ⋅ → ∆ = ⋅ = Equação da energia na superfície do reservatório I e em B: 2 2 1 1 1 754 720 20 142 2 B B B AB AB AB p V p V z z H H H g gγ γ + + = + + + ∆ ⇔ = + + ∆ ⇒ ∆ = m Assim: 1,851,85 314 4741,83 2.95244663 10 0,04291AB ABQ Q −= ⋅ ⇒ = ⋅ = m3/s = 42,91 l/s Como CPB > NAII, o reservatório II é abastecido, ou seja: AB B BCQ Q Q= + C = 110, D = 6” ⇒ β = 1,831⋅103 (Tabela 2.3) Portanto: 1,85 1,8518,31BC BCJ Q J Qβ= ⋅ → = 1,85 1,85650 18,31 11901,5BC BCH L J H Q Q∆ = ⋅ → ∆ = ⋅ ⋅ = Equação da energia superfície do reservatório II e em B: 2 2 2 2 2 2 720 20 7352 2 B B B B AB B AB BC p V p V p z z H z z H H g gγ γ γ + + = + + + ∆ ⇔ + = + ∆ ⇔ + = + ∆ ⇔ 5BCH⇔ ∆ = m André Barcellos Ferreira – andrepoetta@hotmail.com 16 Universidade Federal do Espírito Santo Assim: 1,85 1,855 11.901,5 14,95BC BCQ Q= ⇒ = l/s Finalmente: 42,91 14,95 27,96B AB BC B BQ Q Q Q Q= − ⇔ = − ⇔ = l/s Para a rede ser abastecida somente por I, a cota piezométrica em B deve ser igual ou maior que NA de II. Portanto: 735 735 15B BB B p pCP z γ γ ≥ ⇔ + ≥ ⇔ ≥ mH2O 5.1 As curvas características de duas bombas, para uma determinada rotação constante, são mostradas na tabela a seguir. Uma dessas duas bombas deverá ser utilizada para bombear água através de uma tubulação de 0,10 m de diâmetro, 21 m de comprimento, fator de atrito f = 0,020 e altura geométrica de 3,2 m. Selecione a bomba mais indicada para o caso. Justifique. Para a bomba selecionada, qual a potência requerida? Despreze as perdas localizadas. Q (m3/s) 0 0,006 0,012 0,018 0,024 0,030 0,036 Bba A H (m) 22,6 21,9 20,3 17,7 14,2 9,7 3,9 ηηηη (%) 0 32 74 86 85 66 28 Bba B H (m) 16,2 13,6 11,9 11,6 10,7 9,0 6,4 ηηηη (%) 0 14 34 60 80 80 60 Para a tubulação, 2 2 5 0,0827 3,2 3473,4g g F QE H H H L E Q D ⋅ ⋅ = + ∆ = + ⇒ = + Para as vazões marcadas, ( ) ( ) 3 / 0,0 0,006 0,012 0,018 0,024 0,03 0,036 3,20 3,32 3,70 4,32 5,20 6,33 7,70 Q m s E m Então, no ponto de funcionamento de A, Q1 = 0,030 m3/s → η1 = 66 % Q2 = 0,036 m3/s → η2 = 28 % QA = 0,033 m3/s Interpolando, 1 1 2 1 2 1 0,033 0,03 66 47 0,036 0,03 28 66 A A A A Q Q Q Q η η η η η η − − − − = ⇒ = ∴ = − − − − % Fazendo o mesmo para o ponto B, tem-se: Q1 = 0,030 m3/s → η1 = 80 % Q2 = 0,036 m3/s → η2 = 60 % QA = 0,035 m3/s Interpolando, tem-se: 1 1 2 1 2 1 0,035 0,03 80 63,33 % 0,036 0,03 60 80 B B B A Q Q Q Q η η η η η η − − − − = ⇒ = ∴ = − − − − ⇒ O melhor rendimento é o da bomba B. Para encontrar a potência requerida, usaremos o ponto (QB, HB) do funcionamento de B. Pela equação de B, tem-se: 2396,83 222,62 15,536BH Q Q= − − + Para Q = 0,035 m3/s, HB = 7,26 m. Com os valores de Q e H, 9800 0,035 7,26 3,93 0,6333 Q HPot γ η ⋅ ⋅ ⋅ ⋅ = = = kW André Barcellos Ferreira – andrepoetta@hotmail.com 17 Universidade Federal do Espírito Santo 5.2 O esquema de bombeamento mostrado na Figura 5.21 é constituído de tubulações de aço com coeficiente de rugosidade da fórmula de Hazen-Williams C = 130. Da bomba até o ponto B, existe uma distribuição de vazão em marcha com taxa de distribuição constante e igual a q = 0,005 l/(SM). Para a curva característica da bomba, dada na figura, determine a vazão que chega ao reservatório superior e a cota piezométrica no ponto B. Despreze as perdas localizadas e a carga cinética. ( ) 2 2 A A C C A C AC C A AC AB AB BC BC 1,85 1,85 1 2 1,85 4,87 4,87 A B A f A 1 B A AB A 2 1,85 A 1,85 P V P V z E z H 2 2 E z z H E 5 J L J L 10,65 Q QE 5 1000 800 130 0,1524 0,1016 Q QQ Q Q 0,0025 Q 2 Q Q qL Q 0,005 Q Q 0,002510,65E 5 130 + + + = + + + ∆ γ γ = − + ∆ ⇒ = + + = + ⋅ + ⋅ + = = = − = = − = − = − = + ( ) ( ) ( ) 1,85 A 4,87 4,87 1,85 1,85 A A Q 0,005 1000 800 0,1524 0,1016 5 12.457,12 Q 0,0025 71.179,3 Q 0,005 − ⋅ + ⋅ = + − + − Q 5 10 15 20 H 20 17,5 12,5 5 E 5,2 10,4 23,1 42,3 Interpolando: ( ) ( ) C B A AB 17,5 x 10,4 x 12,7 17,5 x 5 10,4 x 222,25 12,7x 52 5x 17,5 12,5 10,4 23,1 x 15,7 m/ E H 10 y 17,5 15,7 10,y 1,8 y 11,8 Q 10 15 17,5 12,5 Q Q Q qL 11,8 5 6,8 /s − − = ⇔ − − = − ⇔ − + = − ⇔ − − ⇔ = = = − − = ⇔ = − ⇔ = = − − = = − = − = ℓ ℓ A cota piezométrica em B é: 2 2 A A B B A B AB 1,85 B 1,85 4,87 F B P V P V z E z H 2 2 10,65 0,009315,7 CP 1000 130 0,1524 11,8 6,8Q 9,3 2 CP 15,7 2,2 13,5 m + + + = + + + ∆ γ γ = + ⋅ ⋅ + = = = − = André Barcellos Ferreira – andrepoetta@hotmail.com 18 Universidade Federal do Espírito Santo 5.4 Deseja-se recalcar 10 ℓ/s de água por meio de um sistema de tubulações, com as seguintes características: funcionamento contínuo 24 h, coeficiente de rugosidade da fórmula de Hazen-Williams C = 90, coeficiente da fórmula de Bresse K = 1,5 diâmetro de recalque igual ao diâmetro de sucção, comprimentos reais das tubulações de sucção e recalque, respectivamente, de 6,0 m e 674,0 m, comprimentos equivalentes das peças existentes nas tubulações de tubulação e recalque, respectivamente, de 43,40 m e 35,10 m, altura geométrica de 20 m. Com a curva característica de uma bomba, indicada na Figura 5.22, determine:a) Associando em paralelo duas destas bombas, obtém-se a vazão desejada? b) Em caso afirmativo, qual a vazão em cada bomba? c) Qual a vazão e a altura de elevação fornecidas por uma bomba isoladamente isolada no sistema? d) Que verificações devem ser feitas antes de escolher a bomba, de acordo com os pontos de funcionamento obtidos? ( ) ( ) AB BC 2 2 A A C C A C AC AB T BC T 1,85 1,85 1,85 1,85 4,87 1,85 4,87 P V P V z E z H 2 2 E 20 J L J L 10,65 Q 10,65 QE 20 6 43,40 647 35,1 20 19.438Q 90 0,15 90 0,15 + + + = + + + ∆ γ γ = + + = + + + + = + Tabela para a bomba sozinha: Q 0 2 4 6 7 H 30 28,5 26 22 18,5 E 20 20,2 20,7 21,5 22 Tabela para as bombas em paralelo: Q 0 4 8 12 H 30 28,5 26 22 E 20 20,7 22,6 25,4 Interpolando: ( ) ( ) 1,85 3 26 x 22,6 x 2,8 2,6 x 4 22,6 x 72,8 2,8x 90,4 4x 26 22 22,6 25,4 x 24 m E 24 20 19.438Q Q 0,010 m /s (sim) − − = ⇔ − − = − ⇔ − + = − ⇔ − − ⇔ = = ∴ = + ⇔ = b) 5 ℓ/s André Barcellos Ferreira – andrepoetta@hotmail.com 19 Universidade Federal do Espírito Santo c) ( ) ( ) 1,85 26 x 22 x 21,5 x 0,5 22 x 3,5 21,5 x 11 0,5x 75,25 3,5x 26 22 22 18,5 21,5 22 x 21,6 m H 21,6 20 19.438Q Q 6,2 /s (sim) − − − = ⇔ ⇔ − − = − ⇔ − + = − ⇔ − − − ⇔ = = ∴ = + ⇔ = ℓ 5.6 Considere um sistema de abastecimento de água por gravidade entre dois reservatórios mantidos em níveis constantes e iguais a 812,00 m e 800,00 m, ligados por uma tubulação de 6” de diâmetro, 1025 m de comprimento e fator de atrito f = 0,025. Desejando-se aumentar a capacidade de vazão do sistema, instalou-se, imediatamente na saída do reservatório superior, uma bomba centrífuga cuja curva característica é dada na tabela a seguir. Desprezando as perdas de carga localizadas e a perda de carga na sucção, determine a nova vazão recalcada. Observe que, no caso, a altura geométrica da Equação 5.38 é negativa. Q (m3/s) 0 0,006 0,012 0,018 0,024 0,030 0,036 H (m) 22,6 21,9 20,3 17,7 14,2 9,7 3,9 η (%) 0 32 74 86 85 66 28 2 2 5 QE 12 H 12 JL 12 1025 0,0827f 12 25.777,72Q 0,1524 = − + ∆ = − + = − + ⋅ = − + Com uma equação para E chegamos à tabela: Q (m3/s) 0 0,006 0,012 0,018 0,024 0,030 0,036 H (m) 22,6 21,9 20,3 17,7 14,2 9,7 3,9 E (m) –12 –11 –8,3 –3,6 2,8 11,2 21,4 Interpolando: ( ) ( ) 2 14,2 x 2,8 x 8,4 14,2 x 4,5 2,8 x 119,28 8,4x 12,6 4,5x 14,2 9,7 2,8 11,2 x 10,22 10,22 12 25.777,72Q Q 29,3 / s CP z E 812 10,22 822,22 m − − = ⇔ − − = − ⇔ − + = − ⇔ − − ⇔ = ⇒ = − + → = = + = + = ℓ Q 0,024 0,030 H 14,2 9,7 Η 8 66 Interpolando para o rendimento, vem: 14,2 10,22 85 y 0,88 9 85 y y 77,08 % 14,2 9,7 85 66 − − = ⇔ ⋅ = − ⇔ = − − Portanto: 3 3HQ 9,8 10 10,22 29,3 10Pot 3,8 kW 0,7708 −γ ⋅ ⋅ ⋅ ⋅ = = = η 5.8 Um sistema de bombeamento é constituído por duas bombas iguais instaladas em paralelo e com sucções independentes, com curva característica e curva do N. P. S. H. dadas na Figura 5.23. As tubulações de sucção e recalque tem diâmetro de 4”, fator de atrito f = 0,030 e os seguintes acessórios: na sucção, de 6,0 m de comprimento real, existe uma válvula de pé com crivo e uma curva 90° R/D = 1. O nível d’água no poço de sucção varia com o tempo, atingindo, no verão, uma cota máxima de 709,00 m e, no inverno, uma cota mínima de 706,00 m. A cota de instalação do eixo da bomba vale 710,00 m. verifique o comportamento do sistema no inverno e no verão, determinando os pontos de funcionamento do sistema (Q e H), os valores do N. P. S. H. disponível nas duas estações e o comportamento da bomba quanto à cavitação.. Assuma temperatura d’água, em média, igual a 20°C. André Barcellos Ferreira – andrepoetta@hotmail.com 20 Universidade Federal do Espírito Santo ( ) ( ) ( ) ( ) 1 2 R 1 bomba: Q l/s 0 3 6 9 12 15 18 1 bomba: Q l/s 0 6 12 18 24 30 36 H m 24 22,5 20 17 13 7 0 NPSH m x 2,5 3,5 4,5 5 4,5 9 Válvula de pé com crivo → 1L 0,56 255,48D= + Curva 90° R/D = 1 → 2L 0,115 15,53D= + Válvula de retenção leve → 3L 0,247 79,43D= + Registro de globo → 4L 0,01 340,27D= + r s e 3 4 2 S r e 1 2 L L L 2L 46,563 m L 6 mD 4" 0,1 m L 70 m L L L 27,776 mf 0,030 T 20 C = + + = == = = = + == = ° ( ) ( ) [ ] s rs r s e s r e r 2 2 5 H H H H L L J L L J 0,0827QH 6 27,776 70 45,563 H 37.051Q D ∆ = ∆ + ∆ ⇔ ∆ = + + + ⇔ ⇔ ∆ = + + + ⇔ ∆ = Inverno: 2iE 13 37051Q= + Verão: 2iE 10 37051Q= + Q (l/s) 0 6 12 18 24 30 36 Ev 10 11,33 15,33 22 31,34 43,35 58,02 Ei 10 14,33 18,33 25 34,34 46,35 61,02 Verão: ( ) ( ) ( ) 2 v v v v Q l/s 12 Q 18 E m 15,33 H 22 H m 20 H 17 Inverno: v v v v v v 15,33 H 20 H H 18,55 m 15,33 22 20 17 12 Q 20 H Q 14,9 l/s 12 18 20 17 − − = ⇒ = − − − − ∴ = ⇒ = − − i i i i i i 18,33 H 20 H H 19,48 m 18,33 25 20 17 12 Q 20 H Q 13,04 l/s 12 18 20 17 − − = ⇒ = − − − − ∴ = ⇒ = − − André Barcellos Ferreira – andrepoetta@hotmail.com 21 Universidade Federal do Espírito Santo ( ) ( ) ( ) 2 i v i i Q l/s 12 Q 18 E m 18,33 H 25 H m 20 H 17 Temos que a vd s p pNPSH z H .−= − − ∆ γ Pela tabela da página 158 – T = 20°C – vp 0,24.=γ Portanto: ( ) ( ) ( ) s 2 2 d s e 5 5 Q QNPSH 9,55 0,24 z L L 0,0827f 9,31 z 6 27,776 0,0827 0,03 D 0,1 = − − − + = − − + ⋅ Inverno: i 2 dNPSH 5,31 8379,8Q= − Verão: v 2 dNPSH 8,31 8379,8Q= − v i r 1 d d d Q 0 3 6 9 12 15 18 NPSH 8,31 8,23 8,01 7,63 7,10 6,42 5,59 NPSH 5,31 5,23 5,01 4,63 4,10 3,42 2,59 NPSH x 2,5 3,5 4,5 5 7,5 9 Verão: i r máx d v d v Q 12 Q 15 NPSH 7,1 y 6,42 NPSH 5 y 7,5 Inverno: v r máx d i d i Q 9 Q 12 NPSH 4,63 y 4,10 NPSH 4,5 y 5 ⇒ Há cavitação, já que máxv v Q Q> e máxi iQ Q .> Calculando o NPSHd: 2 i i 2 vv NPSH 5,31 8379,8Q Inverno: NPSH 3,88 m Verão: NPSH 6,45 mNPSH 8,31 8379,8Q = − = ⇒ == − 5.14 Uma bomba centrífuga está montada em uma cota topográfica de 845,00 m, em uma instalação de recalque cuja tubulação de sucção tem 3,5 m de comprimento, 4” de diâmetro, em P. V. C. rígido, C = 150, constando de uma válvula de pé com crivo e um joelho 90°. Para um recalque de água na temperatura de 20°C e uma curva do N. P. S. H. requerido dada pala Figura 5.25, determine a máxima vazão a ser recalcada para a cavitação incipiente. Se a vazão recalcada for igual a 15 l/s, qual a folga do NPSH disponível e do NPSH requerido. Altura estática de sucção igual a 2,0 m e a bomba é não afogada. v v v máx v máx 7,1 y 5 y y 6,65 m 7,1 6,42 5 7,5 12 Q 5 y Q 13,98 l/s 12 15 5 7,5 − − = ⇒ = − − − − ∴ = ⇒ = − − i i i máx i máx 4,63 y 4,5 y y 4,57 m 4,5 4,10 4,5 5 9 Q 4,5 y Q 9,42 l/s 9 12 4,5 5 − − = ⇒ = − − − − ∴ = ⇒ = − − André Barcellos Ferreira – andrepoetta@hotmail.com 22 Universidade Federal do Espírito Santo 1 2 e e D 4” 0,1 m C 1560 L 28,6 m L 4,3 m T 20°C = = = = = = ( ) ( ) 1 2 1,85 e e e 1,85 4,87 1,85 1,85 4,87 1,85 Q 10,65H L L L C D Q 10,65H 3,5 28,6 4,3 150 0,1 H 2708,2 Q ⋅∆ = + + ⋅ ⋅∆ = + + ⋅ ∆ = ⋅ a a 2 p 760 0,081h13,6 1000 h 845 p 9,40 mH O − = γ ↓ = = γ 1,85a v v d v 1,85 d p p pNPSH z H 9,40 2 2708,2Q Tabela da página 158 pT 20 C 0,24 NPSH 7,16 2708,2Q − = − − ∆ = − − − γ γ ↓ = ° → = γ = − Q(l/s) 0 5 10 15 20 25 30 NPSHr (m) 0 0,6 1,2 2,8 5,2 7,6 11,2 NPSHd (m) 7,16 7,01 6,62 6,02 5,21 4,22 3,04 A interseção de NPSHr e NPSHd é em Q = 20 l/s. ⇒ Qmáx = 20 l/s. A folga para Q = 15 l/s é: Folga 6,02 2,8 3,22= − = 6.1 O sistema de recalque mostrado na Figura 6.9 faz parte de um projeto de irrigação que funciona 5 horas e meia por dia. O sistema possui as seguintes características: a) tubulação de sucção com 2,5 m de comprimento, constando de uma válvula de pé com crivo e uma curva 90º R/D = 1; b) uma bomba que mantém uma altura total de elevação de 41,90 m, para a vazão recalcada; c) uma caixa de passagem, em nível constante, com NA = 26,91 m; d) vazão de distribuição em marcha (vazão unitária de distribuição) constante a partir do ponto A igual a q = 0,02 /(sm). Determine: a) os diâmetros de recalque e sucção (adotar o mesmo) usando a Equação 5.18 (ver a Seção 5.4.3); b) a carga de pressão disponível imediatamente antes e depois da bomba; c) os diâmetros dos trechos AB e BC, sendo o ponto C uma ponta seca, vazão nula. Dimensione os diâmetros pelas vazões de montante de cada trecho; d) a potência do motor elétrico comercial. Dados: a) rendimento da bomba: 65%; b) material de todas as tubulações: ferro fundido novo (C=130); c) utilize a equação de Hazen-Williams; d) perdas de carga localizadas no recalque, desprezíveis. André Barcellos Ferreira – andrepoetta@hotmail.com 23 Universidade Federal do Espírito Santo a) A vazão de sucção é: 3(240 108) 9,96 10Q q −= + = ⋅ m3/s Equação 5.18 → 34( ) 1,3 ( / ) ,rD m X Q m s= em que X é a fração do dia de funcionamento do sistema. 5,5 0,229 24 X = = e ( )0,02 240 108 6,96Q = ⋅ + = l = 6,96⋅10–3 m3/s 341,3 0,229 6,96 10 0,0750rD −∴ = ⋅ = m b) Equação da energia em NAI e imediatamente antes de B: 2 2 2 2 1 1 1 0 0 1,22 2 2 2 B B B B B B B m B m m p V p V p V p V z z H z H H g g g gγ γ γ γ + + = + + + ∆ ⇔ = + + + ∆ ⇔ = + + + ∆ 3 2 3 6,96 10 1,57 / 4 4,418 10B Br QV V Dpi − − ⋅ = = ⇒ = ⋅ ⋅ m/s Tabela 3.6 → 1 2 ( ) : 0,56 255,48 19,721 ( ) : 0,115 15,53 1,31975 e e i Crivo L D ii Curva L D = + = = + = ( ) ( )1 2 1,85 1,85 4,8723,541 10,65 0,945m s e e m QH L L L J H C D ∆ = + + ⋅ = ⋅ ⋅ ⇔ ∆ = m ( )21,570 1,2 0,945 2,27 2 9,8 B B antes p p γ γ ∴ = + + + ⇒ = − ⋅ mH2O Equação da energia em NAI e imediatamente depois de B: ( ) 2 2 2 1 1 1 1,571,2 0,945 2 2 2 9,8 B B B B m p V p V pH z z H H II g gγ γ γ + + + = + + + ∆ ⇔ = + + + ⋅ Temos _ 2.3 4 130 3,932 10 0,075 TabelaC D m β= → = ⋅ = ( )1,854 31,85 3,932 10 6,96 10 350 14 100 100j j j j j QH L J L Hβ − ⋅ ⋅ ⋅ ⋅∆ = = = ⋅ ⇔ ∆ = m Como (26,91 0) 0,945 14 41,855j m m jH z z H H= − + ∆ + ∆ = − + + = m, voltando a II, temos: 21,5741,855 1,2 0,945 39,58 2 9,8 B B depois p p γ γ = + + + ⇔ = ⋅ mH2O c) Em A, André Barcellos Ferreira – andrepoetta@hotmail.com 24 Universidade Federal do Espírito Santo QA = 6,96⋅10–3 m3/s Em B, ( ) ( )3 5 36,96 10 2 10 240 2,16 10B A AB BQ Q q L Q− − −= − ⋅ = ⋅ − ⋅ ⋅ ⇒ = ⋅ m3/s Pela Tabela 6.1, tem-se 6,96AQ = l/s < 3,14 l/s ⇒ DAB = 0,125 m. QB = 2,16 l/s < 3,14 l/s ⇒ DBC = 0,075 m d) Equação da energia em B e no NAII, 2 2 2 2 2 22 2 B B B B AB B AB p V p V p z z H z z H g gγ γ γ + + = + + + ∆ ⇔ = + + ∆ ⇔ 26,91 16,71 B AB p H γ ⇔ = + + ∆ (III) Temos _ 2.3 3 130 3,267 10 0,125 TabelaC D m β= → = ⋅ = ( )1,853 31,85 240 3,267 10 2,16 10 0,092 100 100 B AB AB AB AB AB QH L J L Hβ − ⋅ ⋅ ⋅ ⋅ ⋅∆ = ⋅ = ⋅ = ⇒ ∆ = Voltando a III, temos: 26,91 16,71 0,092 10,12B Bp p γ γ = + + ⇔ = mH2O e) 39,8 41,855 6,96 10 4,39 0,65 H QPot Potγ η − ⋅ ⋅ ⋅ ⋅ ⋅ = = ⇒ = kW 3 3 310 10 6,96 10 41,855 5,97 75 75 0,65 H QPot Pot η − ⋅ ⋅ ⋅ ⋅ ⋅ = = ⇒ = ⋅ cv 6.2 A rede de distribuição de água, representada na Figura 6.10, possui as seguintes características: a) os trechos BC, CE, EF, CD e EG têm uma vazão de distribuição em marcha constante e igual a q= 0,010 l/(sm) b) os pontos D, F e G são pontas secas; c) as cotas topográficas dos pontos são: ( ) 6,0 7,0 8,0 11,0 8,0 10,0 6,0 Ponto A B C D E F G Cota m Determine a cota do nível de água no reservatório, para que a mínima carga de pressão dinâmica na rede seja de 12 mH2O. Determine a máxima carga de pressão estática. Material das tubulações tem C = 130. André Barcellos Ferreira – andrepoetta@hotmail.com 25 Universidade Federal do Espírito Santo EXEMPLO 8.1 Estime o valor do fator de atrito f, do coeficiente de rugosidade C de Chézy e do coeficiente de rugosidade n de Manning em um canal largo de 1,50 m de profundidade, no qual as medidas de velocidades a 20 % e 80 % da altura d’água foram, respectivamente, v0,20 = 0,80 m/s e v0,80 = 1,20 m/s. Assuma distribuição de velocidade logarítmica na vertical, escoamento turbulento rugoso e que a altura d’água é igual ao raio hidráulico. A Equação 2.31 * 8,48 2,5lnv R u ε = + , desenvolvida a partir da hipótese de perfil logarítmico, pode ser posta em forma mais conveniente como: * 29,845,75logv R u ε = Em que y é uma ordenada medida a partir do fundo e v, a velocidade pontual. Para y = 0,80h e y = 0,20h, fica: 0,80 * 23,875,75log v h u ε = 0,20 * 5,975,75log v h u ε = Fazendo 0,80 0,20 v X v = , dividindo uma equação pela outra e desenvolvendo, vem: 0,776 1,378log 1 h X Xε − = − Usando o conceito de diâmetro hidráulico, a velocidade média é dada pela equação 2.32 * 2,5ln 4,73V R u ε = + , na forma: * 25,75log 4,73 5,75log 4,73 5,75log 4,73 5,75log 6,46 2 hV R D R h u ε ε ε ε = + = + = + = + Pela equação 2.26 * 8V u f = , que relaciona a velocidade média com o fator de atrito, tem-se: * 8 0,776 1,378 2 1,4646,46 1 1 V X X u f X X − + = = + = − − Para 1,20 1,5, 0,80 X = = o fator de atrito vale f = 0,100 e da Equação 8.7 0 0 8 8 ,h h g gV R I V C R I Cf f = ⇔ = ⇐ = 8 78,4 28 0,100 gC f= = = e, finalmente, como h = Rh = 1,50 m e 1/6 hRC n = o coeficiente de rugosidade de Manning vale n = 0,038. EXEMPLO 8.2 Determinar a altura d’água em uma galeria de águas pluviais, de concreto n = 0,013, diâmetro igual a 0,80 m, declividade de fundo I0 = 0,004 m/m, transportando uma vazão de 600 l/s em regime permanente e uniforme. O coeficiente dinâmico vale: André Barcellos Ferreira – andrepoetta@hotmail.com 26 Universidade Federal do Espírito Santo 3/8 3/8 0 0,013 0,60 0,456 0,004 nQM I ⋅ = = = Pela Equação 8.47 1 MD K = : 1 1 0,4560,80 0,570K K = ∴ = Na Tabela 8.1, para K1 = 0,570, determina-se o valor da lâmina d’água relativa, isto é, a altura normal dividida pelo diâmetro. Para K1 0,570, tira-se y0/D = 0,625, e daí y0 = 0,50 m. EXEMPLO 8.3 Qual a relação entre as vazões transportadas, em regime permanente e uniforme, em uma galeria de águas pluviais, com lâmina d’água igual a 2/3 do diâmetro e a meia seção. Na Tabela 8.1, para lâminas d’água iguais a y0/D = 0,666 e y0/D = 0,50 m, os coeficientes K1 valem, respectivamente, 0,588 e 0,498. Pela Equação 8.47 3/8 1 0 , em que M= ,M nQD K I = fórmula de Manning, como o diâmetro é o mesmo, tem-se: 1 2 1 1 2 2 1,18MM M K K M = ∴ = e para a mesma declividade e rugosidade, fica: 3/8 1 1 2 2 1,18 1,56Q QQ Q = ∴ = EXEMPLO 8.4 Dimensione um canal trapezoidal dom taludes 2H:1V, declividade de fundo I0 = 0,0010 m/m, revestimento dos taludes e fundo em alvenaria de pedra argamassada em condições regulares, para transportar uma vazão Q = 6,5 m3/s. Utilize uma razão de aspecto m = b/y0 = 4. Calcule a velocidade média e verifique se a seção encontrada é de mínimo perímetro molhado. Na Tabela 8.5, determina-se o coeficiente de rugosidade n = 0,025. Na Tabela 8.2, determina-se o coeficiente de forma K, em função de m = 4 e Z = 2, e vale K = 1,796. O coeficiente dinâmico vale: 3/8 3/8 0 0,025 6,5 1,847 0,001 nQM I ⋅ = = = Pela fórmula de Manning, Equação 8.39 3/8 0 0 , em que :M nQy M K I = = 0 1,847 1,03 1,796 My K = = = m Então: 0 4 4,12bm b y = = ∴ = m (largura do fundo) A área molhada vale: ( ) ( )2 20 4 2 1,03 6,36A m Z y= + = + ⋅ = m2. André Barcellos Ferreira – andrepoetta@hotmail.com 27 Universidade Federal do Espírito Santo A velocidade média é igual a 6,5 1,02 6,36 QV A = = = m/s. Para que a seção dimensionada tenha o mínimo perímetro molhado, é necessário que seja verificada a Equação 8.53, isto é: ( ) ( )22 1 2 1 4 2 0,47 4m Z Z= + − = + − = ≠ Conclusão: a seção não é de mínimo perímetro molhado. 8.1 Um canal de drenagem, em terra com vegetação rasteira nos taludes e fundo, com taludes 2,5H:1V, declividade de fundo I0 = 30 cm/km foi dimensionado para uma determinada vazão de projeto Q0, tendo-se chegado a uma seção com largura de fundo b = 1,75 m e altura de água y0 = 1,40 m. a) Qual a vazão de projeto? b) A vazão encontrada é de mínimo perímetro molhado? c) Se o projeto deve ser refeito para uma vazão Q1 = 6,0 m3/s e a seção é retangular, em concreto, qual será a altura de água para uma largura de fundo igual ao dobro da anterior? Taludes 2,5H:1V → Z = 2,5 Q0: vazão de projeto I0 = 30 cm/km = 0,0003 m/m B= 1,75 m y0 = 1,4 m a) Q0 = ? 3/8 0 , nQM I = onde 0 1,4 1,423 1,9922M y K M= ⋅ ⇔ = ⋅ = 3/8 43/8 3/8 4 4 0,025 0,025 1,9922 3 101,78 1,9922 4,35 0,0253 10 3 10 Q Q Q − − − ⋅ ⋅ ⇒ = ⇒ = ⇒ = = ⋅ ⋅ m3/s b) ( ) ( )2 22 1 2 1 2,5 2,5 0,3852 1,25m Z Z= + − = + − = ≠ ∴ não c) 3 1 6,0 m / 0,014 ' 2 3,5 Q s seção circular concreto n b b = ⇒ = = = 8/3 8/3 40 0,014 6 0,1717 3,5 3 10 n QK K b I − ⋅ ⋅ = ⇒ = = ⋅ Pelo ábaco, 0 00,29 0,29 3,5 1,01 y y b = ⇒ = ⋅ = m 8.2 Uma galeria de águas pluviais de 1,0 m de diâmetro, coeficiente de rugosidade de Manning n = 0,013 e declividade de fundo I0 = 2,5⋅⋅⋅⋅10–3 m/m transporta, em condições de regime permanente uniforme, uma vazão de 1,20 m3/s. a) Determine a altura d’água e a velocidade média. b) A tensão de cisalhamento média, no fundo, e a velocidade de atrito. c) Qual seria a capacidade de vazão da galeria, se ela funciona na condição de máxima vazão? D = 1,0 m N = 0,013 I0 = 2,5⋅10–3 m/m Q = 1,2 m3/s 0 1,75 1,25 1,4 b m y = = = 0 ?y = André Barcellos Ferreira – andrepoetta@hotmail.com 28 Universidade Federal do Espírito Santo a) y0 = ? e V0 = ? 3/83/8 30 0,013 1,2 0,646 2,5 10 nQM I − ⋅ ⇒ = = = ⋅ 0,646 0,646 1 MK D = = = 0 00,85 0,82 y m y D = = → = m Pela Equação 8.58 2/3 2/3 1/2 0 1 1 , 2,52 senV D I n θ θ = − ⋅ com 1 0 22cos 1 ,y D θ − = − tem- se: 1 102 2 0,822cos 1 2cos 1 259,58 1 y D θ − − ⋅ = − = − = ° = 4,53 rad ( ) 2/31/22/3 31 4,531 2,5 10 1 1,53 1,14 1,742,52 0,013 4,53senV V− = ⋅ − → = ⋅ = ⋅ m/s b) 0 ,hR Iτ γ= onde 30 1 0,304 9810 0,304 2,5 10 7,46 4h senD R θ θ τ − − = = ⇒ = ⋅ ⋅ ⋅ = Pa * 0,086hu gR I= = m/s c) Pela Equação 8.59 ( ) 5/3 8/3 1/2 0 2/3 1 20,2 senQ D I n θ θ θ − = , tem-se: ( )5/33 2/3 5,28 5,281 2,5 10 1,29 20,2 5,28 senQ n − − = ⋅ = m3/s 8.4 Um canal trapezoidal deve transportar, em regime uniforme, uma vazão de 3,25 m3/s, com uma declividade de fundo I0 = 0,0005 m/m trabalhando na seção de mínimo perímetro molhado. A inclinação dos taludes é de 0,5H:1V e o revestimento será em alvenaria de pedra argamassada em condições regulares. Determine a altura d’água, a largura de fundo e a tensão média de cisalhamento no fundo do canal. Trapézio: Q = 3,25 m3/s mínimo perímetro y0 = ? n = 0,025 I0 = 0,0005 m/m molhado b0 = ? z = 0,5 (MPM) τ = ? 3/83/8 0,025 3,25 1,62 0,0005 nQM I ⋅ = = = ( )20 0 1,622 1 1,51,1 1,24 1,1 M My MPM m Z Z y t t m t = → = + − = = = = = m 20 , onde R 21,24 1,9 m 1,51,5 9810 0,0005 3,7 N/m 2 h h yR Ib b m b y τ γ τ = ⋅ ⋅ = = ⇒ = ⇔ = = ⋅ ⋅ = André Barcellos Ferreira – andrepoetta@hotmail.com 29 Universidade Federal do Espírito Santo 8.5 Dimensione um canal para irrigação, em terra, com vegetação rasteira no fundo e nos taludes, para transportar uma vazão de 0,75 m3/s, com declividade de fundo I0 = 0,0005 m/m, de modo que a velocidade média seja no máximo igual a 0,45 m/s. Inclinação dos taludes 3H:1V. n = 0,025 Q = 0,75 m3/s I0 = 0,0005 m/m 0,45 m/s 3V z≤ = QV A = 0 My K = 0 0,94nQM I = = ( )0 02A b y y= + ( )22 1 3 3 0,32 1,780m K= + − = ⇒ = 0,750,45 0,45Q A A ≤ ⇔ ≤ 0 0,94 0,53 1,78 y = = m ( ) ( )0 01 12 2 3 0,53 0,53 0,53 0,84272 2A b b Zy y b b b= + + = + + ⋅ ⋅ = + Mas 1,67A ≥ m2 ∴ 0,53 0,8427 1,67 1,56b b+ ≥ ⇔ ≥ m 8.6 Dimensione um canal trapezoidal, com taludes 2H:1V, declividade de fundo I0 = 0,001 m/m, com taludes e fundo em alvenaria de pedra argamassada, em boas condições, para transportar em regime uniforme uma vazão de 8,0 m3/s, sujeita às seguintes condições: a) A máxima altura d’água deve ser de 1,15 m. b) A máxima velocidade média deve ser de 1,30 m/s. c) A máxima largura na superfície livre deve ser de 8,0 m. Canal trapezoidal (alvenaria em pedra argamassada, em boas condições): n = 0,030 Q = 8,0 m3/s I0 = 0,001 m/m y0 < 1,15 m vmáx < 1,30 m/s n < 8,0 m 0 1,15 1,15 1,6 My K K < ⇒ > ⇔ ≥ → da Tabela 8.2, 0 2,8bm y = = 8 8 1,3 6,15máxQ V A v A A A= ⋅ ⇒ = ⋅ ⇔ = ⇔ = m2 Mas ( ) 2 20 0 06,15 (2,8 2) 1,13A m Z y y y= + → = + ⇒ = m 0 0 2,8 2,8 2,8 1,13 3,164bm b y y = = ⇒ = = ⋅ = m 02 3,164 2 2 1,13 7,684B b Z y B= + ⋅ ⋅ → = + ⋅ ⋅ = m 8.8 Um trecho de um sistema de drenagem de esgotos sanitários é constituído por duas canalizações em série, com as seguintes características: Trecho 1 – Diâmetro: D1 = 150 mm Declividade: I1 = 0,060 m/m Trecho 2 – Diâmetro: D2 = 200 mm Declividade: I2 = 0,007 m/m Determine a máxima e a mínima vazões no trecho para que se verifiquem as seguintes condições de norma: a) Máxima lâmina d’água: y = 0,75D b) Mínima lâmina d’água: y = 0,20D c) Máxima velocidade: V = 4,0 m/s 3/83/8 0,020 8 1,84 0,001 nQM I ⋅ = = = André Barcellos Ferreira – andrepoetta@hotmail.com 30 Universidade Federal do Espírito Santo d) Mínima velocidade: V = 0,50 m/s Coeficiente derugosidade de Mannin, n = 0,013. Canalizações em série n = 0,013 ( ) 1 0 2 22cos 1 8 y D D sen A θ θ θ − = − − = 1 1 1: D 150 mm = 0,15 m I 0,060 m/m Trecho = = 2 2 2: 200 mm = 0,2 m I 0,007 m/m Trecho D = = 00,20 0,75D y D≤ ≤ Qmáx = ? e Qmín = ? No caso de y0 = 0,20D, temos: 0 0 10,20 0,20 0,259 yy D K D = ⇔ = → = ( )12cos 1 2 0,2 106,26 1,855 radθ −= − ⋅ = ° = Em 1: 0,15 0,03885 0,259 M M= ⇒ = 3/8 3/8 1 1 0,013 0,03885 0,060,03885 0,0033 0,0130,06 Q Q ⋅= ⇒ = = m3/s Em 2: 3/8 3/8 32 2 0,2 0,0518 0,259 0,013 0,0518 0,0070,0518 0,0024 m /s 0,0130,007 M M Q Q = ⇔ = ⋅ = ⇔ = = Qmín em 1 ⇒ 0,0033 m3/s. Como a tubulação está em série, Qmín = 0,0033 m3/s. Verificando se a vazão mínima atende ao intervalo de velocidade (0,5 m3/s ≤ V ≤ 4 m3/s), temos: 2 0,0033 0,36 0,00911mín mín Q QV A = = = m 3/s No caso y0 = 0,75D, temos: 0 0 10,75 0,75 0,624 yy D K D = ⇔ = → = ( )12cos 1 2 0,75 240 4,189 radθ −= − ⋅ = ° = Em 1: 3/8 1 0 Q V A M nQD M K I = ⋅ = = ( )2 3 3 2 0,2 1,855 1,855 9,11 10 m /s 8 0,0024 0,26 m/s (ok!) 0,00911 sen A v − − = = ⋅ ∴ = = ( )2 3 3 1 0,15 1,855 1,855 2,52 10 m /s 8 0,0033 1,31 m/s (ok!) 0,00252 sen A v − − = = ⋅ ∴ = = André Barcellos Ferreira – andrepoetta@hotmail.com 31 Universidade Federal do Espírito Santo 0,15 0,0936 0,624 M M= ⇒ = 3/8 3/8 31 1 0,013 0,0936 0,060,0936 0,0083 m /s 0,0130,06 Q Q ⋅= ⇒ = = ( )2 2 1 1 4,189 4,189 0,00830,15 0,01422 m 0,58 m/s (ok!) 8 0,01422 sen A V − = = ⇒ = = Em 2: 0,2 0,1248 0,624 M M= ⇒ = 3/8 3/8 32 2 0,013 0,1248 0,0070,1248 0,0250 m /s 0,0130,007 Q Q ⋅= ⇒ = = ( )2 2 2 1 4,189 4,189 0,0250,2 0,0253 m 0,99 m/s (ok!) 8 0,0253 sen A V − = = ⇒ = = ( ) 1 1 0 0 0 0,025 1,76 m/s (ok!) 0,01422 1 cos 2y 0,094 m 2 0,035y 0,1125 (ok!) máxQV A D y θ = = = − = = ≤ ≤ 8.10 Determine a mínima declividade necessária para que um canal trapezoidal, taludes 4H:1V, transporte 6 m3/s de água, com uma velocidade média igual a 0,60 m/s. Coeficiente de rugosidade, n = 0,025. Z = 4 Q = 6 m3/s V = 0,60 m/s n = 0,025 0 ?mínI = Para que I0 seja mínimo, a seção deve ser de mínimo perímetro molhado. Portanto: ( ) ( )2 22 1 2 1 4 4 0,246m Z Z= + − = + − = 0 0 0,246bm b y y = ⇒ = Voltando a A, tem-se: 2 0 04,246 10 1,53 my y= ⇔ = Da Tabela 8.2, interpolando, para m = 0,246, vem K = 1,4465. Assim: 0 1,53 1,4465 2,213145 My M K = ⇒ = ⋅ = 3/8 2 4 0 3/8 0 0,025 6 0,025 62,213145 3,25 10 m/m 2,213145 I I − ⋅ ⋅ = ⇔ = = ⋅ 8.19 Um trecho de coletor de esgotos de uma cidade cuja rede está sendo remanejada tem 100 m de comprimento e um desnível de 0,80 m. Verifique se o diâmetro atual, de 200 mm, permite o escoamento de uma vazão de 18,6 ℓ/s. Em caso contrário, qual deve ser o novo diâmetro desse trecho? Determine a lâmina líquida correspondente e a velocidade média. 30,025 m /smáxQ = 26 10 m 0,6 QQ V A A V = ⋅ ⇒ = = = ( ) ( ) ( ) ( )0 0 0 0 0 0 02 4 102 2 b B y b Z y y A b Zy y b y y + + ⋅ ⋅ = = = + = + = André Barcellos Ferreira – andrepoetta@hotmail.com 32 Universidade Federal do Espírito Santo Material das tubulações: manilha cerâmica, n = 0,013. Adote como lâmina d’água máxima no coletor y0/D = 0,50. Atualmente, D = 200 mm Q = 18,6⋅10–3 m3/s n = 0,013 A máxima lâmina de água: y0 = 0,5D ∴ y0 = 0,1 m Sendo 0y 0,5, D = da Tabela 8.1, temos K1 = 0,498 Sabemos que ( ) 3/8 3/8 8/3 1 1 1 0 0 0 M nQ nQ nQD , onde M DK DK K I I I = = ⇒ = ⇔ = Atribuindo valores: ( )8/3 30,008Q 0,2 0,498 0,01466 m /s 14,67 l/s 0,013 = × = = Portanto, D = 200 mm não é suficiente para Q = 18,6 l/s. Então: 3/8 3/83 30 nQ 0,013 18,6 10M 0,1088 I 8 10 − − ⋅ ⋅ = = = ⋅ Como a relação y0/D não se altera, K1 = 0,498. Logo: 1 MD 0,2186 m K = = Como não existe esse diâmetro comercializado, D = 250 mm 0 0 y 0,5 y 0,108 m D = → = Na seção circular: ( )1 1 102y 2 0,1082cos 1 2cos 1 2cos 0,01189 3,18 rad D 0,2186 − − − ⋅ θ = − = − = = ( ) ( ) ( ) 2 2 3 20,2186 3,18 3,18 5,97 10 3,22 0,0192 m 8 8 − − − = = = ⋅ = D sen sen A θ θ Portanto: 3Q 18,6 10V 0,97 m/s A 0,0192 − ⋅ = = = 8.20 No projeto de um coletor de esgotos, verificou-se que, para atender à condição de esgotamento dos lotes adjacentes, ele deveria ter uma declividade de 0,015 m/m. Sendo 20 l/s a vazão de esgotos no fim do plano e 10 l/s a vazão atual (início de plano), determine: a) o diâmetro do coletor e a velocidade de escoamento, para o final do plano; b) a lâmina líquida atual e a correspondente velocidade média. 3 0I 0,8 m/100 m 8 10 m/m − = = ⋅ André Barcellos Ferreira – andrepoetta@hotmail.com 33 Universidade Federal do Espírito Santo 3 3 j 3 3 m Q 20 l/s 20 10 m /s Q 10 l/s 10 10 m /s − − = = ⋅ = = ⋅ ( )1 102y2cos 1 2cos 0 rad D − − θ = − = = pi a) D = ? e Vj = ? 1 MD K = 3/8 3/83 2 0 nQ 0,013 20 10M 9,5 10 I 0,015 − − ⋅ ⋅ = = = ⋅ 29,95 10D 0,2 m 200 mm 0,498 − ⋅ ⇒ = = = ( ) ( )2 2 20,2 0,0154 m 8 8 − − = = = D sen sen A θ θ pi pi Com a área, temos a velocidade pela relação jj Q V : A = 3j j Q 20 10V 1,29 m/s A 0,0154 − ⋅ = = = b) 3mQ 0,01 m /s= 3/8 3/83 0 nQ 0,013 10 10M 0,077 I 0,015 − ⋅ ⋅ = = = 1 M 0,077D 0,155 m K 0,498 = = = ( ) ( )1 0 0 D 1 cos /2 0,155 1 cos /22y2cos 1 y 0,0775 m D 2 2 − − θ − pi θ = − → = = = ( ) ( )2 2 3 20,155 9,43 10 m 8 8 − − − = = = ⋅ D sen sen A θ θ pi pi 3 m m 3 Q 10 10V 1,06 m/s A 9,43 10 − − ⋅ = = = ⋅ 9.5 Em um projeto de um sistema de drenagem de águas pluviais, determinou-se que, para escoar uma vazão de 12 m3/s, era necessária uma galeria retangular em concreto, rugosidade n = 0,018, declividade de fundo I0 = 0,0022 m/m, com 3,0 m de largura, conforme a figura. Por imposição do cálculo estrutural, foi necessário dividir a seção em duas células de 1,5 m de largura com um septo no meio. Verifique se esta nova concepção estrutural tem condições hidráulicas de escoar a vazão de projeto, em condições de escoamento livre. 0I 0,015m/m= 0 1 n 0,013 y 0,5 D K 0,498 = = = Seção original Seção modificada André Barcellos Ferreira – andrepoetta@hotmail.com 34 Universidade Federal do Espírito Santo ( ) T 1 2 2 h 2 ) Seção modificada Q Q Q n 0,018 b 1,5 m 0,714 y 2,1 Área 1,5 2,1 3,15 m P 1,5 2,1 2 6,3 A 3,15R 0,5 m P 6,3 ° = + = = = = = ⋅ = = + = = == Manning: 2/3 2/3 31 h 1 0 nQ 0,018 QA R 3,15 0,5 Q 5,17m /s I 0,0022 ⋅ = ⋅ ⇒ = ⋅ ⇔ = T 1 2 1 3 T Q Q Q 2Q Q 2 5,17 10,34m /s = + = = ⋅ = Não tem condições.⇒ 9.6 Uma galeria de águas pluviais de seção retangular escoa uma certa vazão, em escoamento uniforme, com uma largura de fundo igual a 0,90 m e altura d’água de 0,70 m. Em uma determinada seção, deverá haver uma mudança na geometria, passando para uma seção circular. Determine o diâmetro da seção circular para transportar a mesma vazão, com a mesma altura d’água, rugosidade e declividade de fundo. 0 0 r c Retangular Circular b 0,9 m D ? y 0,7 m y 0,7 m I I = ⇒ = = = = 1°) 0 0,9 1,29 0,874 0,7 = ⇒ = = → = b m m K y 0 0 3/8 0,7 0,874 0,61 0,61 = ⇒ = ⋅ = ⋅ = = = My M y K K nQM I 2°) 2DA 4 pi ⋅ = P D= pi 2 h A D DR P 4 D 4 pi ⋅ = = = pi 3°) ( ) 2/32 2/38/32/3 2 h 2,67 nQ D D DA R 0,61 0,27 0,79D 4 4 2,52I D 0,86 D 0,95 m pi ⋅ = ⋅ ⇔ = ⋅ ⇔ = ⋅ ⇔ ⇔ = ⇔ = 3 0 1 ) Seção original Q 1 /s2 m n 0,018 I 0,0022 m/m b 3m y 2,1 m ° = = = = = 0 3 1,43 2,1 = ⇒ = = b m m y André Barcellos Ferreira – andrepoetta@hotmail.com 35 Universidade Federal do Espírito Santo 9.8 Qual deve ser a declividade de fundo de um canal trapezoidal com taludes 2H:1V, largura da base b = 3,0 m, para transportar uma vazão de 3,0 m3/s com velocidade média de 0,60 m/s. Coeficiente de rugosidade do fundo e taludes n = 0,018. 3 trapézio z 2 b 3 m Q 3,0 m /s V 0,6 m/s n 0,018 → = = = = = ( ) ( ) ( ) 2 2 2 2 2 2 3Q V A A 5 m 0,6 A m Z y e A 2 1 Z Z y 5 2 1 2 2 y y 1,42 = ⋅ → = = = + = + − ∴ = + − ⇔ = As principais partes constituintes de um vertedor são: a) Crista ou soleira é a parte superior da parede em que há contato com a lâmina vertente. Se o contato da lâmina se limitar, como nos orifícios de parede fina, a uma aresta biselada, o vertedor é de parede delgada; já se o contato ocorrer em um comprimento apreciável da parede, o vertedor é de parede espessa. b) Carga sobre a soleira h é a diferença de cota entre o nível d’água a montante, em uma região fora da curvatura da lâmina em que a distribuição de pressão é hidrostática, e o nível da soleira. Em geral, a uma distância a montante do vertedor igual a seis vezes a carga, a depressão da lâmina é desprezível. c) Altura do vertedor P é a diferença de cotas entre a soleira e o fundo do canal de chegada. d) Largura ou luz da soleira L é a dimensão da soleira através da qual há o escoamento. 12.7 Um vertedor retangular de parede fina com 1,0 m de largura, sem contrações laterais, é colocado juntamente com um vertedor triangular de 90º em uma mesma seção, de modo que o vértice do vertedor triangular esteja 0,15 m abaixo da soleira do vertedor retangular. Determinar: a) a carga no vertedor triangular quando as vazões em ambos os vertedores forem iguais; b) a carga no vertedor triangular quando a diferença de vazão entre o vertedor retangular e triangular for máxima. Utilizar a fórmula de Thomson e Francis. Fórmula de Francis → Q = 1,838bh3/2, onde Q → vazão em m³/s. b → largura do vertedor em metros. h → altura da lâmina d’água sobre a crista do vertedor em metros. Fórmula de Thomson → Q = 1,40h5/2 a) 1 2 1 vertedor retangular , onde 2 triangular Q Q vertedor → = → Usando a fórmula de Thomson para o vertedor triangular e a fórmula de Francis para o vertedor retangular, tem-se: 3/8 = nQM I 0 = My K 3/83/8 0 5 0 b 3 m 2,11 K 1,5 y 1,42 M y K 1,42 1,5 2,13 nQ 0,018 3M 2,13 I I I 5,17 10 m/m− = = = ⇒ ≈ = ⋅ = ⋅ = ⋅ = ⇒ = ∴ = ⋅ André Barcellos Ferreira – andrepoetta@hotmail.com 36 Universidade Federal do Espírito Santo 2 5 3/2 5/2 1 2 3 5 3 2 3 1,8381,838 1,40 1,4 0,58 0,45 0,0675 3,375 10 0 HQ Q L h H h H H H H − = ⇒ ⋅ ⋅ = ⋅ ⇔ = ⇔ ⇔ − + − + ⋅ = Observamos que a soma dos coeficientes é aproximadamente 1, o que nos leva a concluir que existe uma raiz próxima a este valor. Por tentativa e erro: H = 1,04 m b) ( )1 2Q Q− é máxima ( ) ( ) ( )3/23/2 5/2 5/21 2 1,838 1,40 1,838 0,15 1,40 0máx máx dQ Q L h H H HdH − = ⋅ ⋅ − ⋅ → − − = ⇔ ( ) ( )1/2 3/2 2 3 2 32,757 0,15 3,5 7,6 0,15 3,5 3,5 7,6 1,14 0H H H H H H⇔ − = ⇔ − = ⇔ − + = ⇔ H = 0,7 m 12.9 Um vertedor retangular de parede fina, sem contrações laterais, é colocado em um canal retangular de 0,50 m de largura. No tempo t = 0, a carga H sobre a soleira é zero e, com o passar do tempo, varia conforme a equação H = 20⋅⋅⋅⋅t, com H (m) e t (min). Determinar o volume de água que passou pelo vertedor após 2 minutos. VERTEDOR RETANGULAR DE PAREDE FINA SEM CONTRAÇÕES_ equação de Bernoulli: ( ) 2 2 2 0 1 0 1 22 2 2 V V Vh h y V g y g g g + = − + ∴ = + 0,5A h= ⋅ Volume vazão tempo velocidade área tempo= ⋅ = ⋅ ⋅ 12.14 Se a equação básica para um vertedor retangular, de soleira fina, sem contrações laterais, Equação 12.70, for usada para determinar a vazão por um vertedor de soleira espessa, de igual largura, qual deve ser o coeficiente de vazão Cd naquela equação? Despreze a carga cinética de aproximação. Vertedor retangular de parede fina sem contrações → 3/22 2 3 d Q C g L h= ⋅ ⋅ ⋅ (Equação 12.70) Vertedor de soleira espessa horizontal → 3/21,704dQ C b h= ⋅ ⋅ ⋅ (Equação 12.94) Igualando as duas equações, tem-se: 3/2 ' 3/22 22 1,704 2 1,704, 3 3d d d C g L h C b h C g⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⇔ ⋅ = admitindo ' 1dC = 2 12 1,704 0,577 3 3d d C g C⋅ = ⇒ = = 12.18 A captação de água para o abastecimento de uma cidade na qual o consumo é de 250 l/s (vazão de demanda) é feita num curso d’água onde a vazão mínima verificada (no período de estiagem) é de 700 l/s e a vazão máxima verificada (no período das cheias) é de 3800 l/s. Em decorrência de problemas de nível d’água na linha de sucção da estação de bombeamento, durante a época da estiagem, construiu-se à jusante do ponto de captação uma pequena barragem cujo vertedor de 3 m de soleira tem a forma de um perfil padrão WES, que foi desenhado para uma carga de projeto hd =0,50 m. Para o bom funcionamento das bombas, o nível mínimo d’água no ponto de captação deverá estar na cota de 100,00 m, conforme a Figura 12.51. Nestas condições, pergunta-se: a) Em que cota estará a crista do vertedor-extravasor? André Barcellos Ferreira – andrepoetta@hotmail.com 37 Universidade Federal do Espírito Santo b) Durante a época das enchentes, qual será a máxima cota do nível d’água? 3/2 0,148 0,5 m WES: 3,0 m 2,215750 250 450 l/s d d Q C L hh Vertedor L hCQ h = ⋅ ⋅= ∗ = = = − = Sendo h a carga de trabalho, então: a) 0,148 0,148 3/2 3/2 1,6480,45 0,50,45 2,215 3 0,183 0,5 3 2,215 hQ C L h h h h⋅ = ⋅ ⋅ ⇒ = ⋅ ⋅ ⋅ ⇔ = ⇔ = ⋅ m 100 m N 99,817 mcrista cristaN h∴ + = ⇔ = b) Vazão = 3.800 l/s – 250 l/s = 3550 l/s 0,148 0,148 3/2 1,6483,55 0,53,55 2,215 3 0,642 m 0,5 3 2,215 NA ' 99,817 0,642 100,459 mmáx c máx h h h h N h NA ⋅ = ⋅ ⋅ ⋅ ⇔ = ⇔ = ⋅ ∴ = + = + ⇒ = .









