
Elementos solicitados com cargas axiais
UNIVERSIDAD E FEDERAL DO RIO GRANDE DO NORTE
DEPARTAMENTO DE ENGENHARIA CIVIL E AMBIENTAL
CENTRO DE TECNOLOGIA
Prof.(a): Yngrid Rayane Freitas do Nascimento
CIV0411 - Resistência dos Materiais I
CIV 0411 – Resistência dos Materiais I
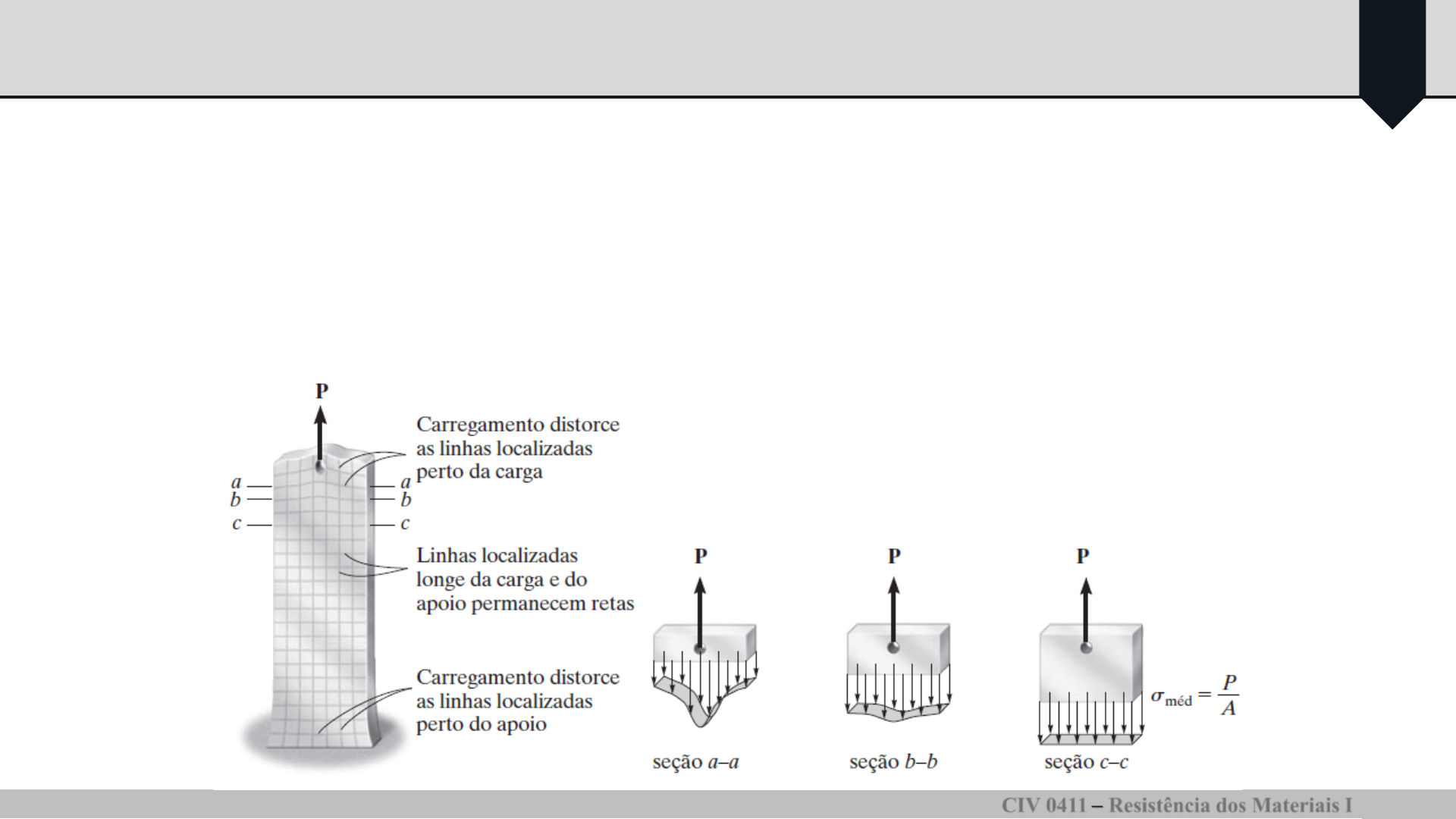
Princípio de Saint-Venant
•A deformação localizada que ocorre nas regiões próximas ao ponto de aplicação tende
a diminuir conforme as medições são feitas cada vez mais distante das extremidades.
•Admite-se que à uma distância (mínima) igual a maior dimensão da seção transversal
carregada, esses efeitos podem ser desprezados.
CIV 0411 – Resistência dos Materiais I
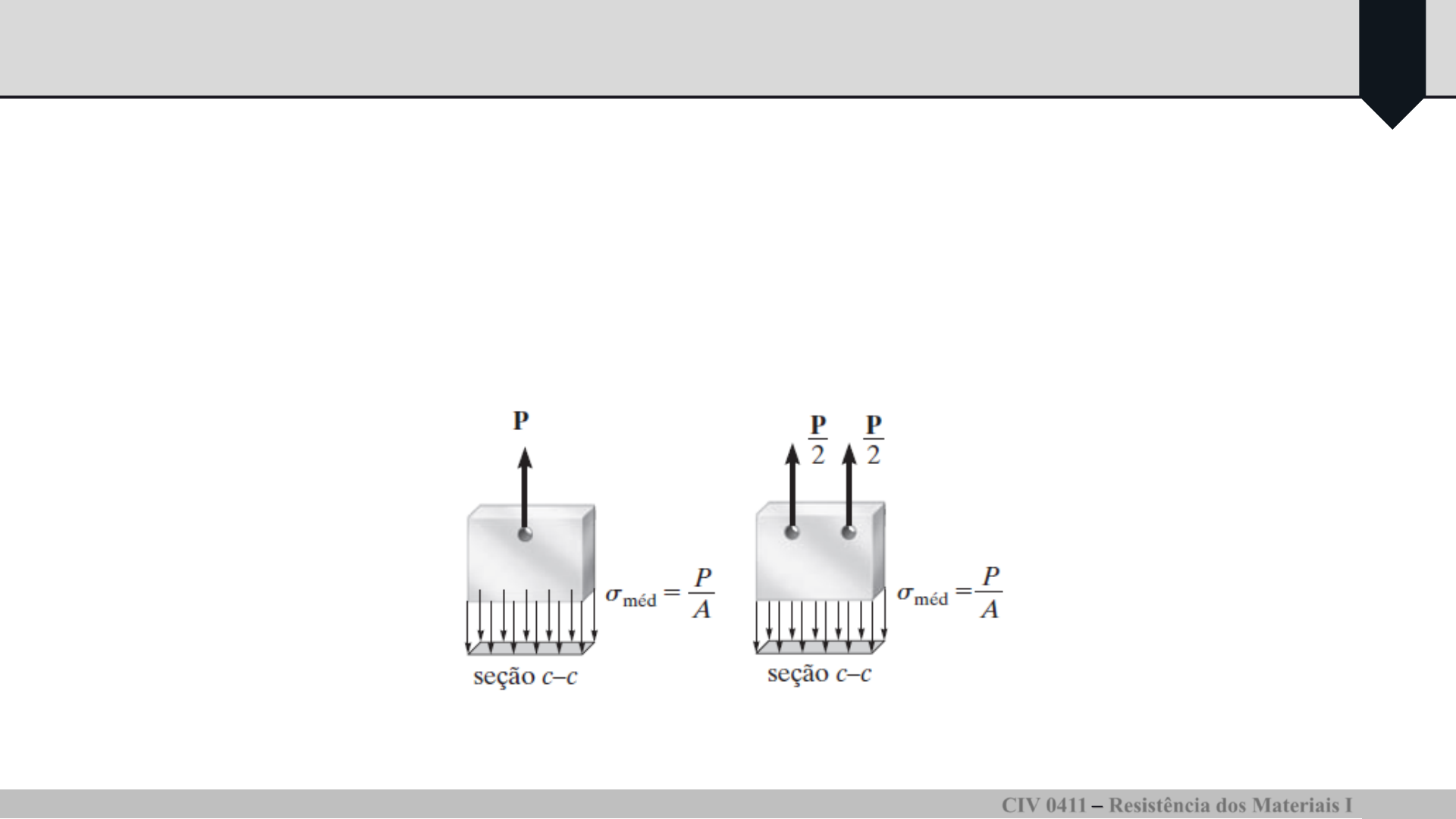
Princípio de Saint-Venant
A tensão e a deformação produzidas em pontos de um corpo suficientemente distantes
da região da aplicação da carga serão iguais à tensão e à deformação produzidas por
quaisquer carregamentos aplicados que tenham a mesma resultante estaticamente
equivalente e sejam aplicados ao corpo dentro da mesma região.
CIV 0411 – Resistência dos Materiais I
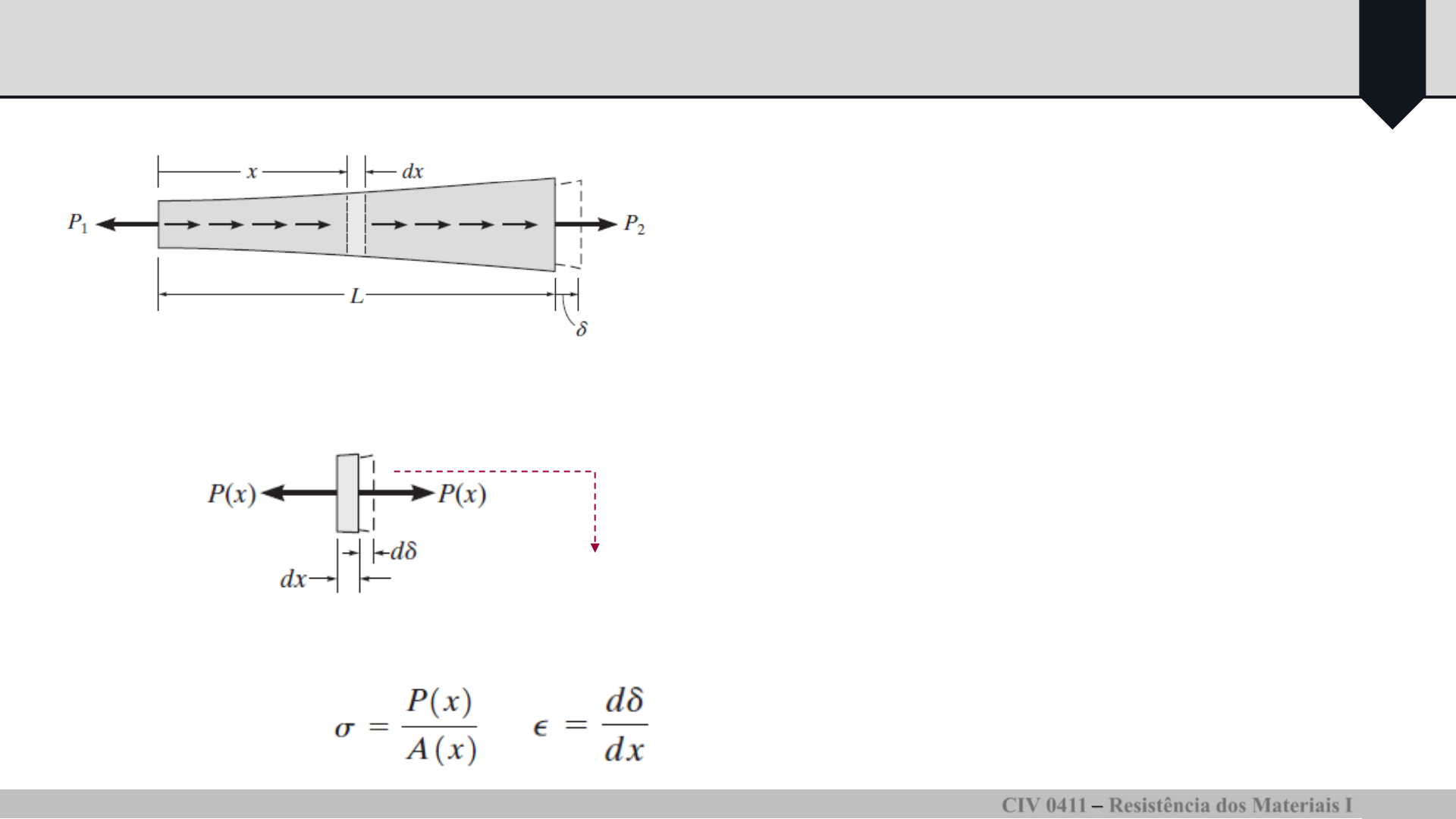
Deformação elástica de um elemento submetido a carga axial
•A área de seção transversal varia
gradativamente ao longo de seu
comprimento L.
•A barra está sujeita a cargas concentradas
em suas extremidades e a uma carga
externa variável distribuída ao longo de seu
comprimento.
Área da seção: A(x)
Diagrama de corpo livre do elemento
de comprimento dx
Tensão e deformação no elemento:
CIV 0411 – Resistência dos Materiais I
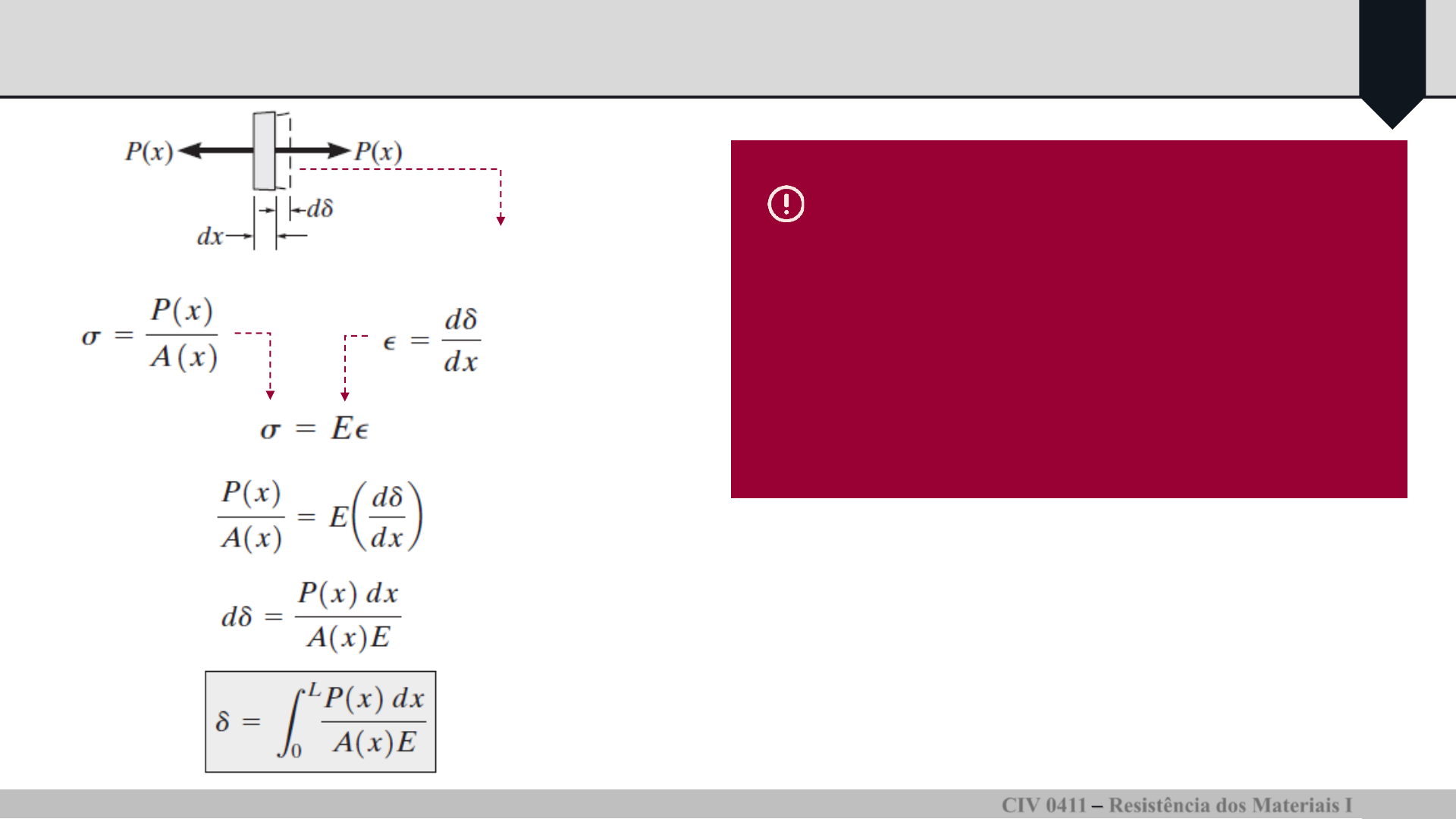
Deformação elástica de um elemento submetido a carga axial
Área da seção: A(x)
Relembrando: A relação matemática
entre tensão e deformação depende do tipo de
material do qual o corpo é feito.
Se o material se comportar de maneira linear
elástica, a lei de Hooke será aplicável e
haverá uma relação prop orcional entre tensão
e deformação.
Onde:
: deslocamento de um po nto na barra relativo a um outro ponto ;
L: distân cia original entre os ponto s;
P(x): força axial inte rna na s eção, lo calizada a dist ância x de u ma
extremidade ;
A(x): área da seção transv ersal da barra, exp ressa em fun ção de x;
E: módu lo de elasticidade para o material
CIV 0411 – Resistência dos Materiais I
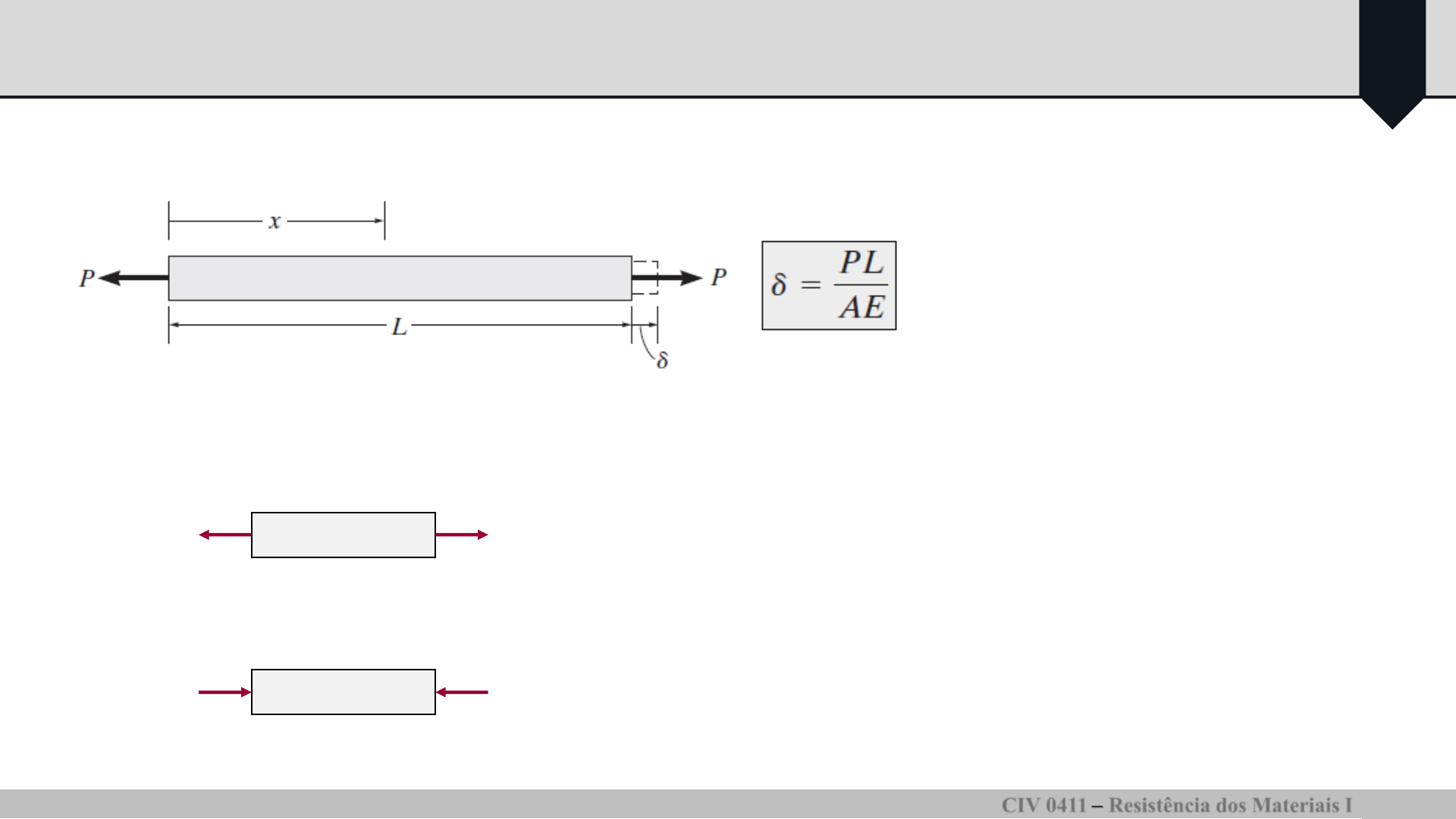
Deformação elástica de um elemento submetido a carga axial
Carga e área de seção transversal constantes.
Atenção! Se a carga axial, a área da
seção transversal ou o material da
seção variar de um trecho para o
outro, a equação acima poderá ser
aplicada a cada segmento da barra
onde todas essas quantidades são
constantes.
Convenção de sinais
TRAÇÃO
COMPRESSÃO
Alongamentos são considerados positivos
Encurtamentos são considerados negativos

CIV 0411 – Resistência dos Materiais I
Deformação elástica de um elemento submetido a carga axial
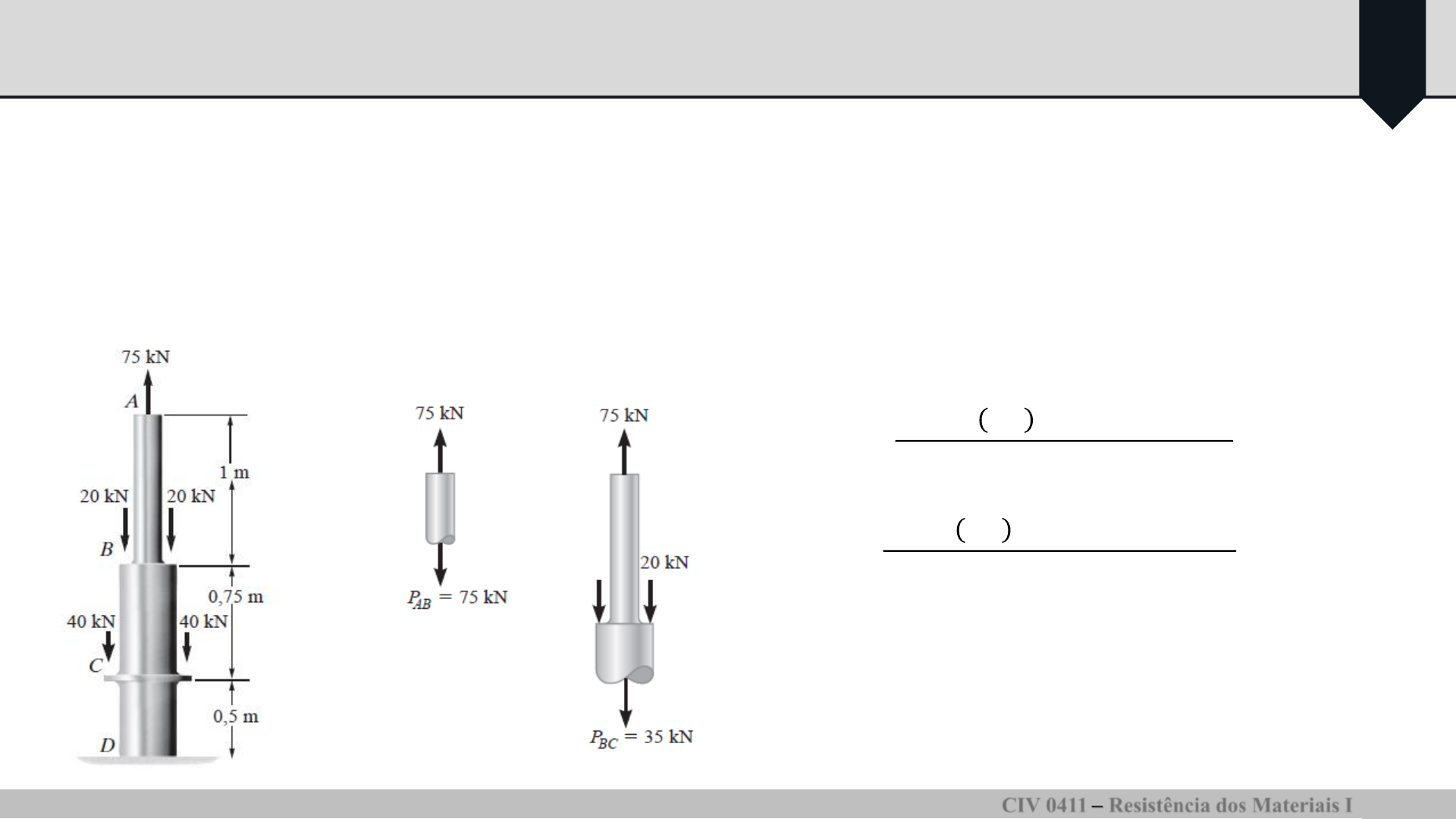
Exemplo 1: A barra de aço A-36 mostrada na Figura é composta por do is segmentos, AB e BD,
com áreas de seção transversal
e , respectivamente.
Determine o deslocamento vertical da extremidade A e o deslocamento de B em relação a C.
Considere
GPa.
CIV 0411 – Resistência dos Materiais I
Deformação elástica de um elemento submetido a carga axial
Exemplo 1: A barra de aço A-36 mostrada na Figura é composta por do is segmentos, AB e BD,
com áreas de seção transversal
e , respectivamente.
Determine o deslocamento vertical da extremidade A e o deslocamento de B em relação a C.
Considere
GPa.
Trecho AB:
Trecho BC:
CIV 0411 – Resistência dos Materiais I
Deformação elástica de um elemento submetido a carga axial
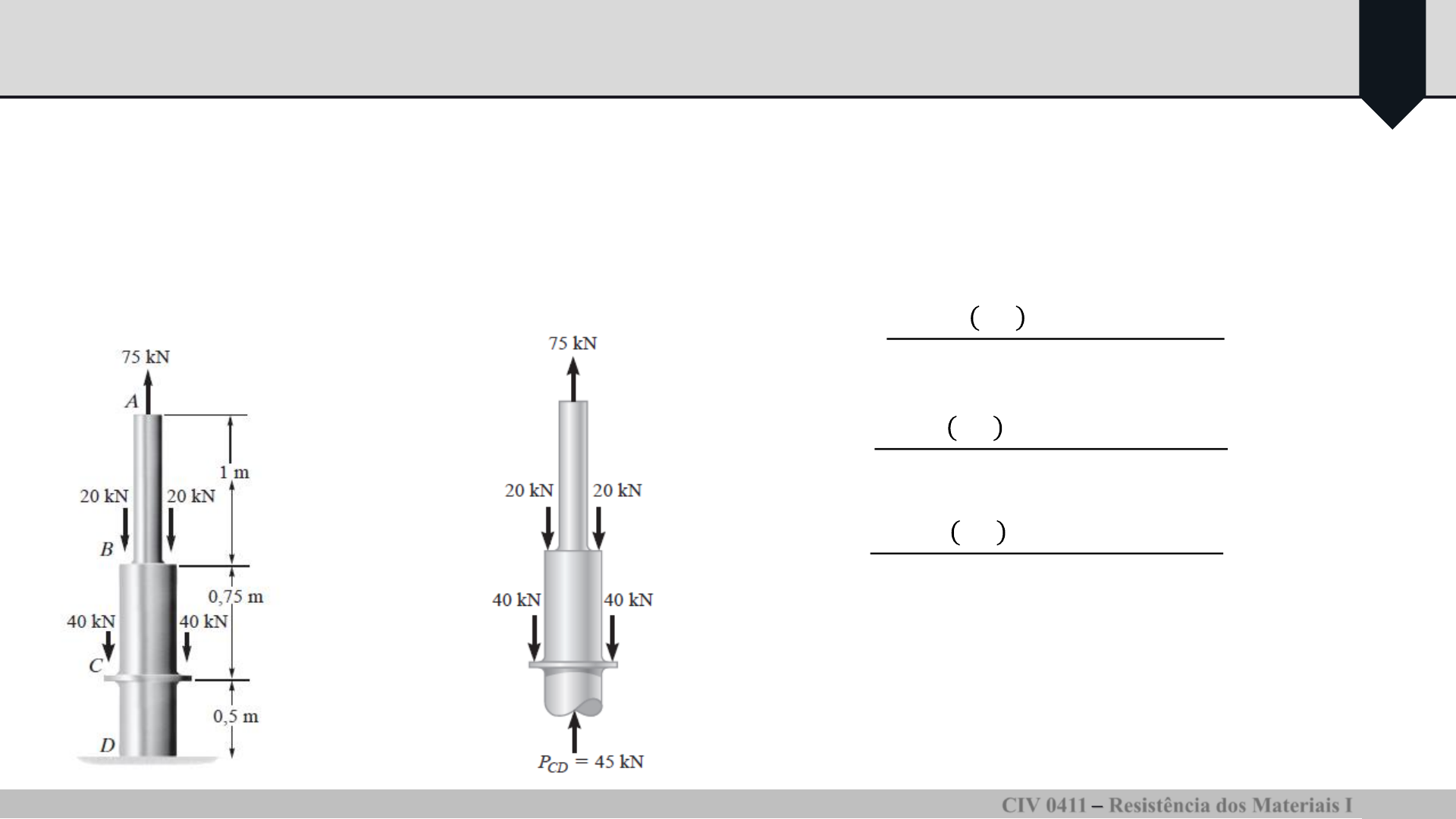
Exemplo 1: A barra de aço A-36 mostrada na Figura é composta por do is segmentos, AB e BD,
com áreas de seção transversal
e , respectivamente.
Determine o deslocamento vertical da extremidade A e o deslocamento de B em relação a C.
Considere
GPa.
Trecho CD:
CIV 0411 – Resistência dos Materiais I
Deformação elástica de um elemento submetido a carga axial
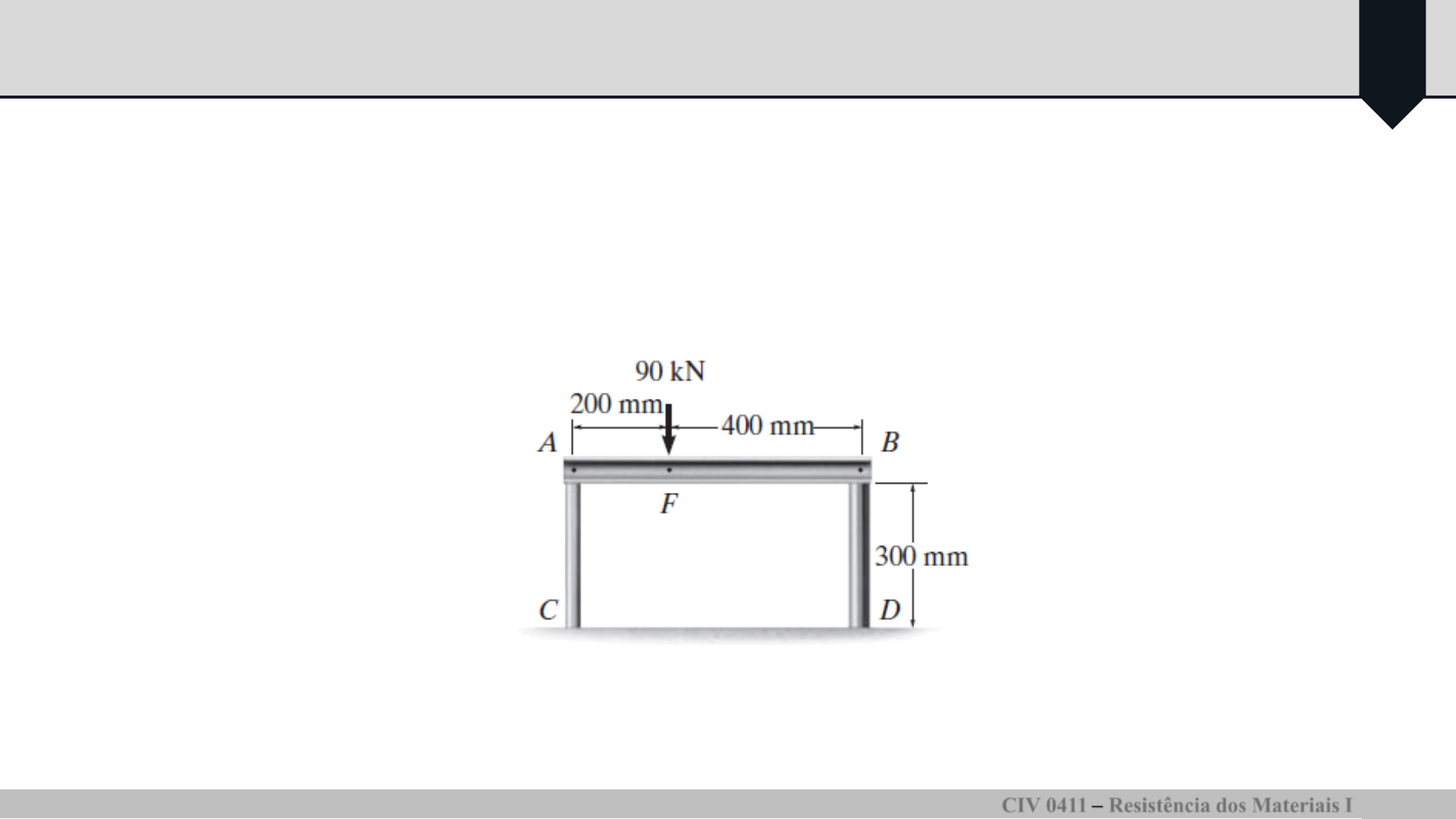
Exemplo 2: Uma viga rígida AB está apoiada nos dois postes curtos mostrados na Figura. AC é
feito de aço e tem diâmetro de 20 mm, e BD é feito de alumínio e te m diâmetro de 40 mm.
Determine o deslocamento do ponto F em AB se uma carga vertic al de 90 kN for aplicada nesse
ponto. Considere
GPa,
GPa.
Prévia do material em texto
Elementos solicitados com cargas axiais UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE DEPARTAMENTO DE ENGENHARIA CIVIL E AMBIENTAL CENTRO DE TECNOLOGIA Prof.(a): Yngrid Rayane Freitas do Nascimento CIV0411 - Resistência dos Materiais I CIV 0411 – Resistência dos Materiais I Princípio de Saint-Venant • A deformação localizada que ocorre nas regiões próximas ao ponto de aplicação tende a diminuir conforme as medições são feitas cada vez mais distante das extremidades. • Admite-se que à uma distância (mínima) igual a maior dimensão da seção transversal carregada, esses efeitos podem ser desprezados. CIV 0411 – Resistência dos Materiais I Princípio de Saint-Venant A tensão e a deformação produzidas em pontos de um corpo suficientemente distantes da região da aplicação da carga serão iguais à tensão e à deformação produzidas por quaisquer carregamentos aplicados que tenham a mesma resultante estaticamente equivalente e sejam aplicados ao corpo dentro da mesma região. CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial • A área de seção transversal varia gradativamente ao longo de seu comprimento L. • A barra está sujeita a cargas concentradas em suas extremidades e a uma carga externa variável distribuída ao longo de seu comprimento. Área da seção: A(x) Diagrama de corpo livre do elemento de comprimento dx Tensão e deformação no elemento: CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial Área da seção: A(x) Relembrando: A relação matemática entre tensão e deformação depende do tipo de material do qual o corpo é feito. Se o material se comportar de maneira linear elástica, a lei de Hooke será aplicável e haverá uma relação proporcional entre tensão e deformação. Onde: 𝛿: deslocamento de um ponto na barra relativo a um outro ponto; L: distância original entre os pontos; P(x): força axial interna na seção, localizada a distância x de uma extremidade; A(x): área da seção transversal da barra, expressa em função de x; E: módulo de elasticidade para o material CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial Carga e área de seção transversal constantes. Atenção! Se a carga axial, a área da seção transversal ou o material da seção variar de um trecho para o outro, a equação acima poderá ser aplicada a cada segmento da barra onde todas essas quantidades são constantes. Convenção de sinais TRAÇÃO COMPRESSÃO Alongamentos são considerados positivos Encurtamentos são considerados negativos CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial Exemplo 1: A barra de aço A-36 mostrada na Figura é composta por dois segmentos, AB e BD, com áreas de seção transversal 𝐴𝐴𝐵 = 600 𝑚𝑚2 e 𝐴𝐵𝐷 = 1.200 𝑚𝑚2 , respectivamente. Determine o deslocamento vertical da extremidade A e o deslocamento de B em relação a C. Considere 𝐸𝑎ç𝑜 = 210 GPa. CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial Exemplo 1: A barra de aço A-36 mostrada na Figura é composta por dois segmentos, AB e BD, com áreas de seção transversal 𝐴𝐴𝐵 = 600 𝑚𝑚2 e 𝐴𝐵𝐷 = 1.200 𝑚𝑚2 , respectivamente. Determine o deslocamento vertical da extremidade A e o deslocamento de B em relação a C. Considere 𝐸𝑎ç𝑜 = 210 GPa. Trecho AB: 𝛿𝐴𝐵 = +75 𝑘𝑁 ∙ 1 ∙ 103(𝑚𝑚) 600 (𝑚𝑚2) ∙ 210 ( Τ𝑘𝑁 𝑚𝑚2) = +0,595 𝑚𝑚 1 𝐺𝑃𝑎 = 103𝑀𝑃𝑎 1 𝑀𝑃𝑎 = 10−3 𝑘𝑁/𝑚𝑚2Trecho BC: 𝛿𝐵𝐶 = +35 𝑘𝑁 ∙ 0,75 ∙ 103(𝑚𝑚) 1200 (𝑚𝑚2) ∙ 210 ( Τ𝑘𝑁 𝑚𝑚2) = +0,104 𝑚𝑚 CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial Exemplo 1: A barra de aço A-36 mostrada na Figura é composta por dois segmentos, AB e BD, com áreas de seção transversal 𝐴𝐴𝐵 = 600 𝑚𝑚2 e 𝐴𝐵𝐷 = 1.200 𝑚𝑚2 , respectivamente. Determine o deslocamento vertical da extremidade A e o deslocamento de B em relação a C. Considere 𝐸𝑎ç𝑜 = 210 GPa. Trecho CD: 𝛿𝐴𝐵 = +75 𝑘𝑁 ∙ 1 ∙ 103(𝑚𝑚) 600 (𝑚𝑚2) ∙ 210 ( Τ𝑘𝑁 𝑚𝑚2) = +0,595 𝑚𝑚 𝛿𝐵𝐶 = +35 𝑘𝑁 ∙ 0,75 ∙ 103(𝑚𝑚) 1200 (𝑚𝑚2) ∙ 210 ( Τ𝑘𝑁 𝑚𝑚2) = +0,104 𝑚𝑚 𝛿𝐶𝐷 = −45 𝑘𝑁 ∙ 0,5 ∙ 103(𝑚𝑚) 1200 (𝑚𝑚2) ∙ 210 ( Τ𝑘𝑁 𝑚𝑚2) = −0,089 𝑚𝑚 𝛿𝐴𝐷 = +0,595 𝑚𝑚 + 0,104 𝑚𝑚 − 0,089 𝑚𝑚 = 0,61 𝑚𝑚 CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial Exemplo 2: Uma viga rígida AB está apoiada nos dois postes curtos mostrados na Figura. AC é feito de aço e tem diâmetro de 20 mm, e BD é feito de alumínio e tem diâmetro de 40 mm. Determine o deslocamento do ponto F em AB se uma carga vertical de 90 kN for aplicada nesse ponto. Considere 𝐸𝑎ç𝑜 = 200 GPa, 𝐸𝑎𝑙 = 70 GPa. CIV 0411 – Resistência dos Materiais I Deformação elástica de um elemento submetido a carga axial Exemplo 2: Uma viga rígida AB está apoiada nos dois postes curtos mostrados na Figura. AC é feito de aço e tem diâmetro de 20 mm, e BD é feito de alumínio e tem diâmetro de 40 mm. Determine o deslocamento do ponto F em AB se uma carga vertical de 90 kN for aplicada nesse ponto. Considere 𝐸𝑎ç𝑜 = 200 GPa, 𝐸𝑎𝑙 = 70 GPa. 𝛿𝐴𝐶 = −60 𝑘𝑁 ∙ 300(𝑚𝑚) 102𝜋 (𝑚𝑚2) ∙ 200 ( Τ𝑘𝑁 𝑚𝑚2) = −0,286 𝑚𝑚 𝛿𝐵𝐷 = −30 𝑘𝑁 ∙ 300(𝑚𝑚) 202𝜋 (𝑚𝑚2) ∙ 70 ( Τ𝑘𝑁 𝑚𝑚2) = −0,102 𝑚𝑚 CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado ∑𝐹𝑦 = 0 ∴ 𝐹𝐴 = 𝑃 ∑𝐹𝑦 = 0 ∴ 𝐹𝐴 + 𝐹𝐵 − 𝑃 = 0 Estaticamente determinado Estaticamente indeterminado Condição de compatibilidade ou condição cinemática. 𝛿𝐴𝐵 = 0 Condições de compatibilidade especificam as restrições ao deslocamento que ocorrem nos apoios ou em outros pontos de um elemento. CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado ∑𝐹𝑦 = 0 𝐹𝐴 + 𝐹𝐵 − 𝑃 = 0 Estaticamente indeterminado 𝛿𝐴𝐵 = 0 Alongamento Encurtamento Considerando que AE é constante: CIV 0411 – Resistência dos Materiais I Princípio da superposição 1. A carga deve estar relacionada linearmente com a tensão ou o deslocamento a ser determinado. 2. A carga não deve provocar mudanças significativas na geometria ou configuração original do elemento Comportamento Linear-Elástico Simplificação do carregamento + Sobreposição dos efeitos CIV 0411 – Resistência dos Materiais I Método de análise de força para elementos carregados axialmente Estaticamente indeterminado Liberação temporária de um dos vínculos Se a carga P provocar um deslocamento 𝛿𝑃 para baixo em B, a reação 𝑭𝐵 deve provocar um deslocamento equivalente 𝛿𝐵 para cima na extremidade B, de modo que não ocorra nenhum deslocamento em B quando as duas cargas forem superpostas. CIV 0411 – Resistência dos Materiais I Método de análise de força para elementos carregados axialmente Estaticamente indeterminado Liberação temporária de um dos vínculos Compatibilidade: ∴ Equilíbrio: ∴ CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado Exemplo 3: O poste de alumínio mostrado na Figura é reforçado com um núcleo de latão. Se esse conjunto suportar uma carga de compressão axial resultante P = 45 kN, aplicada na tampa rígida, determine a tensão normal média no alumínio e no latão. Considere 𝐸𝑎𝑙 = 70 ∙ (103) MPa e 𝐸𝑙𝑎𝑡 = 105 ∙ (103) MPa. D.C.L. CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado Exemplo 3: O poste de alumínio mostrado na Figura é reforçado com um núcleo de latão. Se esse conjunto suportar uma carga de compressão axial resultante P = 45 kN, aplicada na tampa rígida, determine a tensão normal média no alumínio e no latão. Considere 𝐸𝑎𝑙 = 70 ∙ (103) MPa e 𝐸𝑙𝑎𝑡 = 105 ∙ (103) MPa. A tampa rígida na parte superior do poste obriga que o deslocamento de ambos,alumínio e latão, seja o mesmo. Portanto, ∴ CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado Exemplo 3: O poste de alumínio mostrado na Figura é reforçado com um núcleo de latão. Se esse conjunto suportar uma carga de compressão axial resultante P = 45 kN, aplicada na tampa rígida, determine a tensão normal média no alumínio e no latão. Considere 𝐸𝑎𝑙 = 70 ∙ (103) MPa e 𝐸𝑙𝑎𝑡 = 105 ∙ (103) MPa. CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado Exemplo 4: As três barras de aço A-36 mostradas na Figura estão conectadas por pinos a um elemento rígido. Se a carga aplicada ao elemento for 15 kN, determine a força desenvolvida em cada barra. Cada uma das barras AB e EF tem área de seção transversal de 25 mm², e a barra CD tem área de seção transversal de 15 mm². D.C.L. do elemento rígido CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado Exemplo 4: As três barras de aço A-36 mostradas na Figura estão conectadas por pinos a um elemento rígido. Se a carga aplicada ao elemento for 15 kN, determine a força desenvolvida em cada barra. Cada uma das barras AB e EF tem área de seção transversal de 25 mm², e a barra CD tem área de seção transversal de 15 mm². D.C.L. do elemento rígido CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado Exemplo 5: A haste de aço A-36 mostrada na Figura tem diâmetro de 5 mm. Ela está presa à parede fixa em A e, antes de ser carregada, há uma folga de 1 mm entre a parede em B’ e a haste. Determine as reações em A e B’. CIV 0411 – Resistência dos Materiais I Elemento com carga axial estaticamente indeterminado Exemplo 5: A haste de aço A-36 mostrada na Figura tem diâmetro de 5 mm. Ela está presa à parede fixa em A e, antes de ser carregada, há uma folga de 1 mm entre a parede em B’ e a haste. Determine as reações em A e B’. Compatibilidade: CIV 0411 – Resistência dos Materiais I em que 𝛼 é uma constante característica do material, chamada de coeficiente de dilatação térmica. Com a deformação 𝑑𝑇 deve ser associada uma deformação específica 𝜖𝑇 = 𝛿𝑇/𝐿. Não há tensão associada com a deformação específica 𝜖𝑇. Problemas que envolvem mudanças de temperatura CIV 0411 – Resistência dos Materiais I Condição inicial: ∆𝑇° 𝜖𝑇 = 𝛿𝑇 𝐿 = 0 Variação de temperatura: Liberação do vínculo em B para análise: Compatibilidade de deformações Aplica-se somente no caso de uma barra homogênea de seção transversal uniforme Problemas que envolvem mudanças de temperatura − − CIV 0411 – Resistência dos Materiais I Problemas que envolvem mudanças de temperatura Exemplo 6: Determine os valores da tensão nas partes AC e CB da barra de aço mostrada quando a temperatura da barra for de -45° C, sabendo que ambos os apoios rígidos estão ajustados quando a temperatura estiver a 20 °C. Use os valores 𝐸 = 200 GPa e 𝛼 = 12 × 10−6/°𝐶 para o aço. CIV 0411 – Resistência dos Materiais I Problemas que envolvem mudanças de temperatura Exemplo 6: Determine os valores da tensão nas partes AC e CB da barra de aço mostrada quando a temperatura da barra for de -45° C, sabendo que ambos os apoios rígidos estão ajustados quando a temperatura estiver a 20 °C. Use os valores 𝐸 = 200 GPa e 𝛼 = 12 × 10−6/°𝐶 para o aço. Deformação correspondente a ∆𝑻°𝑪 CIV 0411 – Resistência dos Materiais I Problemas que envolvem mudanças de temperatura Exemplo 6: Determine os valores da tensão nas partes AC e CB da barra de aço mostrada quando a temperatura da barra for de -45° C, sabendo que ambos os apoios rígidos estão ajustados quando a temperatura estiver a 20 °C. Use os valores 𝐸 = 200 GPa e 𝛼 = 12 × 10−6/°𝐶 para o aço. Deformação correspondente a ∆𝑻°𝑪 Deformação correspondente a reação em B CIV 0411 – Resistência dos Materiais I Problemas que envolvem mudanças de temperatura Exemplo 6: Determine os valores da tensão nas partes AC e CB da barra de aço mostrada quando a temperatura da barra for de -45° C, sabendo que ambos os apoios rígidos estão ajustados quando a temperatura estiver a 20 °C. Use os valores 𝐸 = 200 GPa e 𝛼 = 12 × 10−6/°𝐶 para o aço. Compatibilidade de deformações Tensões normais CIV 0411 – Resistência dos Materiais I Problemas que envolvem mudanças de temperatura Exemplo 6: Determine os valores da tensão nas partes AC e CB da barra de aço mostrada quando a temperatura da barra for de -45° C, sabendo que ambos os apoios rígidos estão ajustados quando a temperatura estiver a 20 °C. Use os valores 𝐸 = 200 GPa e 𝛼 = 12 × 10−6/°𝐶 para o aço. Deformação específica (trecho AC) Deformação específica (trecho BC) CIV 0411 – Resistência dos Materiais I Problemas que envolvem mudanças de temperatura Exemplo 6: Determine os valores da tensão nas partes AC e CB da barra de aço mostrada quando a temperatura da barra for de -45° C, sabendo que ambos os apoios rígidos estão ajustados quando a temperatura estiver a 20 °C. Use os valores 𝐸 = 200 GPa e 𝛼 = 12 × 10−6/°𝐶 para o aço. Deformações por trecho: Embora a soma 𝛿 = 𝛿𝐴𝐶 + 𝛿𝐶𝐵 das duas deformações seja zero, nenhuma das deformações é igual a zero. REFERÊNCIAS BEER, F. P.; JOHNSTON, E. R.; DEWOLF, J. T.; MAZUREK, D. F. Mecânica dos materiais. 5 ed. Porto Alegre: AMGH, 2011; HIBBELER, R. C. Resistência dos Materiais. 7 ed. São Paulo : Pearson Prentice Hall, 2010. Yngrid Rayane Freitas do Nascimento yngrid.rayane.eng@gmail.com Slide 1 Slide 2 Slide 3 Slide 4 Slide 5 Slide 6 Slide 7 Slide 8 Slide 9 Slide 10 Slide 11 Slide 12 Slide 13 Slide 14 Slide 15 Slide 16 Slide 17 Slide 18 Slide 19 Slide 20 Slide 21 Slide 22 Slide 23 Slide 24 Slide 25 Slide 26 Slide 27 Slide 28 Slide 29 Slide 30 Slide 31 Slide 32







