multiplicação
Método da chave
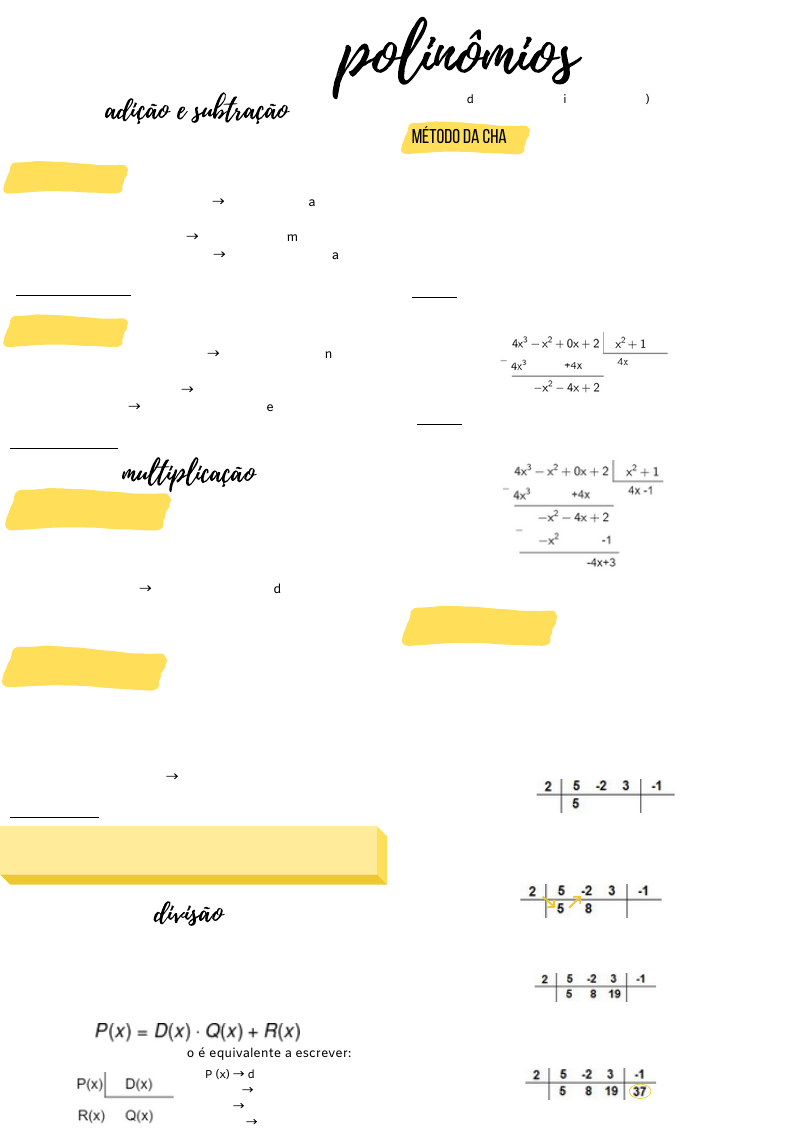
Consiste em realizar a divisão entre polinômios seguindo
amesma ideia da divisão entre dois números, o
chamadoalgoritmo da divisão.
Veja o exemplo a seguir:
Novamente vamos considerar os polinômios
P (x) = 4x3– x2+ 2 e D (x) = x2+ 1,
e agora vamos dividi-los utilizando o método da chave.
Passo 1- Dividir o primeiro termo do dividendo pelo primeiro
termo do divisor e, em seguida, multiplicar o quociente por
todo divisor.
Veja:
polinômio por polinômio
Veja o exemplo:
P1:(x – 1); P2:(x2+ 2x - 6)
P1xP2
x2(x – 1) + 2x * (x – 1) – 6 * (x – 1)
(x³ – x²) + (2x² – 2x) – (6x – 6)
x³ – x² + 2x² – 2x – 6x + 6
→
reduzindo os termos
semelhantes.
x³ + x² – 8x + 6
Portanto, nas multiplicações entre monômios e polinômios
aplicamos a propriedade distributiva da multiplicação.
Considere os polinômios P1: –2x² + 5x – 2e P2: –3x³ + 2x -1
adição (P1+P2)
(–2x² + 5x – 2) + (–3x³ + 2x – 1)
→
eliminar os parênteses
realizando o jogo de sinal
–2x² + 5x – 2 – 3x³ + 2x – 1
→
reduzir os termos
semelhantes–2x² + 7x – 3x³ – 3
→
ordenar de forma
decrescente de acordo com a potência
–3x³ – 2x² + 7x – 3
Método Briot-Ruffini
Utilizado paradividir polinômios por binômios.
Vamos considerar os polinômios:
P(x) = 5x3– 2x2+ 3x – 1eQ(x) = x – 2
Esse método consiste em desenhar dois segmentos, um
horizontal e outro vertical, e nesses segmentos colocamos o
coeficiente do dividendo e a raiz do polinômio divisor, além
disso, repete-se o primeiro coeficiente.
Veja:
x+
Subtração (p1-p2)
(–2x² + 5x – 2) – (–3x³ + 2x – 1)
→
eliminar os parênteses
realizando o jogo de sinal
–2x² + 5x – 2 + 3x³ – 2x + 1
→
reduzir os termos semelhantes
–2x² + 3x – 1 + 3x³
→
ordenar de forma decrescente de
acordo com a potência
3x³ – 2x² + 3x – 1
polinômio por monômio
observe o exemplo:
P1: (3x²); P2:(5x³ + 8x² – x)
P1xP2
(3x²) * (5x³ + 8x² – x)
→
aplicar a propriedade distributiva da
multiplicação
15x⁵ + 24x⁴ – 3x³
POLINÔMIOS
Ao dividir um polinômio P (x) por um polinômio D
(x) não nulo, em que o grau de P é maior que D
(P>D), quer dizer que devemos encontrar um
polinômio Q (x) e R (x),
de modo que:
Passo 2-Dividir o resto do passo 2 pelo quociente e repetir
esse processo até que o grau do resto seja menor que o grau
do quociente.
polinômios
adição e subtração
divisão
Note que esse processo é equivalente a escrever:
P (x)
→
dividendo
D (x)
→
divisor
Q (x)
→
quociente
R (x)
→
resto
quando o resto da divisão entre P (x) e D (x) é igual a zero,
dizemos que P (x) édivisívelpor D (x).
Logo, Q (x) = 4x-1 e R (x) = -4x +3.
raiz:
Q(x) = 0
x – 2 = 0
x= 2
Agora nós multiplicamos o5por2e somamos o resultado com o
segundo coeficiente de P(x), o número– 2, isto é, fazemos5.2 + (– 2) = 8.
O resultado8deve ser escrito embaixo do coeficiente– 2.
Repetimos o processo, multiplicamos8por2e somamos com o terceiro
coeficiente de P(x), o número3. O cálculo é dado por8.2 + 3 = 19.
Escrevemos o resultado embaixo do coeficiente3.
Repetimos o procedimento pela última vez. Agora multiplicamos o19por 2
e somamos o resultado com– 1, ou seja, nós fazemos19.2 + (– 1) = 37. O
resultado37é colocado embaixo de –1e é orestode nossa divisão.
=R(x)
@hwurricane

O polinômio resultante dessa divisão é determinado pelos
números5, 8e19. Estes são coeficientes desse polinômio. Como
fora dito anteriormente, o último número (19) é acompanhado
dex0,o8é acompanhado dex1, e o5é acompanhado dex2.
Portanto, o polinômio resultante da divisão é5x2+ 8x + 19, e o
resto da divisão ér = 37.
teorema de d'alembert
é uma consequência imediata do teorema do resto, que são
voltados para a divisão de polinômio por binômio do tipo x – a.
O teorema do resto diz que um polinômio G(x) dividido por um
binômio x – a terá resto R igual a P(a), para x = a.
O matemático francês D’Alembert provou, levando em
consideração o teorema citado acima, que um polinômio
qualquer Q(x) será divisível por x – a, ou seja, o resto da
divisão será igual à zero (R = 0) se P(a) = 0.
Esse teorema facilitou o cálculo da divisão de polinômio por
binômio (x –a), dessa forma não sendo preciso resolver toda a
divisão para saber se o resto é igual ou diferente de zero.
Exemplo 1
Calcule o resto da divisão (x² + 3x – 10) : (x – 3).
Como diz o Teorema de D’Alembert, o resto (R) dessa divisão
será igual a:
P(3) = R
3² + 3 * 3 – 10 = R
9 + 9 – 10 = R
18 – 10 = R
R = 8
Portanto, o resto dessa divisão será 8.
Exemplo 2
Calcule o resto da divisão do polinômio 3x3+ x2– 6x + 7 por
2x + 1.
R = P(x)
→
R = P(– 1/2)
R = 3*(–1/2)³ + (–1/2)² – 6*(–1/2) + 7
R = 3*(–1/8) + 1/4 + 3 + 7
R = –3/8 + 1/4 + 10 (mmc)
R = –3/8 + 2/8 + 80/8
R = 79/8
raiz:
Q(x) = 0
x – 3 = 0
x= 3
@hwurricane
Prévia do material em texto
multiplicação Método da chave Consiste em realizar a divisão entre polinômios seguindo a mesma ideia da divisão entre dois números, o chamado algoritmo da divisão. Veja o exemplo a seguir: Novamente vamos considerar os polinômios P (x) = 4x3 – x2 + 2 e D (x) = x2 + 1, e agora vamos dividi-los utilizando o método da chave. Passo 1 - Dividir o primeiro termo do dividendo pelo primeiro termo do divisor e, em seguida, multiplicar o quociente por todo divisor. Veja: polinômio por polinômio Veja o exemplo: P1:(x – 1); P2:(x2 + 2x - 6) P1xP2 x2 (x – 1) + 2x * (x – 1) – 6 * (x – 1) (x³ – x²) + (2x² – 2x) – (6x – 6) x³ – x² + 2x² – 2x – 6x + 6 → reduzindo os termos semelhantes. x³ + x² – 8x + 6 Portanto, nas multiplicações entre monômios e polinômios aplicamos a propriedade distributiva da multiplicação. Considere os polinômios P1: –2x² + 5x – 2 e P2: –3x³ + 2x -1 adição (P1+P2) (–2x² + 5x – 2) + (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal –2x² + 5x – 2 – 3x³ + 2x – 1 → reduzir os termos semelhantes–2x² + 7x – 3x³ – 3 → ordenar de forma decrescente de acordo com a potência –3x³ – 2x² + 7x – 3 Método Briot-Ruffini Utilizado para dividir polinômios por binômios. Vamos considerar os polinômios: P(x) = 5x3 – 2x2 + 3x – 1 e Q(x) = x – 2 Esse método consiste em desenhar dois segmentos, um horizontal e outro vertical, e nesses segmentos colocamos o coeficiente do dividendo e a raiz do polinômio divisor, além disso, repete-se o primeiro coeficiente. Veja: x + Subtração (p1-p2) (–2x² + 5x – 2) – (–3x³ + 2x – 1) → eliminar os parênteses realizando o jogo de sinal –2x² + 5x – 2 + 3x³ – 2x + 1 → reduzir os termos semelhantes –2x² + 3x – 1 + 3x³ → ordenar de forma decrescente de acordo com a potência 3x³ – 2x² + 3x – 1 polinômio por monômio observe o exemplo: P1: (3x²); P2:(5x³ + 8x² – x) P1xP2 (3x²) * (5x³ + 8x² – x) → aplicar a propriedade distributiva da multiplicação 15x⁵ + 24x⁴ – 3x³ POLINÔMIOS Ao dividir um polinômio P (x) por um polinômio D (x) não nulo, em que o grau de P é maior que D (P > D), quer dizer que devemos encontrar um polinômio Q (x) e R (x), de modo que: Passo 2 - Dividir o resto do passo 2 pelo quociente e repetir esse processo até que o grau do resto seja menor que o grau do quociente. polinômios adição e subtração divisão Note que esse processo é equivalente a escrever: P (x) → dividendo D (x) → divisor Q (x) → quociente R (x) → resto quando o resto da divisão entre P (x) e D (x) é igual a zero, dizemos que P (x) é divisível por D (x). Logo, Q (x) = 4x-1 e R (x) = -4x +3. raiz: Q(x) = 0 x – 2 = 0 x= 2 Agora nós multiplicamos o 5 por 2 e somamos o resultado com o segundo coeficiente de P(x), o número – 2, isto é, fazemos 5.2 + (– 2) = 8. O resultado 8 deve ser escrito embaixo do coeficiente – 2. Repetimos o processo, multiplicamos 8 por 2 e somamos com o terceiro coeficiente de P(x), o número 3. O cálculo é dado por 8.2 + 3 = 19. Escrevemos o resultado embaixo do coeficiente 3. Repetimos o procedimento pela última vez. Agora multiplicamos o 19 por 2 e somamos o resultado com – 1, ou seja, nós fazemos 19.2 + (– 1) = 37. O resultado 37 é colocado embaixo de –1 e é o resto de nossa divisão. =R(x) @hwurricane O polinômio resultante dessa divisão é determinado pelos números 5, 8 e 19. Estes são coeficientes desse polinômio. Como fora dito anteriormente, o último número (19) é acompanhado de x0, o 8 é acompanhado de x1, e o 5 é acompanhado de x2. Portanto, o polinômio resultante da divisão é 5x2 + 8x + 19, e o resto da divisão é r = 37. teorema de d'alembert é uma consequência imediata do teorema do resto, que são voltados para a divisão de polinômio por binômio do tipo x – a. O teorema do resto diz que um polinômio G(x) dividido por um binômio x – a terá resto R igual a P(a), para x = a. O matemático francês D’Alembert provou, levando em consideração o teorema citado acima, que um polinômio qualquer Q(x) será divisível por x – a, ou seja, o resto da divisão será igual à zero (R = 0) se P(a) = 0. Esse teorema facilitou o cálculo da divisão de polinômio por binômio (x –a), dessa forma não sendo preciso resolver toda a divisão para saber se o resto é igual ou diferente de zero. Exemplo 1 Calcule o resto da divisão (x² + 3x – 10) : (x – 3). Como diz o Teorema de D’Alembert, o resto (R) dessa divisão será igual a: P(3) = R 3² + 3 * 3 – 10 = R 9 + 9 – 10 = R 18 – 10 = R R = 8 Portanto, o resto dessa divisão será 8. Exemplo 2 Calcule o resto da divisão do polinômio 3x3 + x2 – 6x + 7 por 2x + 1. R = P(x) → R = P(– 1/2) R = 3*(–1/2)³ + (–1/2)² – 6*(–1/2) + 7 R = 3*(–1/8) + 1/4 + 3 + 7 R = –3/8 + 1/4 + 10 (mmc) R = –3/8 + 2/8 + 80/8 R = 79/8 raiz: Q(x) = 0 x – 3 = 0 x= 3 @hwurricane






