SUPERFÍCIES TOPOGRÁFICAS
• Definição: são superfícies que não podemos
representar por equações em virtude de sua forma
geometricamente indeterminada; relevo natural.
• Levantamento planimétrico: projeção plana que não
traz informações acerca do relevo do terreno levantado;
somente acerca de informações relativas à medições
feitas na horizontal.
• Levantamento altimétrico: projeção plana que traz
informações acerca do relevo do terreno levantado.
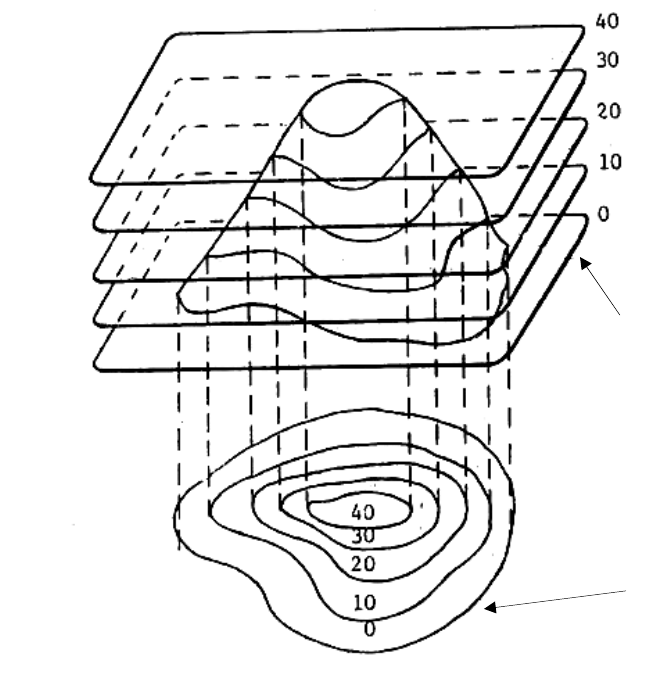
•Representação da superfície topográfica
•Curvas de nível: interseções da superfície topográfica
com os planos de nível dispostos a intervalos regulares.
planos e m nível
curvas de nív el
Interpretação de uma
planta topográfica 10 98
7
6
5
7
6
5
89
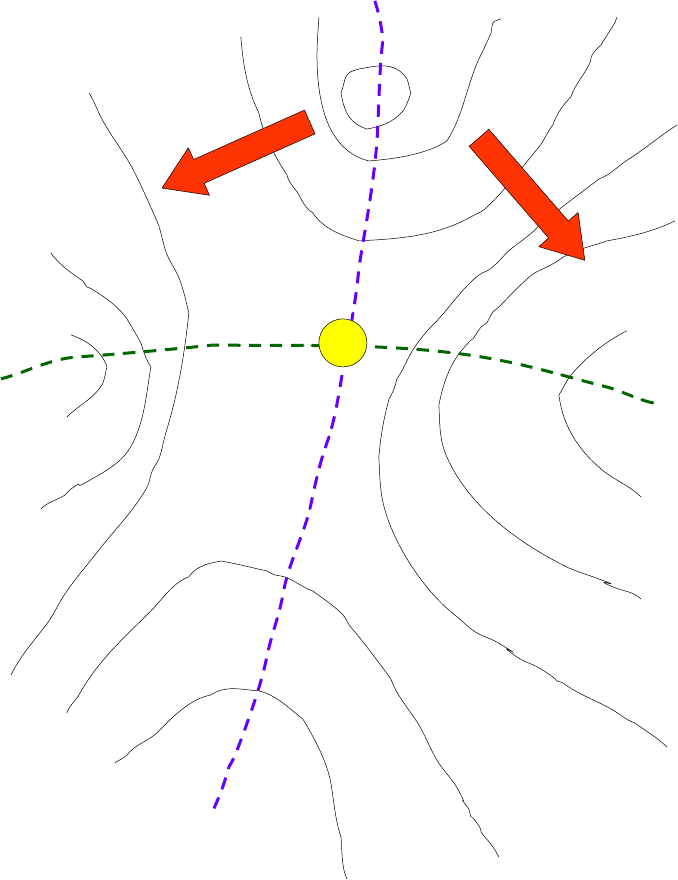
•Vertentes: superfícies laterais das
elevações ou depressões
•Linha de cumiada: linha comum
a duas vertentes ascendentes. Em
torno dela, curvas de cotas
menores envolvem curvas de cotas
maiores
•Talweg: linha comum a duas
vertentes descendentes. Em torno
dela, curvas de cotas maiores
envolvem curvas de cotas
menores.
•Garganta: ponto comum de uma
linha de cumiada com um talweg
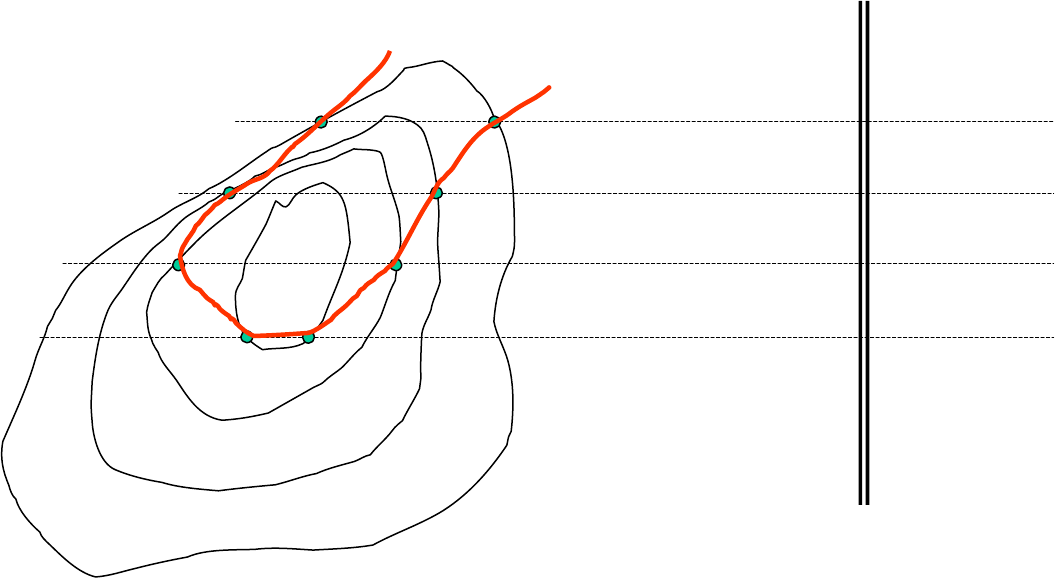
Interseção de um plano genérico com uma superfície
topográfica
70
60
50
40
70
60
50
40
A superfície topográfi ca é repres entada por suas curvas de nível
O plano genér ico é representad o por su a escala de decl ividade
Traça m-se plano s horizonta is (rep resentados por linhas trace jadas) a pa rtir da gr aduação do plano
genérico. As linhas t racejadas ser ão perpendicu lares à escala de dec lividade do p lano genéri co
Identif icam-se as inters eções entre os planos hori zontais auxil iares e as cu rvas de níve l
Ligam-se os pontos. Es tá traçada a in terseção desejada.

Perfis -
este é um caso específico do slide anterior, onde o
plano genérico é vertical.
Puxar linh as auxiliar es de inters eção entre o pl ano vertical e as curvas de nível
Desenhar linh as horizont ais que repr esentam os plan os horizonta is refer entes às curvas d e nível, na
mes ma escal a da planta to pográfica
Identif icar as inte rseções ent re as lin has auxilia res e os planos horizontais
Traçar a l inha que une as int erseções identifi cadas anter ior mente
0
5
10
15
20
25
30
Sejam dado s a planta a ltimét rica e o plan o vertical q ue a secciona rá
5
10 15
20
25
30
0
PLANO VERTICAL
Inclinação, declividade, intervalo
Todas estas três variáveis medem o grau de declividade de um talude, rampa ou plano
qualquer. A inclinação é dada em graus; a declividade é dada em percentual, e o
intervalo em cm, m ou km.
Inclinação (º) =  = arctg h/I … tg  = h/d
Declividade (%) = h/d = tg Â
Intervalo = 1/declividade, ou seja, d/h
a
h
dÂ
90º
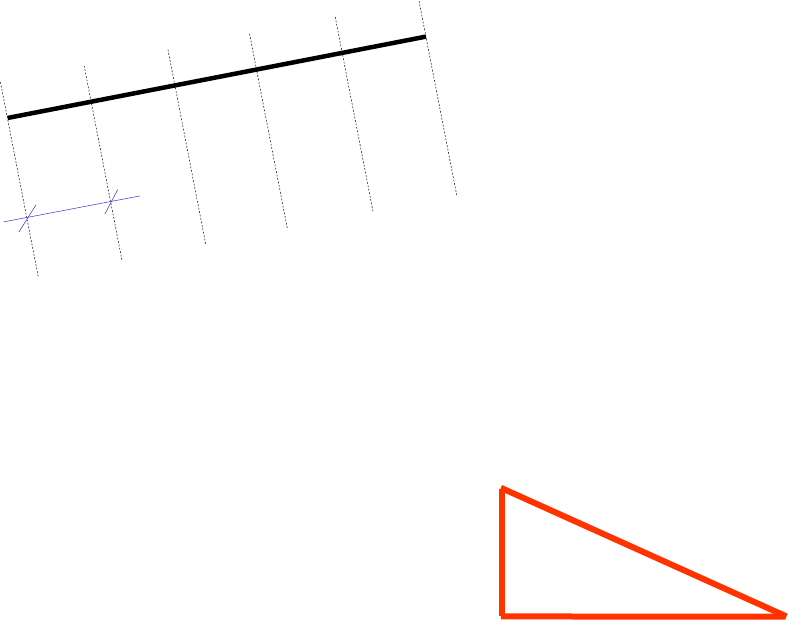
h = 11 - 6 = 5
o nú mero entre parênteses , que segue ao nome do pon to, indica a cota deste, ou seja, a altu ra
do ponto em relação ao plano do desen ho.
o desenho é uma projeção da reta, fei ta no plano do p apel.
d é medido di retamente em escala . no caso, d=5 c m
intervalo I = d/h = 5/(11-6 ) = 1 c m
Problema 1
Graduar a proj eção de u ma reta q ualquer,desenhad a na escala 1 /100, u ma vez con hecidos
dois de seus po ntos,
A(6)
B(11)
1 cm
78910
a
h
dÂ
90º
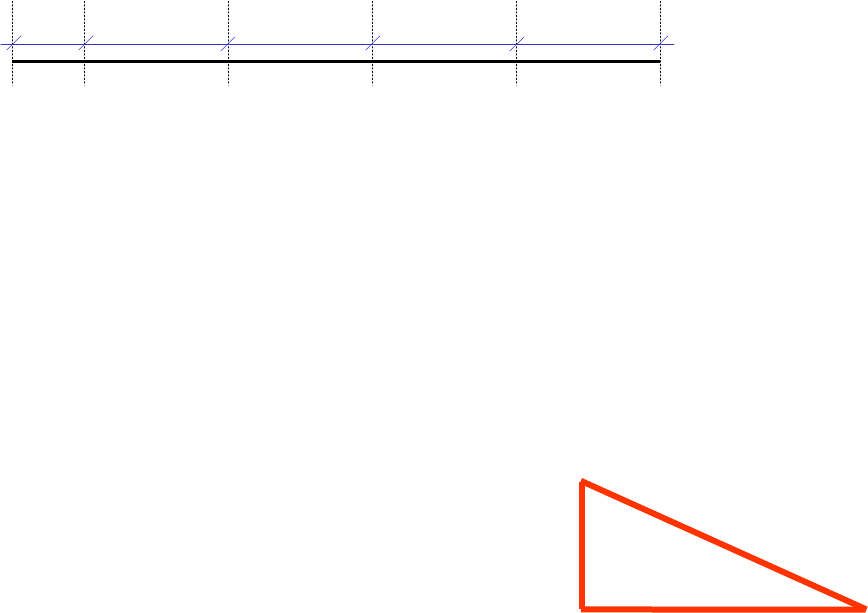
Neste caso, o primei ro intervalo da esquerda é d iferente dos demais, p or se trat ar de um inte rvalo
que comporta rá a metade das unidades dos outros. De 6 ,5 a 7 tere mos 5 mm, enqu anto nos
outros int ervalos t eremos 10 mm.
Mede-se a p rojeção da r eta = 5 cm. Depo is calclua-se a declividade dela. decl= (11-6,5)/5=90%
Para o pri meiro int ervalo, se decl=0 ,9 e h=0,5 (altur a entre 6,5 e 7 cm), pode mos faz er uma re gra
de 3:se a dec lividad e é de 90 cm para cada 100 cm, se rá de quanto para 0,5 c m? Respos ta: 0,55
cm, Este é o p rimeiro intervalo .
a
h
dÂ
90º
Para os de mais interva los, nova regr a de 3: se a
declivid ade é de 90 c m para cada 100 cm, será de qu anto
para 1 c m? Respo sta: 1,11 c m.
Problema 2
Graduar a proj eção de u ma reta q ualquer,desenhad a na escala 1 /100, u ma vez con hecidos
dois de seus po ntos.
A(6,5) B(11)
0,55 cm 1,11 cm 1,11 cm1,11 cm1,11 cm
789 10
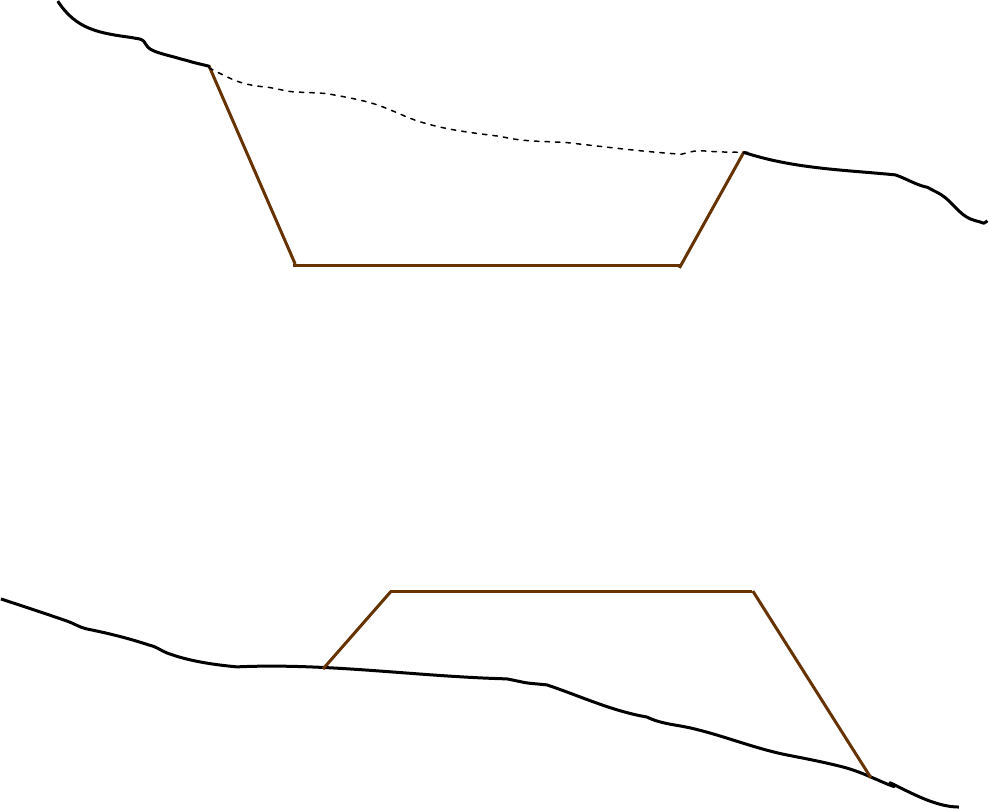
Cortes
offset
offset
platafo rma
pé pé
Aterros
platafo rma
offset
offset
talude
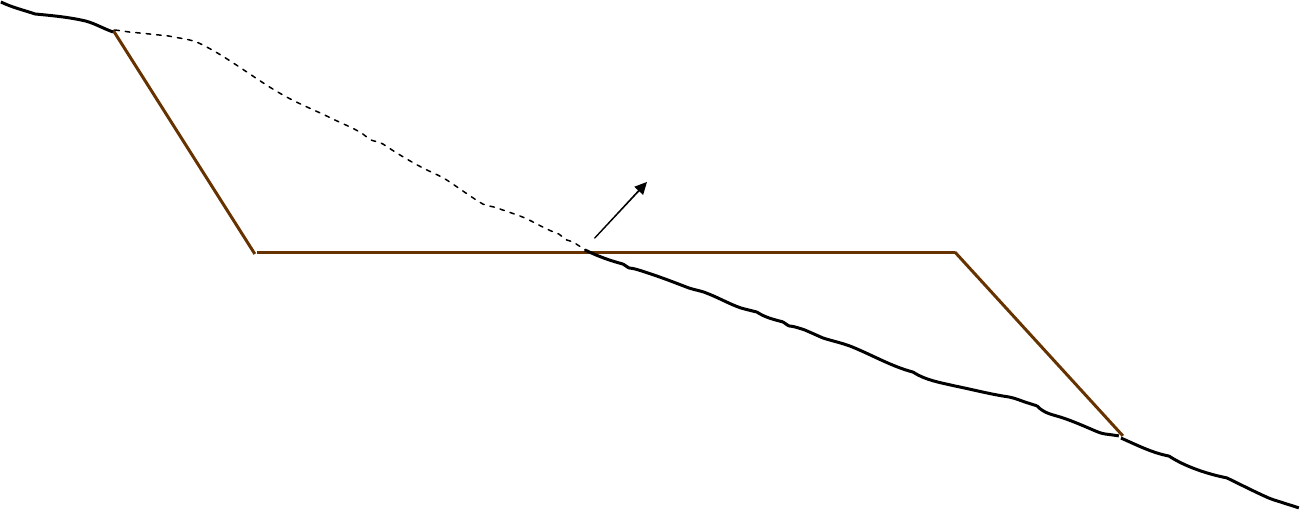
Seção mista
corte
aterro
offset
offset
ponto de p assagem
Prévia do material em texto
SUPERFÍCIES TOPOGRÁFICAS • Definição: são superfícies que não podemos representar por equações em virtude de sua forma geometricamente indeterminada; relevo natural. • Levantamento planimétrico: projeção plana que não traz informações acerca do relevo do terreno levantado; somente acerca de informações relativas à medições feitas na horizontal. • Levantamento altimétrico: projeção plana que traz informações acerca do relevo do terreno levantado. •Representação da superfície topográfica •Curvas de nível: interseções da superfície topográfica com os planos de nível dispostos a intervalos regulares. planos em nível curvas de nível Interpretação de uma planta topográfica 10 9 8 7 6 5 7 6 5 8 9 •Vertentes: superfícies laterais das elevações ou depressões •Linha de cumiada: linha comum a duas vertentes ascendentes. Em torno dela, curvas de cotas menores envolvem curvas de cotas maiores •Talweg: linha comum a duas vertentes descendentes. Em torno dela, curvas de cotas maiores envolvem curvas de cotas menores. •Garganta: ponto comum de uma linha de cumiada com um talweg Interseção de um plano genérico com uma superfície topográfica 70 60 50 40 70 60 50 40 A superfície topográfica é representada por suas curvas de nível O plano genérico é representado por sua escala de declividade Traçam-se planos horizontais (representados por linhas tracejadas) a partir da graduação do plano genérico. As linhas tracejadas serão perpendicularesà escala de declividade do plano genérico Identificam-se as interseções entre os planos horizontais auxiliares e as curvas de nível Ligam-se os pontos. Está traçada a interseção desejada. Perfis -este é um caso específico do slide anterior, onde o plano genérico é vertical. Puxar linhas auxiliares de interseção entre o plano vertical e as curvas de nível Desenhar linhas horizontais que representam os planos horizontais referentes às curvas de nível, na mesma escala da planta topográfica Identificar as interseções entre as linhas auxiliares e os planos horizontais Traçar a linha que une as interseções identificadas anteriormente 0 5 10 15 20 25 30 Sejam dados a planta altimétrica e o plano vertical que a seccionará 5 10 15 20 25 30 0 PLANO VERTICAL Inclinação, declividade, intervalo Todas estas três variáveis medem o grau de declividade de um talude, rampa ou plano qualquer. A inclinação é dada em graus; a declividade é dada em percentual, e o intervalo em cm, m ou km. Inclinação (º) =  = arctg h/I … tg  = h/d Declividade (%) = h/d = tg  Intervalo = 1/declividade, ou seja, d/h a h d  90º h = 11 - 6 = 5 o número entre parênteses, que segue ao nome do ponto, indica a cota deste, ou seja, a altura do ponto em relação ao plano do desenho. o desenho é uma projeção da reta, feita no plano do papel. d é medido diretamente em escala. no caso, d=5 cm intervalo I = d/h = 5/(11-6) = 1 cm Problema 1 Graduar a projeção de uma reta qualquer,desenhada na escala 1/100, uma vez conhecidos dois de seus pontos, A(6) B(11) 1 cm 7 8 9 10 ah d  90º Neste caso, o primeiro intervalo da esquerda é diferente dos demais, por se tratar de um intervalo que comportará a metade das unidades dos outros. De 6,5 a 7 teremos 5 mm, enquanto nos outros intervalos teremos 10 mm. Mede-se a projeção da reta = 5 cm. Depois calclua-se a declividade dela. decl=(11-6,5)/5=90% Para o primeiro intervalo, se decl=0,9 e h=0,5 (altura entre 6,5 e 7 cm), podemos fazer uma regra de 3:se a declividade é de 90 cm para cada 100 cm, será de quanto para 0,5 cm? Resposta: 0,55 cm, Este é o primeiro intervalo. ah d  90º Para os demais intervalos, nova regra de 3: se a declividade é de 90 cm para cada 100 cm, será de quanto para 1 cm? Resposta: 1,11 cm. Problema 2 Graduar a projeção de uma reta qualquer,desenhada na escala 1/100, uma vez conhecidos dois de seus pontos. A(6,5) B(11) 0,55 cm 1,11 cm 1,11 cm1,11 cm1,11 cm 7 8 9 10 Cortes offset offset plataforma pé pé Aterros plataforma offset offset talude Seção mista corte aterro offset offset ponto de passagem Problema 3 Determinar a linha de offset de uma barragem cuja plataforma é limitada pelas horizontais AB e CD de cota 40 e cujas rampas tem as seguintes inclinações: 45º à esquerda de AB e 60º à direita de CD. A B C D 40 39 38 38 39 40 Definição das curvas de nível do talude esquerdo A B C D 40 39 38 38 39 40 h I 45º 1 1 Talude da esquerda: inclinação = 45º h=I=1 cm intervalo = declividade = 1 cm B D 40 40 39 39 38 38 A C Desenho das curvas de nível e offset do talude esquerdo Definição das curvas de nível do talude direito A B C D 40 39 38 38 39 40 h I 60º 0.577 0.577 Talude da direita: inclinação = 60º = arctg h/I tg 60º = h/I 1.73 = h/I I = 1/1.73 = 0.577 B 40 40 39 39 38 38 A Desenho das curvas de nível e offset dos dois taludes C D 40 39 38 38 39 40 Problema 4 Dada a plataforma abaixo no nível 3, desenhar as linhas de offset de corte (decl = 50%) e de aterro (decl = 30%) 0 1 2 3 4 5 corte: decl = 50% I=2 cm aterro: decl = 30% I=3.33 cm 3.33 aterro corte ponto de passagem ponto de passagem 0 1 2 3 4 5 2 bissetriz bissetriz 0 1 2 3 4 5 Novo desenho das curvas de nível Bibliografia MORAES, Antônio C.B. Geometria Cotada: notas de aula. Belo Horizonte. [197-?] (apostila) MENEZES, Alexandre. Desenho projetivo. Belo Horizonte: Escola de Arquitetura UFMG. [200-?] (apostila).




