
b Unidades de medida ou sistemas de medida é um tema bastante presente em
concursos públicos e por isto é mais um dos assuntos tratados em nosso site.
Para podermos comp arar um valor com outro, util izamos uma grandeza predefinid a como
referência, grandeza esta chamada de unidade padrão.
As unidades de medida padrão que nós brasileiros utilizamos com maior frequencia são o
grama, o litro e o metro, assim como o metro quadrado e o metro cúbico.
Além destas também fazemos uso de outras unidades de medida para realizarmos, por
exemplo a medição de tempo, de temperatura ou de ângulo.
Dependendo da unidade de medida que estamos uti lizando, a unidade em si ou é muito
grande ou muito pequena, neste caso então utili zamos os seus múltiplos ou su bmúltiplos. O
grama geralmente é uma unidade muito pequena para o uso cotidiano, por isto em geral
utilizamos o quilograma, assim como em geral utilizamos o mililitro ao invés da própria
unidade litro, quando o assunto é bebidas por exemplo.
Múltiplos e Submúltiplos
Os múltiplos e submúltiplos mais frequentemente utilizados estão expostos na tabe la a
seguir:
Tabela de Múltiplos e Submúltiplos mais Utilizados
das Unidades de Medida
Múltiplos
Submúltiplos
múltiplo
sigla
relação com a unidade
submúltiplo
sigla
relação com a unidade
quilo
k
mil vezes a unidade
deci
d
décima parte da unidade
hecto
h
cem vezes a unidade
centi
c
centésima parte da unidade
deca
da
dez vezes a unidade
mili
m
milésima parte da unidade
Abaixo temos a tabela completa com todos os múltiplos e submúltiplos definidos:
Tabela Completa de Múltiplos e Submúltiplos das
Unidades de Medida
Múltiplos
Submúltiplos
múltiplo
sigla
fator multiplicador
submúltiplo
sigla
fator multiplicador
yotta
y
1 000 000 000 000 000 000 000 000
deci
d
01
zetta
Z
1 000 000 000 000 000 000 000
centi
c
0,01
exa
E
1 000 000 000 000 000 000
mili
m
0,001
peta
P
1 000 000 000 000 000
micro
µ
0,000 001
tera
T
1 000 000 000 000
nano
n
0,000 000 001
giga
G
1 000 000 000
pico
p
0,000 000 000 001
mega
M
1 000 000
femto
f
0,000 000 000 000 001
quilo
k
1 000
atto
a
0,000 000 000 000 000 001
hecto
h
100
zepto
z
0,000 000 000 000 000 000 001
deca
da
10
yocto
y
0,000 000 000 000 000 000 000 001
Utilização das Unidades de Medida
Quando estamos interessados em sabe r a quantidade de líquido que cabe em um recipie nte,
na verdade estamo s interessados em saber a sua capacidade. O volume i nterno de um
recipiente é chamado de capacidade. A unidade de me dida utilizada na medi ção de
capacidades é o litro.
Se estivéssemos i nteressados em sabe r o volume do recipiente em si, a unidade de medida
utilizada nesta medição seria o metro cúbico.
Para l adrilharmos um cômodo de uma casa, é necessário que saibamos a área deste
cômodo. Áreas são medidas em metros quadrados.
Para sabermos o comprimento de uma corda, é necessário que a me çamos. Nesta medição
a unidade de medida utilizada será o metro ou metro linear.
Se você for fazer uma saborosa torta de chocolate, p recisará co mprar cacau e o mesmo será
pesado para medirmos a massa desejada. A unidade de medida de massa é o grama.
Veja a tabela a seg uir na qual agrupamos estas principai s unidades de medida, seus
múltiplos e submúlti plos do Sistema Métrico Decimal, segundo o Sistema Internacional
de Unidades - SI:
Subconjunto de Unidades de Medida do Sistema
Métrico Decimal
Medida de
Grandez
a
Fato
r
Múltiplos
Unidade
Submúltiplos
Capacidade
Litro
10
kl
Hl
dal
l
dl
cl
Ml
Volume
Metro
Cúbico
1000
km3
hm3
dam3
m3
dm3
cm3
mm3
Área
Metro
Quadrad
o
100
km2
hm2
dam2
m2
dm2
cm2
mm2
Comprimen
to
Metro
10
km
Hm
dam
m
dm
cm
Mm
Massa
Grama
10
kg
Hg
dag
g
dg
cg
Mg
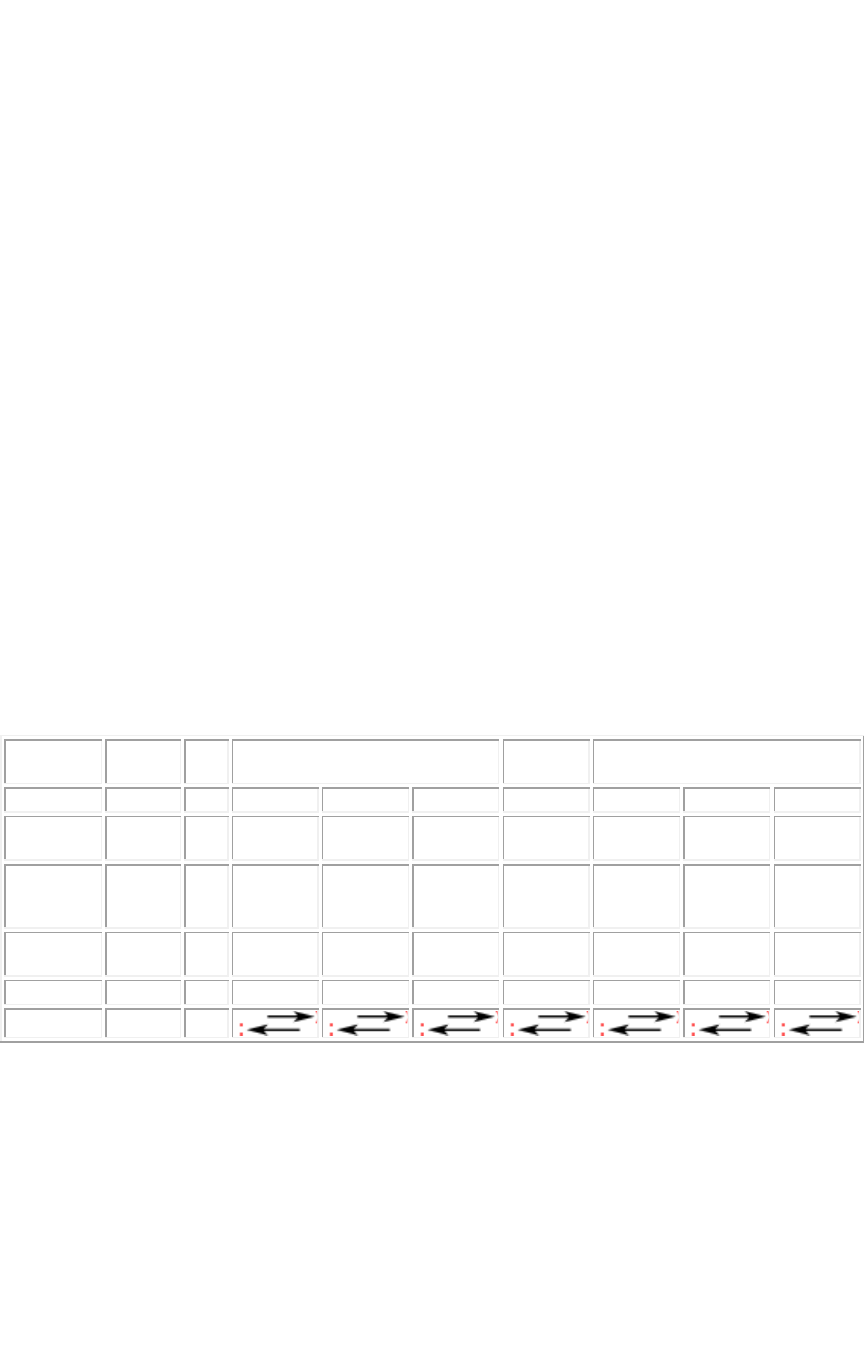
Observe que as set as que apo ntam para a di reita i ndicam uma mult iplicação pelo fator
multiplicador (10, 100 ou 10 00 dependendo da unidade de medi da), assim como as setas
que apontam para a esquerda indicam uma divisão também pelo fator.
A conversão de uma unidade p ara outra unidade dentro da me sma grandeza é reali zada
multiplicando-se ou dividindo -se o seu valor pelo fator de conversão, dependendo da unidade
original estar à esquerda ou à direita da unidade a que se pretende chegar, tanta s vezes
quantos forem o número de níveis de uma unidade a outra.
Exemplos de Conversão entre Unidades de Medida

Converta 2,5 metros em centí metros
Para convertermos 2,5 metros em centímetros, devemos multiplicar (porque na tabela
metro está à esquerda de centí metro) 2,5 por 10 duas vezes, pois para passarmos de
metros para centímetros sal tamos dois níveis à di reita. Primeiro passamos de metros
para decímetros e depois de decímetros para centímetros:
Isto equivale a passar a vírgula duas casas para a direita.
Portanto:
2,5 m é igual a 250 cm
Passe 5.200 gramas para quilogramas
Para passarmos 5.200 gramas para quilogramas , devemos dividir (porque n a tabel a
grama est á à direita de quilograma) 5.200 por 10 três vezes, po is p ara passarmos de
gramas para quilogramas saltamos três níveis à esquerda. Primeiro passamos d e grama
para decagrama, depois de decagrama para hectograma e finalmente de hectograma
para quilograma:
Isto equivale a passar a vírgula três casas para a esquerda.
Portanto:
5.200 g é igual a 5,2 kg
Quantos centilitros equivalem a 15 hl?
Para irmos de hectolitros a centil itros, passaremos quatro níveis à direi ta. Multi plicaremos
então 15 por 10 quatro vezes:
Isto equivale a passar a vírgula quatro casas para a direita.
Portanto:
150.000 cl equivalem a 15 hl.
Quantos quilômetros cúbicos equivalem a 14 mm3
?
Para passarmos de milí metros cúbicos p ara quilômetros cú bicos, passare mos seis níveis
à esquerda. Dividiremos então 14 por 1000 seis vezes:
Portanto:

0,000000000000000014 km 3, ou a 1,4 x 10 -17 km3 se express o em notação científ ica
equivalem a 14 mm3.
Passe 50 dm2
para hectometros quadrados
Para p assarmos de decímetros quadrados para hectometros quadrados , passaremos
três níveis à esquerda. Dividiremos então por 100 três vezes:
Isto equivale a passar a vírgula seis casas para a esquerda.
Portanto:
50 dm2 é igual a 0,00005 hm2
Equivalência en tre medidas de volume e
medidas de capacidade
Um cubo com aresta de 1 0 cm terá um vol ume de 1.000 cm3, medida esta equivalente a 1
l.
Como 1.000 cm3 equivalem a 1 dm3, temos que 1 dm3 equivale a 1 l.
Como um litro equivale a 1.000 ml, podemos afirmar que 1 cm3 equivale a 1 ml.
1.000 dm3 equivalem a 1 m3, portanto 1 m3 é equivalente a 1.000 l, que equivalem a 1 kl.
Exemplos de Conversão entre Medidas de Volume e
Medidas de Capacidade
Quantos decalitros equivalem a 1 m3?
Sabemos que 1 m3 equivale a 1.000 l, portanto para convertermos de l itros a decalitros,
passaremos um nível à esquerda. Dividiremos então 1.000 por 10 apenas uma vez:
Isto equivale a passar a vírgula uma casa para a esquerda.
Poderíamos também raciocinar da seguinte forma:
Como 1 m3 equi vale a 1 kl, basta fazermos a conversão de 1 kl para decalitros, quando
então passaremos dois níveis à direita. Multiplicaremos então 1 por 10 duas vezes:
Portanto:
100 dal equivalem a 1 m3.

348 mm3 equivalem a quantos decili tros?
Como 1 cm3 e quivale a 1 ml, é melhor dividirmos 348 mm3 po r mil, para o btermos o seu
equivalente em centimetros cúbicos: 0,348 cm3. Logo 348 mm3 equivale a 0,348 ml, já
que cm3 e ml se equivalem.
Neste ponto já co nvertemos de uma unidade de medida de volum e, para uma unidade de
medida de capacidade.
Falta-nos passarmos de mililitros para decilitros, qua ndo então passaremos do is níveis à
esquerda. Dividiremos então por 10 duas vezes:
Logo:
348 mm3 equivalem a 0,00348 dl.
Dúvidas Frequentes
Notei que com muita frequência esta página é acessada através do result ado de pesquisas
semelhantes a estas nos sites de buscas:
Um metro cúbico equivale a quantos metros quadrados?
Converter medidas em decilitros para gramas.
Quantos litros cabem em um metro quadrado?
Como passar litros para milímetros?
Quantos centímetros lineares há em um metro quadrado?
Conversão de litros para gramas.
Um centímetro corresponde a quantos litros?
Como passar de centímetros quadrados para mililitros?
Quantos mililitros tem um centímetro?
Transformar m3 em metro linear.
Quanto vale um centímetro cúbico em gramas?
Você consegue notar algum problema nestas pesquisas?
O prob lema é que elas buscam a conversão e ntre unidades de medidas incompatíveis, como
por exemplo, a conversão de metro cúbico para metro quadrado. A pri meira é uma u nidade
de medida de vol ume e a segunda é uma unidade de medida de área, por isto são
incompatíveis e não existe conversão de uma unidade para a outra.
Então to das as conversões acima n ão são po ssíveis de se realizar, a não que se tenha outras
informações, como a densidade do material na última questão, mas isto já uma outra
disciplina.
Acredito que a razão de stas dúvidas é o fato de o estudante não conseguir discernir
claramente o que são comprimento, área, volume e ca pacidade, por isto vou procurar
esclarecer tais conceitos com maiores detalhes.
Comprimento
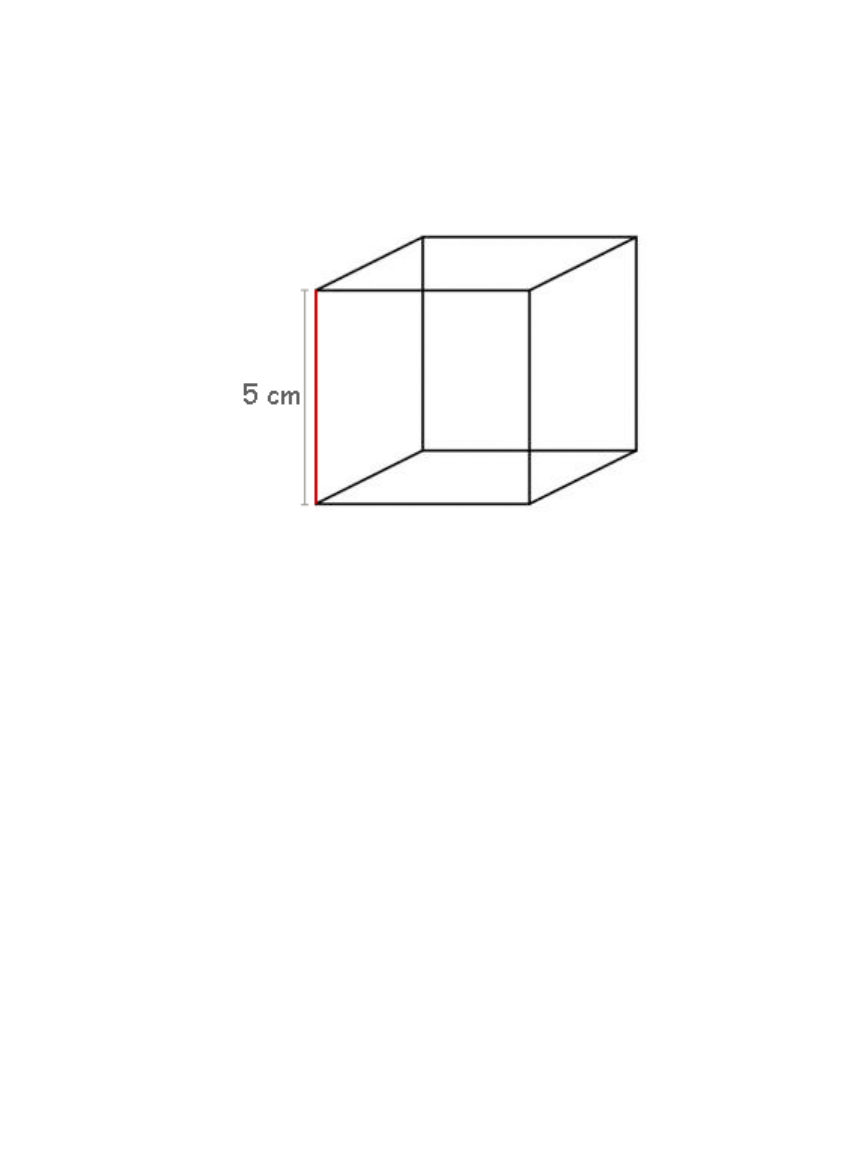
Vamos entender o que é uma medida de comprimento analisando o cubo ao lado.
Caso você não saiba o u n ão se lembre, as arest as d e um cubo são as linhas orig inadas pelo
encontro de suas faces.
Nosso cubo em estudo possui doze arestas, sendo onze pretas e uma vermelha.
Como todas as seis faces de um cubo são formadas p or quadrado s iguais, t odas as suas
arestas possuem o mesmo tamanho.
Pela fig ura identi ficamos que a aresta vermel ha, e também as demais, já que são todas
iguais, tem uma medida linear de 5 cm. Esta é a medida do seu comprimento.
Já que a aresta vermelha e sta na posição vertical, podemos uti lizá -la para medir a altura do
cubo, ou seja, ele mede 5 cm de altura.
Utilizamos med idas de comprimento para a medi ção de al turas, larguras, profundidades.
Como você pode not ar, todos est es exemplos tem apenas uma dimensão. A a resta do cubo
só tem uma dime nsão, você te m como medir o seu compri mento, mas não a sua espe ssura,
por exemplo.
Comprimentos são extensões unidimensionais.
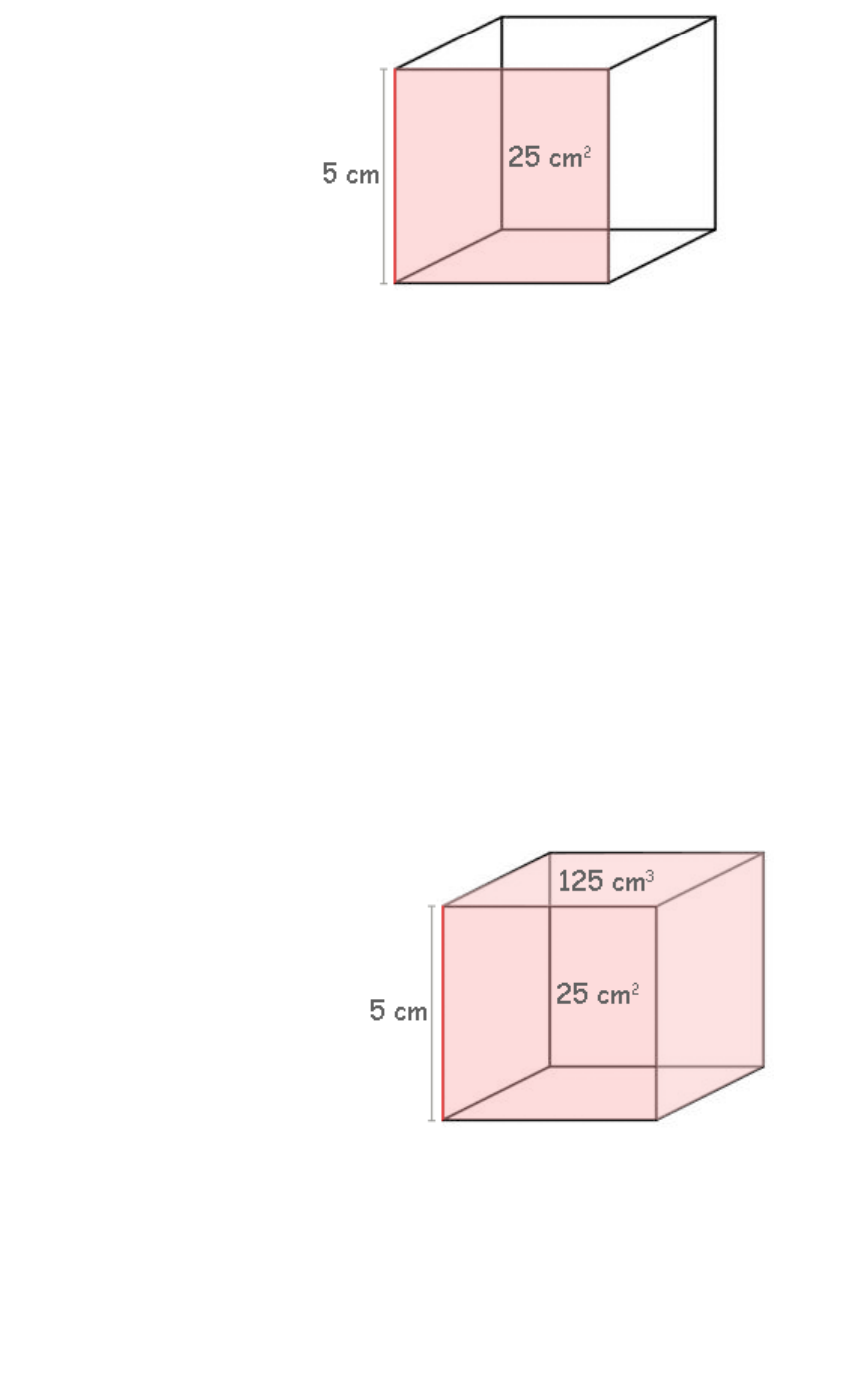
Área ou Superfície
Agora o nosso cubo tem a sua face frontal em rosa.
Qual é a superfície desta face?
Quando falamos em superfície estamos falando em área.
Áreas são extensões bidimensionais, pois como pod emos ver na figura, a face que
estamos anali sando possui uma altura de 5 cm e uma base, que po r se tratar de um cubo,
com a mesma medida.
Diferentemente da aresta que possui apenas uma dimensão, o seu comprimento, a área
das faces possui duas dimensões, altura e base, por exemplo.
Como este cubo t em uma arest a de 5 cm, a área das suas faces será igual a 5 cm . 5 c m
que é igual a (5 cm)2, igual a 52 cm2, ou seja, 25 cm2.
O expoente 2 do cm2 indica que esta é u ma unidade de medida com duas dimensões,
portanto não é uma unidade de medida linear que possui apenas uma dimensão.
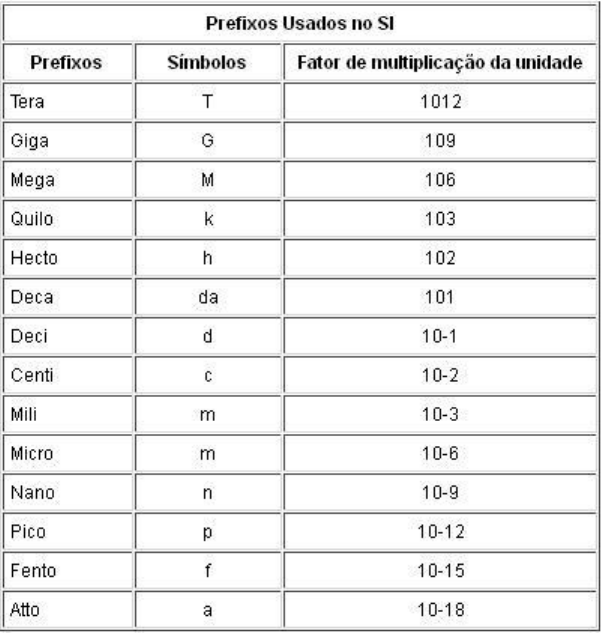
Volume e Capacidade
Agora cubo está todo em rosa.
Qual é o volume deste cubo?
O volume é o espaço ocu pado por um sóli do. No rmalmente para líquidos utilizamos o termo
capacidade.
Nosso cubo possui altura, largura e profundidade, portanto, possui três dimensões.

Volumes são extensões tridimensionais. O volume d o nosso cubo é obtid o através do
produto 5 cm . 5 cm . 5 cm que é igual a (5 cm)3, igual a 53 cm3 que resulta em 125 cm3.
O expoente 3 do cm3 nos diz que esta é uma unidade de medida com três dimensões,
portanto não é uma unidade de med ida linear que só possui uma dimensão, nem
bidimensional que só possui duas.
Como unidades de capaci dade também são unidades de vol ume, podemos estabelecer
relações como, por e xemplo, 1 cm3 equivale a 1 ml, o que nos p ermite transformações de
unidade de medida de volume em unidades de medida de capacidade e vice-versa.
Conversões entre unidades de diferentes dimensões não são possíveis, por isto as
conversões levantadas acima pelos internautas não são permitidas.
Unidades de Comprimento
A unidade de principal d e comprimento é o metro, entretanto existem situações em que
essa unidade deixa de ser prática. S e queremos medir grandes ex tensões ela é muito
pequena, por outro lado se queremos medir extensões muito "pequenas", a unidade
metro é muito "grande".
Os múltiplos e submúltiplos do metro são cha mados de unidades s ecundárias de
comprimento.
Na tabela abaixo vemos as unidades de co mprimento, seus símbolos e o valor
correspondente em metro. Na tabela, cada unidade de comprimento corresponde a 10
vezes a unidade da comprimento imediatamente inferior (à direita). Em conseqüência,
cada unidade de comprimento corresponde a 1 décimo da unidade i mediatamente
superior (à esquerda).
Quilômetro
km
Hectômetro
hm
Decâmetro
dam
Metro
m
Decímetro
dm
Centímetro
cm
Milímetro
mm
1000 m
100 m
10 m
1 m
0,1 m
0,01 m
0,001 m
Regras Práticas:
Para passar de uma unidade para outra imediatamente inferior devemos fazer uma
multiplicação por 10.
Ex : 1 m = 10 dm
Para passar de uma unidade para outra imediatamente superior, devemos fazer uma
divisão por 10.
Ex : 1 m = 0,1 dam
Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma
das regras anteriores.

Ex : 1 m = 100 cm
1 m = 0,001 km
Uidades de Área
Quilômeto
quadrado
km
2
Hectômetro
quadrado
hm
2
Decâmetro
quadrado
dam2
Metro
quadrado
m2
Decímetro
quadrado
dm
2
Centímetro
quadrado
cm
2
Milímetro
quadrado
mm2
1x106 m2
1x104 m2
1x102 m2
1 m2
1x10-2 m2
1x10-4 m2
1x10-6 m2
Regras Práticas:
Para passar de uma unidade para outra imediatamente inferior devemos fazer uma
multiplicação por 100.
Ex : 1 m2 = 100 dm2
Para passar de uma unidade para outra imediatamente superior, devmos fazer uma
divisão por 100.
Ex : 1 m2 = 0,01 dam2
Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma
das regras anteriores.
Uidades de Volume
Quilômetro
cúbico
km
3
Hectômetro
cúbico
hm
3
Decâmetro
cúbico
dam3
Metro
cúbico
m3
Decímetro
cúbico
dm
3
Centímetro
cúbico
cm
3
Milímetro
cúbico
mm3
1x109 m3
1x106 m3
1x103 m3
1 m3
1x10-3 m3
1x10-6 m3
1x10-9 m3
Regras Práticas:
Para passar de uma unidade para outra imediatamente inferior devemos fazer uma
multiplicação por 1000.
Ex : 1 m3 = 1000 dm3
Para passar de uma unidade para outra imediatamente superior, devemos fazer uma
divisão por 1000.
Ex : 1 m3 = 0,001 dam3
Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma
das regras anteriores.
Litro
O litro( l ) é uma medida de volume muito comum e que corresponde a 1 dm3.
1 litro = 0,001 m3 => 1 m3 = 1000 litros
1 litro = 1 dm3
1 litro = 1.000 cm3
1 litro = 1.000.000 mm3
Sistema Internacional de Unidades
O Sistema Internacional de Unidades é baseado em 6 unidades fundamentais. A unidade
fundamental de comprimento é o metro. Para cada unidade existem as unidades
secundárias, que são expressas através d a adição de um prefixo ao nome correspondente
à unidade principal, de acordo com a proporção da medida.
Veja também:
Unidades de medidas
Sistema métrico decimal
Grandezas Físicas
Prévia do material em texto
b Unidades de medida ou sistemas de medida é um tema bastante presente em concursos públicos e por isto é mais um dos assuntos tratados em nosso site. Para podermos comparar um valor com outro, utilizamos uma grandeza predefinida como referência, grandeza esta chamada de unidade padrão. As unidades de medida padrão que nós brasileiros utilizamos com maior frequencia são o grama, o litro e o metro, assim como o metro quadrado e o metro cúbico. Além destas também fazemos uso de outras unidades de medida para realizarmos, por exemplo a medição de tempo, de temperatura ou de ângulo. Dependendo da unidade de medida que estamos utilizando, a unidade em si ou é muito grande ou muito pequena, neste caso então utilizamos os seus múltiplos ou submúltiplos. O grama geralmente é uma unidade muito pequena para o uso cotidiano, por isto em geral utilizamos o quilograma, assim como em geral utilizamos o mililitro ao invés da própria unidade litro, quando o assunto é bebidas por exemplo. Múltiplos e Submúltiplos Os múltiplos e submúltiplos mais frequentemente utilizados estão expostos na tabela a seguir: Tabela de Múltiplos e Submúltiplos mais Utilizados das Unidades de Medida Múltiplos Submúltiplos múltiplo sigla relação com a unidade submúltiplo sigla relação com a unidade quilo k mil vezes a unidade deci d décima parte da unidade hecto h cem vezes a unidade centi c centésima parte da unidade deca da dez vezes a unidade mili m milésima parte da unidade Abaixo temos a tabela completa com todos os múltiplos e submúltiplos definidos: Tabela Completa de Múltiplos e Submúltiplos das Unidades de Medida Múltiplos Submúltiplos múltiplo sigla fator multiplicador submúltiplo sigla fator multiplicador yotta y 1 000 000 000 000 000 000 000 000 deci d 01 zetta Z 1 000 000 000 000 000 000 000 centi c 0,01 exa E 1 000 000 000 000 000 000 mili m 0,001 peta P 1 000 000 000 000 000 micro µ 0,000 001 tera T 1 000 000 000 000 nano n 0,000 000 001 giga G 1 000 000 000 pico p 0,000 000 000 001 mega M 1 000 000 femto f 0,000 000 000 000 001 quilo k 1 000 atto a 0,000 000 000 000 000 001 hecto h 100 zepto z 0,000 000 000 000 000 000 001 deca da 10 yocto y 0,000 000 000 000 000 000 000 001 Utilização das Unidades de Medida Quando estamos interessados em saber a quantidade de líquido que cabe em um recipiente, na verdade estamos interessados em saber a sua capacidade. O volume interno de um recipiente é chamado de capacidade. A unidade de medida utilizada na medição de capacidades é o litro. Se estivéssemos interessados em saber o volume do recipiente em si, a unidade de medida utilizada nesta medição seria o metro cúbico. Para ladrilharmos um cômodo de uma casa, é necessário que saibamos a área deste cômodo. Áreas são medidas em metros quadrados. Para sabermos o comprimento de uma corda, é necessário que a meçamos. Nesta medição a unidade de medida utilizada será o metro ou metro linear. Se você for fazer uma saborosa torta de chocolate, precisará comprar cacau e o mesmo será pesado para medirmos a massa desejada. A unidade de medida de massa é o grama. Veja a tabela a seguir na qual agrupamos estas principais unidades de medida, seus múltiplos e submúltiplos do Sistema Métrico Decimal, segundo o Sistema Internacional de Unidades - SI: Subconjunto de Unidades de Medida do Sistema Métrico Decimal Medida de Grandez a Fato r Múltiplos Unidade Submúltiplos Capacidade Litro 10 kl Hl dal l dl cl Ml Volume Metro Cúbico 1000 km3 hm3 dam3 m3 dm3 cm3 mm3 Área Metro Quadrad o 100 km2 hm2 dam2 m2 dm2 cm2 mm2 Comprimen to Metro 10 km Hm dam m dm cm Mm Massa Grama 10 kg Hg dag g dg cg Mg Observe que as setas que apontam para a direita indicam uma multiplicação pelo fator multiplicador (10, 100 ou 1000 dependendo da unidade de medida), assim como as setas que apontam para a esquerda indicam uma divisão também pelo fator. A conversão de uma unidade para outra unidade dentro da mesma grandeza é realizada multiplicando-se ou dividindo-se o seu valor pelo fator de conversão, dependendo da unidade original estar à esquerda ou à direita da unidade a que se pretende chegar, tantas vezes quantos forem o número de níveis de uma unidade a outra. Exemplos de Conversão entre Unidades de Medida Converta 2,5 metros em centímetros Para convertermos 2,5 metros em centímetros, devemos multiplicar (porque na tabela metro está à esquerda de centímetro) 2,5 por 10 duas vezes, pois para passarmos de metros para centímetros saltamos dois níveis à direita. Primeiro passamos de metros para decímetros e depois de decímetros para centímetros: Isto equivale a passar a vírgula duas casas para a direita. Portanto: 2,5 m é igual a 250 cm Passe 5.200 gramas para quilogramas Para passarmos 5.200 gramas para quilogramas, devemos dividir (porque na tabela grama está à direita de quilograma) 5.200 por 10 três vezes, pois para passarmos de gramas para quilogramas saltamos três níveis à esquerda. Primeiro passamos de grama para decagrama, depois de decagrama para hectograma e finalmente de hectograma para quilograma: Isto equivale a passar a vírgula três casas para a esquerda. Portanto: 5.200 g é igual a 5,2 kg Quantos centilitros equivalem a 15 hl? Para irmos de hectolitros a centilitros, passaremos quatro níveis à direita. Multiplicaremos então 15 por 10 quatro vezes: Isto equivale a passar a vírgula quatro casas para a direita. Portanto: 150.000 cl equivalem a 15 hl. Quantos quilômetros cúbicos equivalem a 14 mm3? Para passarmos de milímetros cúbicos para quilômetros cúbicos, passaremos seis níveis à esquerda. Dividiremos então 14 por 1000 seis vezes: Portanto: 0,000000000000000014 km3, ou a 1,4 x 10-17 km3 se expresso em notação científica equivalem a 14 mm3. Passe 50 dm2 para hectometros quadrados Para passarmos de decímetros quadrados para hectometros quadrados, passaremos três níveis à esquerda. Dividiremos então por 100 três vezes: Isto equivale a passar a vírgula seis casas para a esquerda. Portanto: 50 dm2 é igual a 0,00005 hm2 Equivalência entre medidas de volume e medidas de capacidade Um cubo com aresta de 10 cm terá um volume de 1.000 cm3, medida esta equivalente a 1 l. Como 1.000 cm3 equivalem a 1 dm3, temos que 1 dm3 equivale a 1 l. Como um litro equivale a 1.000 ml, podemos afirmar que 1 cm3 equivale a 1 ml. 1.000 dm3 equivalem a 1 m3, portanto 1 m3 é equivalente a 1.000 l, que equivalem a 1 kl. Exemplos de Conversão entre Medidas de Volume e Medidas de Capacidade Quantos decalitros equivalem a 1 m3? Sabemos que 1 m3 equivale a 1.000 l, portanto para convertermos de litros a decalitros, passaremos um nível à esquerda. Dividiremos então 1.000 por 10 apenas uma vez: Isto equivale a passar a vírgula uma casa para a esquerda. Poderíamos também raciocinar da seguinte forma: Como 1 m3 equivale a 1 kl, basta fazermos a conversão de 1 kl para decalitros, quando então passaremos dois níveis à direita. Multiplicaremos então 1 por 10 duas vezes: Portanto: 100 dal equivalem a 1 m3. 348 mm3 equivalem a quantos decilitros? Como 1 cm3 equivale a 1 ml, é melhor dividirmos 348 mm3 por mil, para obtermos o seu equivalente em centimetros cúbicos: 0,348 cm3. Logo 348 mm3 equivale a 0,348 ml, já que cm3 e ml se equivalem. Neste ponto já convertemos de uma unidade de medida de volume, para uma unidade de medida de capacidade. Falta-nos passarmos de mililitros para decilitros, quando então passaremos dois níveis à esquerda. Dividiremos então por 10 duas vezes: Logo: 348 mm3 equivalem a 0,00348 dl. Dúvidas Frequentes Notei que com muita frequência esta página é acessada através do resultado de pesquisas semelhantes a estas nos sites de buscas: Um metro cúbico equivale a quantosmetros quadrados? Converter medidas em decilitros para gramas. Quantos litros cabem em um metro quadrado? Como passar litros para milímetros? Quantos centímetros lineares há em um metro quadrado? Conversão de litros para gramas. Um centímetro corresponde a quantos litros? Como passar de centímetros quadrados para mililitros? Quantos mililitros tem um centímetro? Transformar m3 em metro linear. Quanto vale um centímetro cúbico em gramas? Você consegue notar algum problema nestas pesquisas? O problema é que elas buscam a conversão entre unidades de medidas incompatíveis, como por exemplo, a conversão de metro cúbico para metro quadrado. A primeira é uma unidade de medida de volume e a segunda é uma unidade de medida de área, por isto são incompatíveis e não existe conversão de uma unidade para a outra. Então todas as conversões acima não são possíveis de se realizar, a não que se tenha outras informações, como a densidade do material na última questão, mas isto já uma outra disciplina. Acredito que a razão destas dúvidas é o fato de o estudante não conseguir discernir claramente o que são comprimento, área, volume e capacidade, por isto vou procurar esclarecer tais conceitos com maiores detalhes. Comprimento Vamos entender o que é uma medida de comprimento analisando o cubo ao lado. Caso você não saiba ou não se lembre, as arestas de um cubo são as linhas originadas pelo encontro de suas faces. Nosso cubo em estudo possui doze arestas, sendo onze pretas e uma vermelha. Como todas as seis faces de um cubo são formadas por quadrados iguais, todas as suas arestas possuem o mesmo tamanho. Pela figura identificamos que a aresta vermelha, e também as demais, já que são todas iguais, tem uma medida linear de 5 cm. Esta é a medida do seu comprimento. Já que a aresta vermelha esta na posição vertical, podemos utilizá-la para medir a altura do cubo, ou seja, ele mede 5 cm de altura. Utilizamos medidas de comprimento para a medição de alturas, larguras, profundidades. Como você pode notar, todos estes exemplos tem apenas uma dimensão. A aresta do cubo só tem uma dimensão, você tem como medir o seu comprimento, mas não a sua espessura, por exemplo. Comprimentos são extensões unidimensionais. Área ou Superfície Agora o nosso cubo tem a sua face frontal em rosa. Qual é a superfície desta face? Quando falamos em superfície estamos falando em área. Áreas são extensões bidimensionais, pois como podemos ver na figura, a face que estamos analisando possui uma altura de 5 cm e uma base, que por se tratar de um cubo, com a mesma medida. Diferentemente da aresta que possui apenas uma dimensão, o seu comprimento, a área das faces possui duas dimensões, altura e base, por exemplo. Como este cubo tem uma aresta de 5 cm, a área das suas faces será igual a 5 cm . 5 cm que é igual a (5 cm)2, igual a 52 cm2, ou seja, 25 cm2. O expoente 2 do cm2 indica que esta é uma unidade de medida com duas dimensões, portanto não é uma unidade de medida linear que possui apenas uma dimensão. Volume e Capacidade Agora cubo está todo em rosa. Qual é o volume deste cubo? O volume é o espaço ocupado por um sólido. Normalmente para líquidos utilizamos o termo capacidade. Nosso cubo possui altura, largura e profundidade, portanto, possui três dimensões. Volumes são extensões tridimensionais. O volume do nosso cubo é obtido através do produto 5 cm . 5 cm . 5 cm que é igual a (5 cm)3, igual a 53 cm3 que resulta em 125 cm3. O expoente 3 do cm3 nos diz que esta é uma unidade de medida com três dimensões, portanto não é uma unidade de medida linear que só possui uma dimensão, nem bidimensional que só possui duas. Como unidades de capacidade também são unidades de volume, podemos estabelecer relações como, por exemplo, 1 cm3 equivale a 1 ml, o que nos permite transformações de unidade de medida de volume em unidades de medida de capacidade e vice-versa. Conversões entre unidades de diferentes dimensões não são possíveis, por isto as conversões levantadas acima pelos internautas não são permitidas. Unidades de Comprimento A unidade de principal de comprimento é o metro, entretanto existem situações em que essa unidade deixa de ser prática. Se queremos medir grandes extensões ela é muito pequena, por outro lado se queremos medir extensões muito "pequenas", a unidade metro é muito "grande". Os múltiplos e submúltiplos do metro são chamados de unidades secundárias de comprimento. Na tabela abaixo vemos as unidades de comprimento, seus símbolos e o valor correspondente em metro. Na tabela, cada unidade de comprimento corresponde a 10 vezes a unidade da comprimento imediatamente inferior (à direita). Em conseqüência, cada unidade de comprimento corresponde a 1 décimo da unidade imediatamente superior (à esquerda). Quilômetro km Hectômetro hm Decâmetro dam Metro m Decímetro dm Centímetro cm Milímetro mm 1000 m 100 m 10 m 1 m 0,1 m 0,01 m 0,001 m Regras Práticas: Para passar de uma unidade para outra imediatamente inferior devemos fazer uma multiplicação por 10. Ex : 1 m = 10 dm Para passar de uma unidade para outra imediatamente superior, devemos fazer uma divisão por 10. Ex : 1 m = 0,1 dam Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma das regras anteriores. Ex : 1 m = 100 cm 1 m = 0,001 km Uidades de Área Quilômeto quadrado km2 Hectômetro quadrado hm2 Decâmetro quadrado dam2 Metro quadrado m2 Decímetro quadrado dm2 Centímetro quadrado cm2 Milímetro quadrado mm2 1x106 m2 1x104 m2 1x102 m2 1 m2 1x10-2 m2 1x10-4 m2 1x10-6 m2 Regras Práticas: Para passar de uma unidade para outra imediatamente inferior devemos fazer uma multiplicação por 100. Ex : 1 m2 = 100 dm2 Para passar de uma unidade para outra imediatamente superior, devmos fazer uma divisão por 100. Ex : 1 m2 = 0,01 dam2 Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma das regras anteriores. Uidades de Volume Quilômetro cúbico km3 Hectômetro cúbico hm3 Decâmetro cúbico dam3 Metro cúbico m3 Decímetro cúbico dm3 Centímetro cúbico cm3 Milímetro cúbico mm3 1x109 m3 1x106 m3 1x103 m3 1 m3 1x10-3 m3 1x10-6 m3 1x10-9 m3 Regras Práticas: Para passar de uma unidade para outra imediatamente inferior devemos fazer uma multiplicação por 1000. Ex : 1 m3 = 1000 dm3 Para passar de uma unidade para outra imediatamente superior, devemos fazer uma divisão por 1000. Ex : 1 m3 = 0,001 dam3 Para passar de uma unidade para outra qualquer, basta aplicar sucessivas vezes uma das regras anteriores. Litro O litro( l ) é uma medida de volume muito comum e que corresponde a 1 dm3. 1 litro = 0,001 m3 => 1 m3 = 1000 litros 1 litro = 1 dm3 1 litro = 1.000 cm3 1 litro = 1.000.000 mm3 Sistema Internacional de Unidades O Sistema Internacional de Unidades é baseado em 6 unidades fundamentais. A unidade fundamental de comprimento é o metro. Para cada unidade existem as unidades secundárias, que são expressas através da adição de um prefixo ao nome correspondente à unidade principal, de acordo com a proporção da medida. Veja também: Unidades de medidas Sistema métrico decimal Grandezas Físicas http://www.coladaweb.com/fisica/fisica-geral/unidades-de-medidas-e-principais-grandezas http://www.coladaweb.com/fisica/fisica-geral/unidades-de-medidas-e-principais-grandezas http://www.coladaweb.com/matematica/sistema-metrico-decimal http://www.coladaweb.com/fisica/fisica-geral/grandezas-fisicas


